T-score против z-score: когда их использовать?
Два термина, которые часто сбивают с толку студентов на курсах статистики, — это t-показатели и z-показатели .
Оба широко используются при проверке гипотез или построении доверительных интервалов , но они немного отличаются.
Вот формула для каждого:
оценка t = ( x – µ) / (s/√ n )
Золото:
- x : образец означает
- μ : Среднее число населения
- s : Выборочное стандартное отклонение
- n : Размер выборки
z-показатель = ( x – µ) / σ
Золото:
- x : значение необработанных данных
- μ : Среднее число населения
- σ : Стандартное отклонение генеральной совокупности.
На этой блок-схеме показано, когда вам следует использовать каждый из них, исходя из ваших данных:
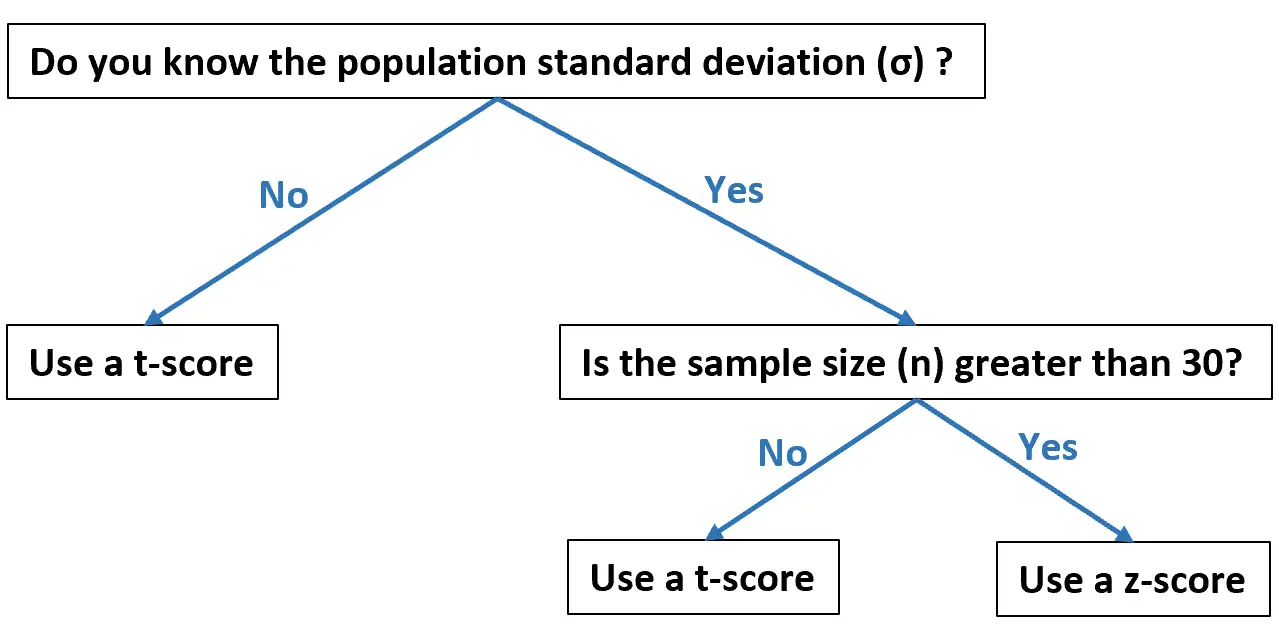
Следующие примеры показывают, как на практике рассчитать T-показатель и Z-показатель.
Пример 1: Расчет T-показателя
Предположим, ресторан готовит гамбургеры, утверждая, что их средний вес равен 0,25 фунта.
Предположим, мы берем случайную выборку из n = 20 гамбургеров и обнаруживаем, что средний вес выборки составляет x = 0,22 фунта со стандартным отклонением s = 0,05 фунта. Проведите проверку гипотезы, чтобы определить, равен ли фактический средний вес всех гамбургеров, произведенных в этом ресторане, 0,25 фунта.
В этом примере мы бы использовали T-показатель для проверки гипотезы, поскольку ни одно из следующих двух условий не выполнено.
- Стандартное отклонение генеральной совокупности (σ) известно. (σ не указано в этом примере)
- Размер выборки больше 30 (в данном примере n=20).
Итак, мы могли бы рассчитать t-показатель следующим образом:
- оценка t = ( x – µ) / (s/√ n )
- t-показатель = (0,22 – 0,25) / (0,05 / √ 20 )
- t-показатель = -2,68
Согласно калькулятору P-value T-score , значение p, соответствующее этому t-показателю, составляет 0,01481 .
Поскольку это значение p меньше 0,05, у нас есть достаточно оснований утверждать, что средний вес гамбургеров, приготовленных в этом ресторане, не равен 0,25 фунта.
Пример 2: Расчет показателя Z
Предположим, что компания производит батареи, срок службы которых, как известно, подчиняется нормальному распределению со средним значением μ = 20 часов и стандартным отклонением σ = 5 часов.
Предположим, мы взяли случайную выборку из n = 50 батарей и обнаружили, что среднее значение выборки составляет x = 21 час. Проведите проверку гипотезы, чтобы определить, равен ли истинный средний срок службы всех аккумуляторов, производимых этой компанией, 20 часам.
В этом примере мы бы использовали z-показатель для проверки гипотезы, поскольку выполняются оба следующих условия:
- Стандартное отклонение генеральной совокупности (σ) известно. (в этом примере σ равно 5)
- Размер выборки больше 30 (в данном примере n=50).
Итак, мы рассчитаем z-показатель следующим образом:
- z-показатель = ( x – µ) / σ
- z-оценка = (21 – 20) / 5
- z-оценка = 0,2
Согласно калькулятору Z-показателя P-значения, значение p, соответствующее этому z-показателю, составляет 0,84184 .
Поскольку это значение p не менее 0,05, у нас нет достаточных оснований утверждать, что средний срок службы всех аккумуляторов, производимых этой компанией, отличается от 20 часов.
Дополнительные ресурсы
Следующие учебные пособия содержат дополнительную информацию о показателях T и Z:
Нормальное распределение и t-распределение: в чем разница?
Как читать таблицу распределения t
Как читать таблицу Z