Понимание t-теста в линейной регрессии

Линейная регрессия используется для количественной оценки взаимосвязи между переменной-предиктором и переменной ответа.

Всякий раз, когда мы выполняем линейную регрессию, мы хотим знать, существует ли статистически значимая связь между переменной-предиктором и переменной ответа.

Мы проверяем значимость, выполняя t-тест для наклона регрессии. Для этого t-теста мы используем следующую нулевую и альтернативную гипотезу:

• H ₀ : β ₁ = 0 (наклон равен нулю)
• H _A : β ₁ ≠ 0 (наклон не равен нулю)

Затем мы вычисляем статистику теста следующим образом:

т = б /ЮВ _б

Золото:

• б : оценка коэффициента
• SE _b : стандартная ошибка оценки коэффициента.

Если значение p, соответствующее t , ниже определенного порога (например, α = 0,05), то мы отвергаем нулевую гипотезу и заключаем, что существует статистически значимая связь между переменной-предиктором и переменной ответа.

В следующем примере показано, как на практике выполнить t-тест для модели линейной регрессии.

Пример: выполнение t-теста для линейной регрессии

Предположим, профессор хочет проанализировать взаимосвязь между учебными часами и оценками на экзаменах 40 своих студентов.

Он выполняет простую линейную регрессию, используя часы обучения в качестве предикторной переменной и полученные баллы на экзаменах в качестве переменной ответа.

В следующей таблице показаны результаты регрессионной модели:

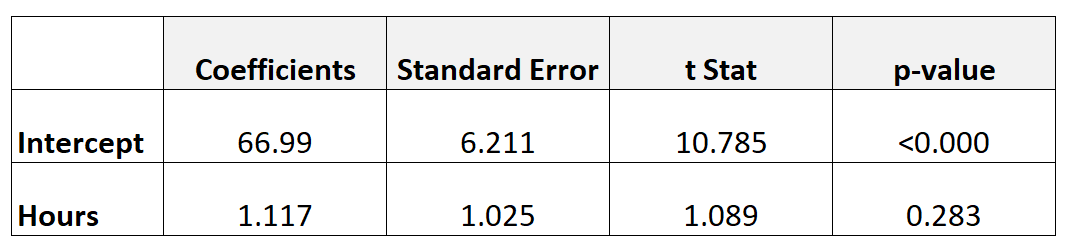
Чтобы определить, имеют ли изученные часы статистически значимую связь с оценкой на итоговом экзамене, мы можем провести t-критерий.

Для этого t-теста мы используем следующую нулевую и альтернативную гипотезу:

• H ₀ : β ₁ = 0 (наклон изучаемых часов равен нулю)
• H _A : β ₁ ≠ 0 (наклон изучаемых часов не равен нулю)

Затем мы вычисляем статистику теста следующим образом:

• т = б /ЮВ _б
• т = 1,117/1,025
• т = 1,089

Значение p, соответствующее t = 1,089 с df = n-2 = 40 – 2 = 38, составляет 0,283 .

Обратите внимание, что мы также можем использовать калькулятор T-оценки для значения P , чтобы вычислить это значение p:

Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.

Это означает, что изученные часы не имеют статистически значимой связи между результатами итогового экзамена.

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о линейной регрессии:

Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как интерпретировать коэффициенты регрессии
Как интерпретировать тест F для определения общей значимости регрессии