Как выполнить t-тест с неравными размерами выборки
Когда речь идет о статистике, студенты часто задают следующий вопрос:
Можно ли провести t-критерий, если размеры выборки в каждой группе не равны?
Короткий ответ:
Да, вы можете выполнить t-тест, если размеры выборки не равны. Равные размеры выборки не являются одним из допущений, сделанных в t-критерии.
Настоящие проблемы возникают, когда две выборки не имеют равных дисперсий, что является одним из допущений, сделанных в t-тесте.
В этом случае вместо этого рекомендуется использовать t-критерий Уэлча , который не предполагает равные дисперсии.
В следующих примерах показано, как выполнять T-тесты с неравными размерами выборок, когда дисперсии равны, а когда нет.
Пример 1: Неравные размеры выборки и равные дисперсии
Предположим, мы администрируем две программы, призванные помочь студентам лучше сдать определенные экзамены.
Результаты приведены ниже:
Программа 1:
- n (размер выборки): 500
- х (среднее выборочное): 80
- s (выборочное стандартное отклонение): 5
Программа 2:
- n (размер выборки): 20
- х (среднее выборочное): 85
- s (выборочное стандартное отклонение): 5
Следующий код показывает, как создать коробчатую диаграмму в R для визуализации распределения баллов экзамена для каждой программы:
#make this example reproducible set. seeds (1) #create vectors to hold exam scores program1 <- rnorm(500, mean=80, sd=5) program2 <- rnorm(20, mean=85, sd=5) #create boxplots to visualize distribution of exam scores boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))
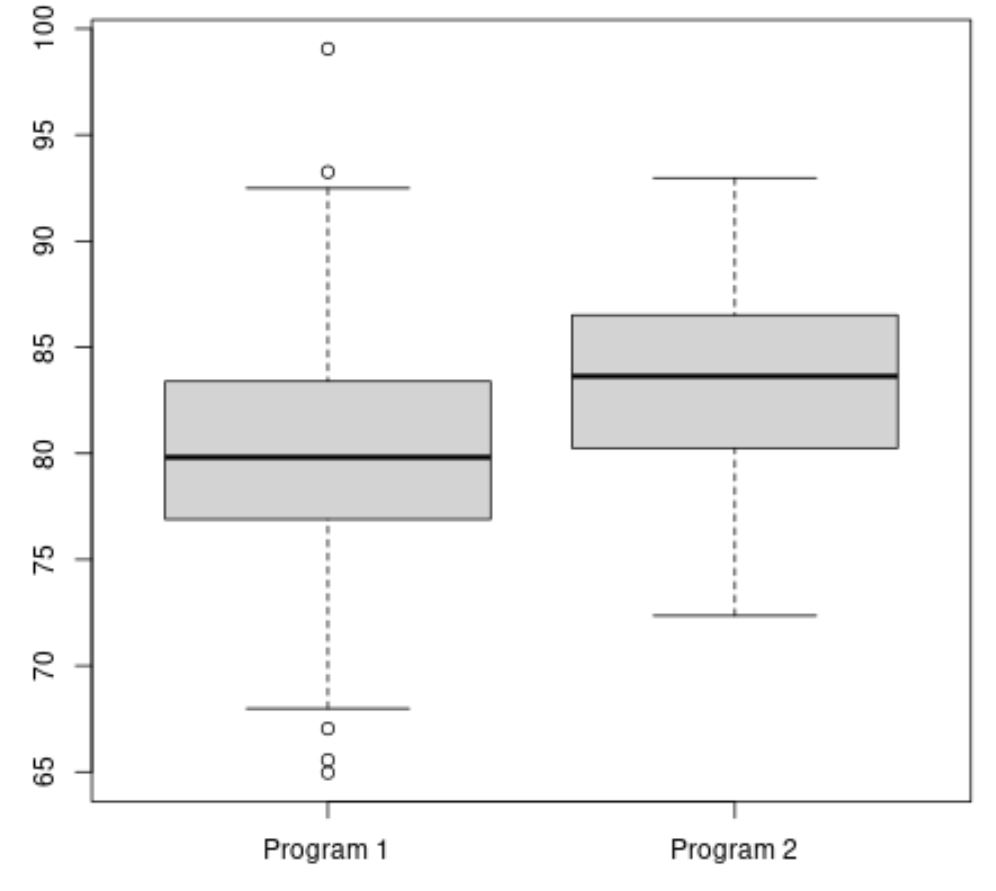
Средний балл экзамена по программе 2 кажется выше, но разница в баллах экзамена между двумя программами примерно одинакова.
Следующий код показывает, как выполнить t-критерий независимых выборок с помощью t-критерия Уэлча:
#perform independent samples t-test t. test (program1, program2, var. equal = TRUE ) Two Sample t-test data: program1 and program2 t = -3.3348, df = 518, p-value = 0.0009148 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.111504 -1.580245 sample estimates: mean of x mean of y 80.11322 83.95910 #perform Welch's two sample t-test t. test (program1, program2, var. equal = FALSE ) Welch Two Sample t-test data: program1 and program2 t = -3.3735, df = 20.589, p-value = 0.00293 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.219551 -1.472199 sample estimates: mean of x mean of y 80.11322 83.95910
T-критерий независимых выборок возвращает значение p 0,0009 , а t-критерий Уэлча возвращает значение p 0,0029 .
Поскольку значение p каждого теста меньше 0,05, мы бы отклонили нулевую гипотезу в каждом тесте и пришли к выводу, что существует статистически значимая разница в средних баллах экзамена между двумя программами.
Несмотря на то, что размеры выборок неравны, t-критерий независимых выборок и t-критерий Уэлча дают одинаковые результаты, поскольку две выборки имели равные дисперсии.
Пример 2: Неравные размеры выборки и неравные дисперсии
Предположим, мы администрируем две программы, призванные помочь студентам лучше сдать определенные экзамены.
Результаты приведены ниже:
Программа 1:
- n (размер выборки): 500
- х (среднее выборочное): 80
- s (выборочное стандартное отклонение): 25
Программа 2:
- n (размер выборки): 20
- х (среднее выборочное): 85
- s (выборочное стандартное отклонение): 5
Следующий код показывает, как создать коробчатую диаграмму в R для визуализации распределения баллов экзамена для каждой программы:
#make this example reproducible set. seeds (1) #create vectors to hold exam scores program1 <- rnorm(500, mean=80, sd=25) program2 <- rnorm(20, mean=85, sd=5) #create boxplots to visualize distribution of exam scores boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))
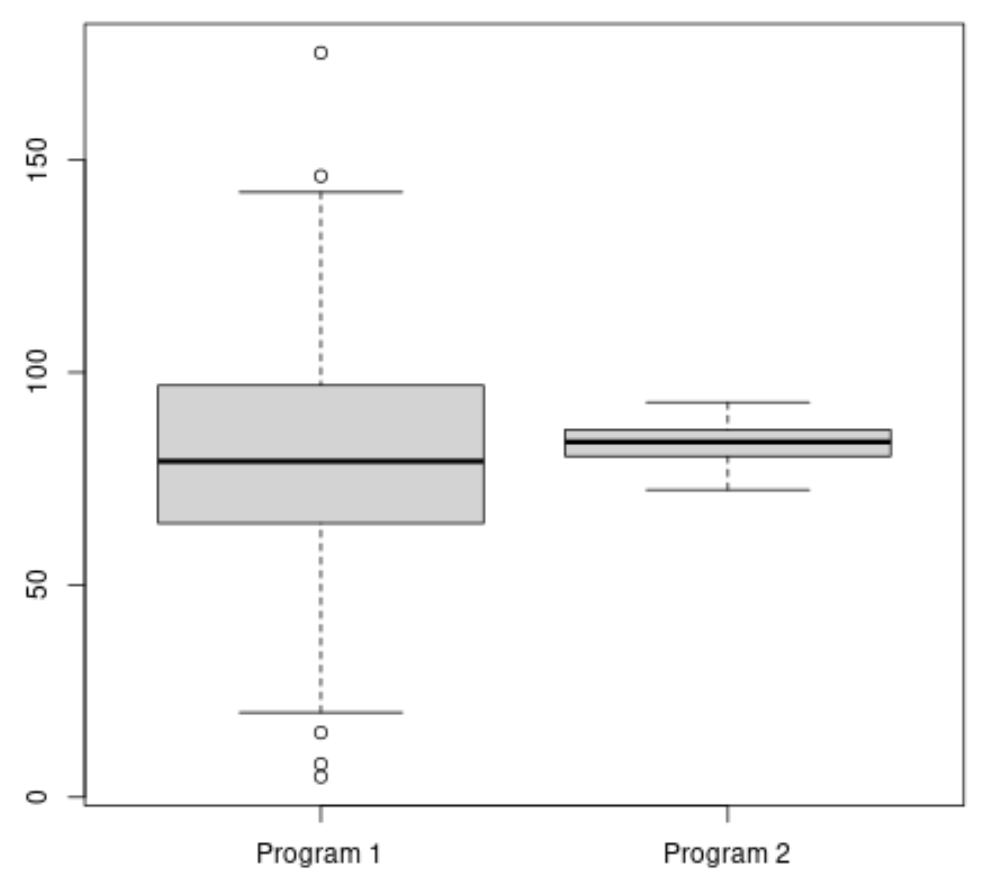
Средний балл экзамена по программе 2 кажется выше, но разница в баллах экзамена по программе 1 намного выше, чем по программе 2.
Следующий код показывает, как выполнить t-критерий независимых выборок с помощью t-критерия Уэлча:
#perform independent samples t-test t. test (program1, program2, var. equal = TRUE ) Two Sample t-test data: program1 and program2 t = -0.5988, df = 518, p-value = 0.5496 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -14.52474 7.73875 sample estimates: mean of x mean of y 80.5661 83.9591 #perform Welch's two sample t-test t. test (program1, program2, var. equal = FALSE ) Welch Two Sample t-test data: program1 and program2 t = -2.1338, df = 74.934, p-value = 0.03613 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.560690 -0.225296 sample estimates: mean of x mean of y 80.5661 83.9591
T-критерий независимых выборок возвращает значение p 0,5496 , а t-критерий Уэлча возвращает значение p 0,0361 .
t-критерий независимых выборок не способен обнаружить разницу в средних баллах на экзамене, но t-критерий Уэлча способен обнаружить статистически значимую разницу.
Поскольку две выборки имели неравные дисперсии, только t-критерий Уэлча смог обнаружить статистически значимую разницу в средних баллах на экзамене, поскольку этот тест не предполагает равные дисперсии между выборками .
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о t-тестах:
Введение в одновыборочный t-критерий
Введение в двухвыборочный t-критерий
Знакомство с t-критерием парных выборок