Как выполнить квадратичную регрессию на калькуляторе ti-84
Когда две переменные имеют линейную связь, мы часто можем использовать простую линейную регрессию для количественной оценки их связи.

Однако, когда две переменные имеют квадратичную связь, мы можем использовать квадратичную регрессию для количественной оценки их связи.

В этом руководстве объясняется, как выполнить квадратичную регрессию на калькуляторе TI-84.
Пример: квадратичная регрессия на калькуляторе TI-84.
Предположим, мы хотим понять взаимосвязь между количеством отработанных часов и счастьем. У нас есть следующие данные о количестве отработанных часов в неделю и уровне счастья (по шкале от 0 до 100) для 11 разных людей:

Выполните следующие шаги, чтобы выполнить квадратичную регрессию на калькуляторе TI-84.
Шаг 1: Визуализируйте данные.
Прежде чем мы сможем использовать квадратичную регрессию, мы должны убедиться, что связь между объясняющей переменной (часы) и переменной ответа (счастье) действительно квадратичная.
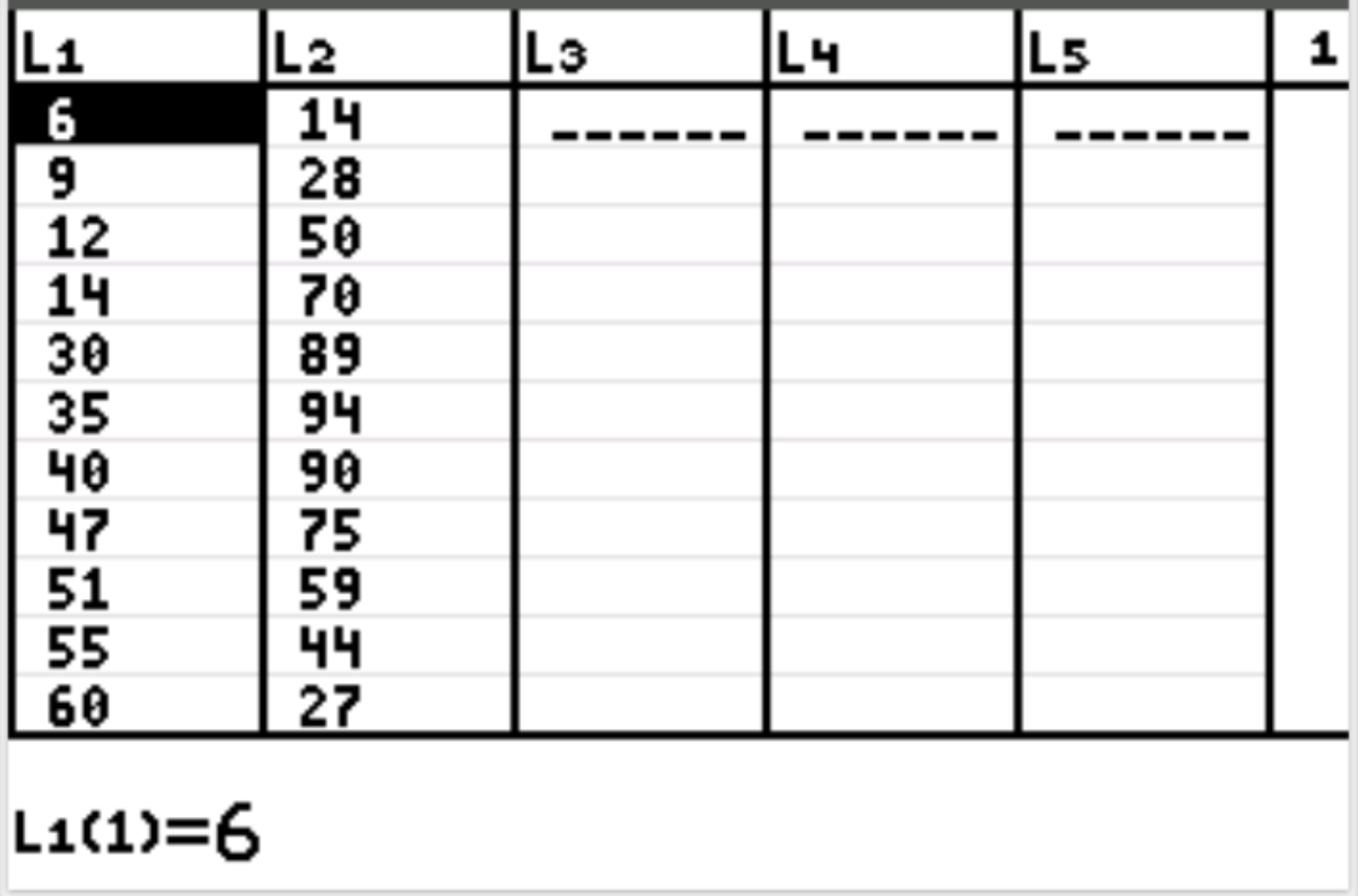
Сначала мы введем значения данных для объясняющей переменной и переменной ответа. Нажмите Stat , затем нажмите EDIT . Введите следующие значения объясняющей переменной (отработанные часы) в столбце L1 и значения переменной ответа (счастье) в столбце L2:
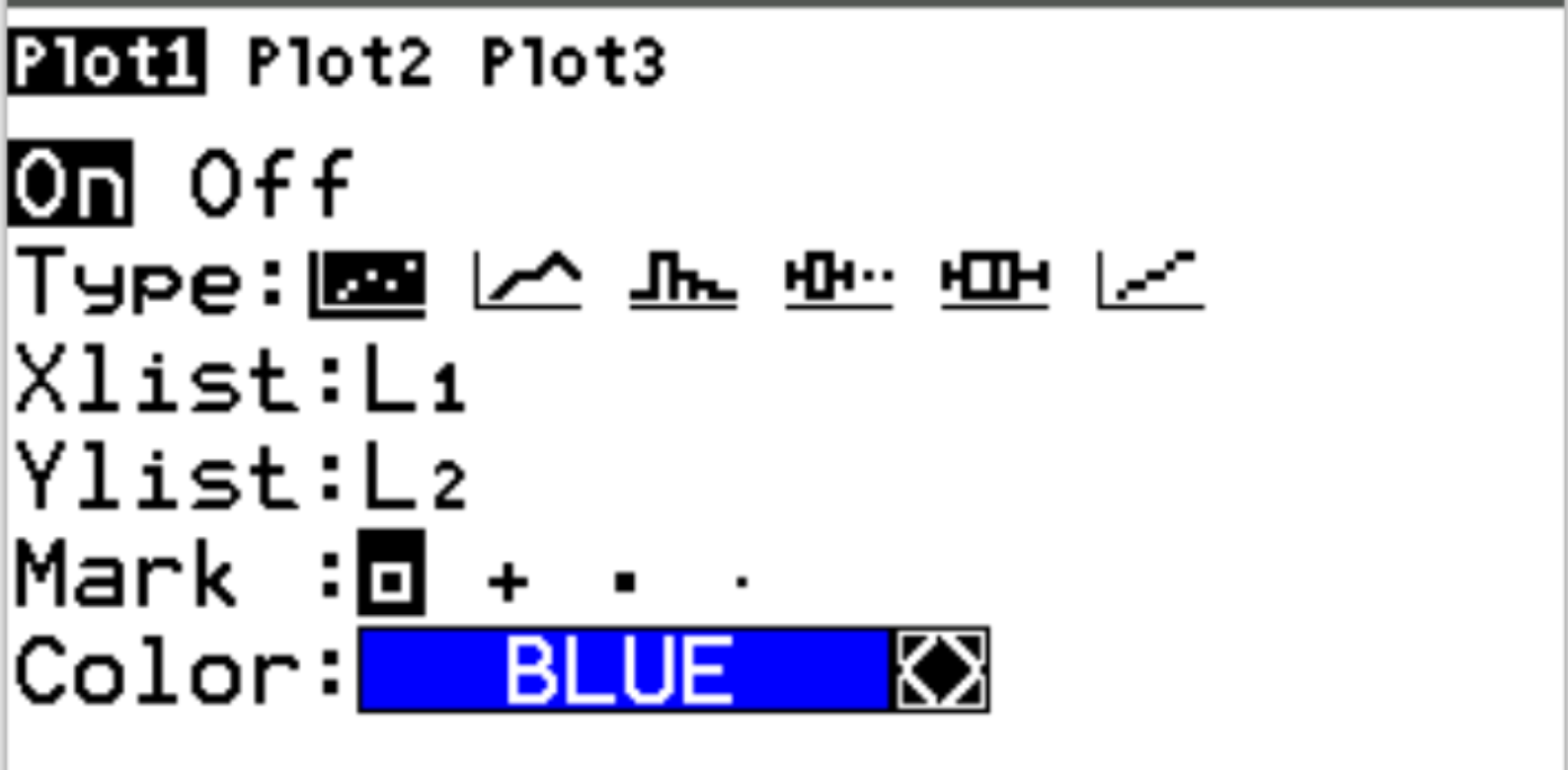
Затем нажмите 2nd , затем нажмите y= , чтобы получить доступ к меню графика статистики . Выделите Plot1 и нажмите Enter . Убедитесь, что построение графика включено и для Xlist и Ylist выбраны L1 и L2 соответственно:
Затем нажмите масштабирование , а затем нажмите 9:ZoomStat . Это автоматически создаст следующее облако точек:

Мы видим, что счастье имеет тенденцию увеличиваться по мере увеличения количества отработанных часов от нуля до определенной точки, но затем начинает уменьшаться по мере дальнейшего увеличения количества отработанных часов.
Эта перевернутая буква «U» на диаграмме рассеяния указывает на то, что существует квадратичная зависимость между отработанными часами и счастьем, а это означает, что нам следует использовать квадратичную регрессию для количественной оценки этой зависимости.
Шаг 2: Выполните квадратичную регрессию.
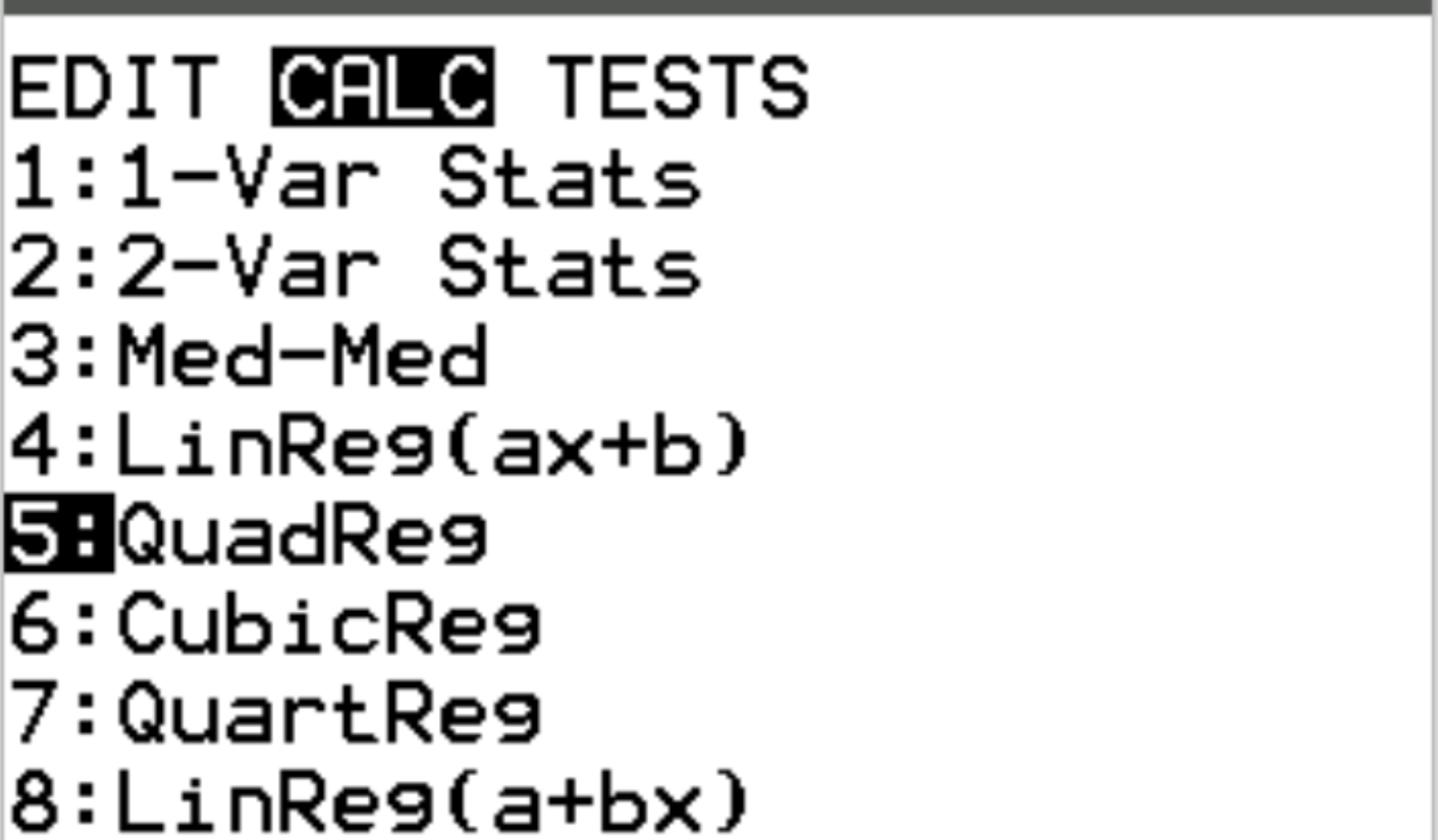
Далее мы выполним квадратичную регрессию. Нажмите Stat , затем перейдите к CALC . Затем прокрутите до 5:QuadReg и нажмите Enter .
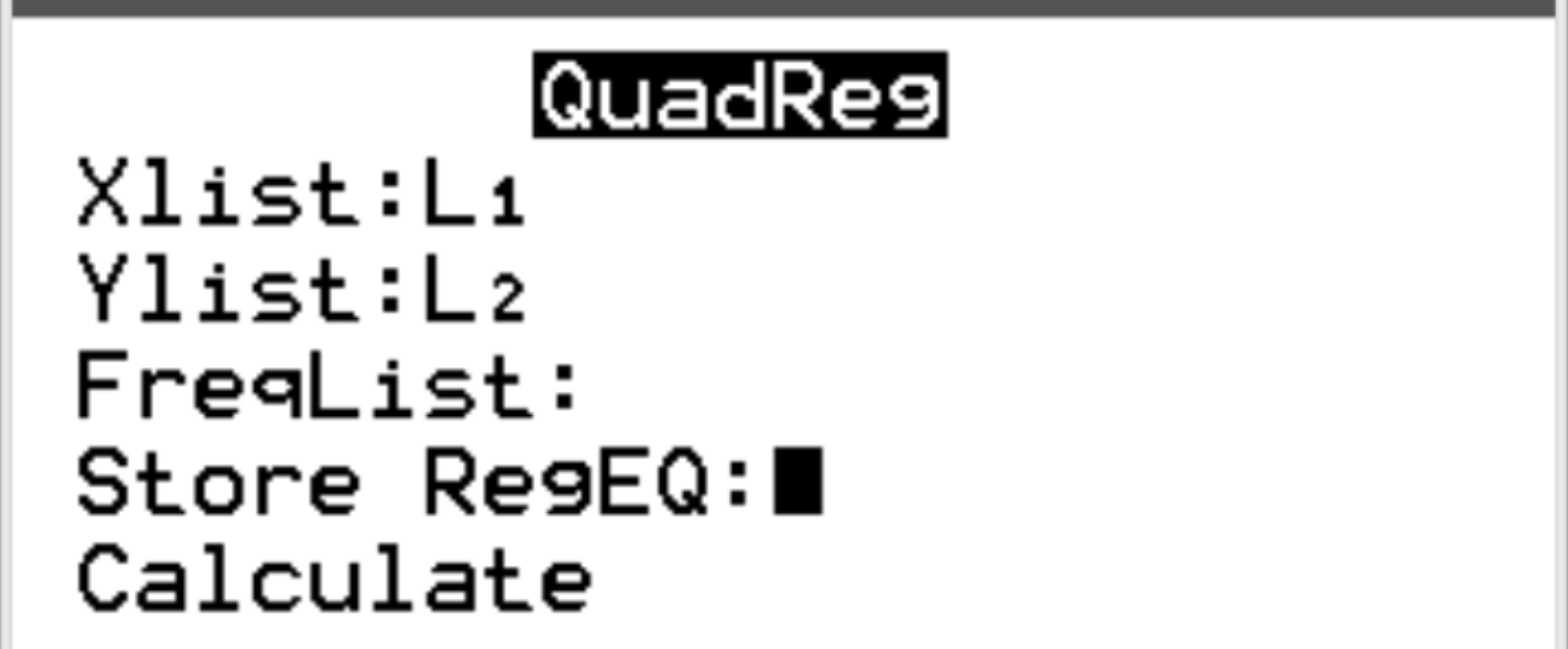
Для Xlist и Ylist убедитесь, что выбраны L1 и L2, поскольку это столбцы, которые мы использовали для ввода наших данных. Оставьте FreqList пустым. Прокрутите вниз до пункта «Рассчитать» и нажмите Enter .
Автоматически появится следующий вывод:
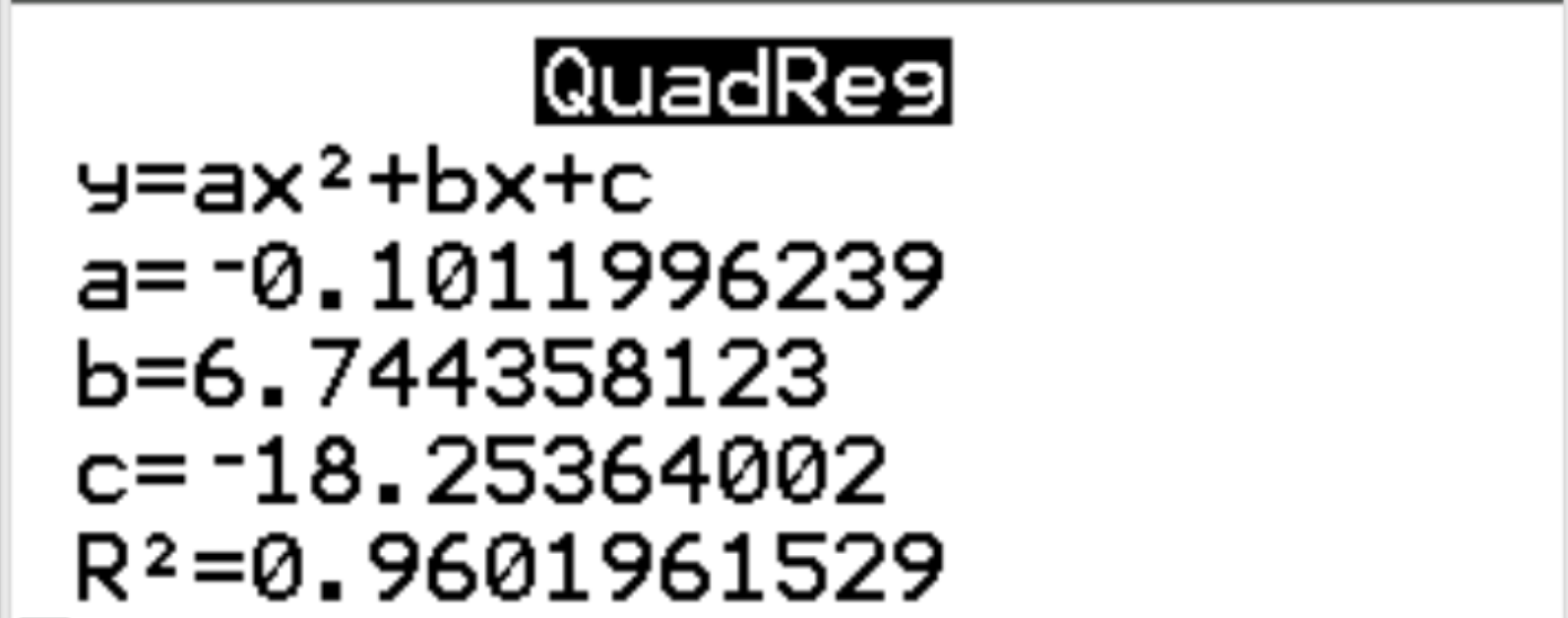
Шаг 3: Интерпретируйте результат.
Из результатов мы видим, что предполагаемое уравнение регрессии имеет вид:
счастье = -0,1012 (часы) 2 + 6,7444 (часы) – 18,2536
Мы можем использовать это уравнение, чтобы найти прогнозируемое счастье человека, учитывая количество часов, которые он работает в неделю.
Например, человек, который работает 60 часов в неделю, будет иметь уровень счастья 22,09 :
счастье = -0,1012(60) 2 + 6,7444(60) – 18,2536 = 22,09
И наоборот, человек, который работает 30 часов в неделю, должен иметь уровень счастья 92,99 :
счастье = -0,1012(30) 2 + 6,7444(30) – 18,2536 = 92,99
Мы также видим, что квадрат r для регрессионной модели равен r 2 = 0,9602 . Это доля дисперсии переменной отклика, которую можно объяснить объясняющими переменными. В этом примере 96,02% изменений счастья можно объяснить часами и временем 2 .