Как рассчитать z-показатели в spss
Z-показатель говорит нам, на сколько стандартных отклонений данное значение отличается от среднего.
Z-показатель данного значения рассчитывается следующим образом:
z-показатель = (x – µ) / σ
Золото:
- х: индивидуальное значение
- μ: средний показатель по численности населения
- σ: стандартное отклонение совокупности
В этом руководстве объясняется, как рассчитать z-показатели в SPSS.
Связанный: Как интерпретировать Z-оценки
Как рассчитать Z-показатели в SPSS
Предположим, у нас есть следующий набор данных, показывающий годовой доход (в тысячах) 15 человек:
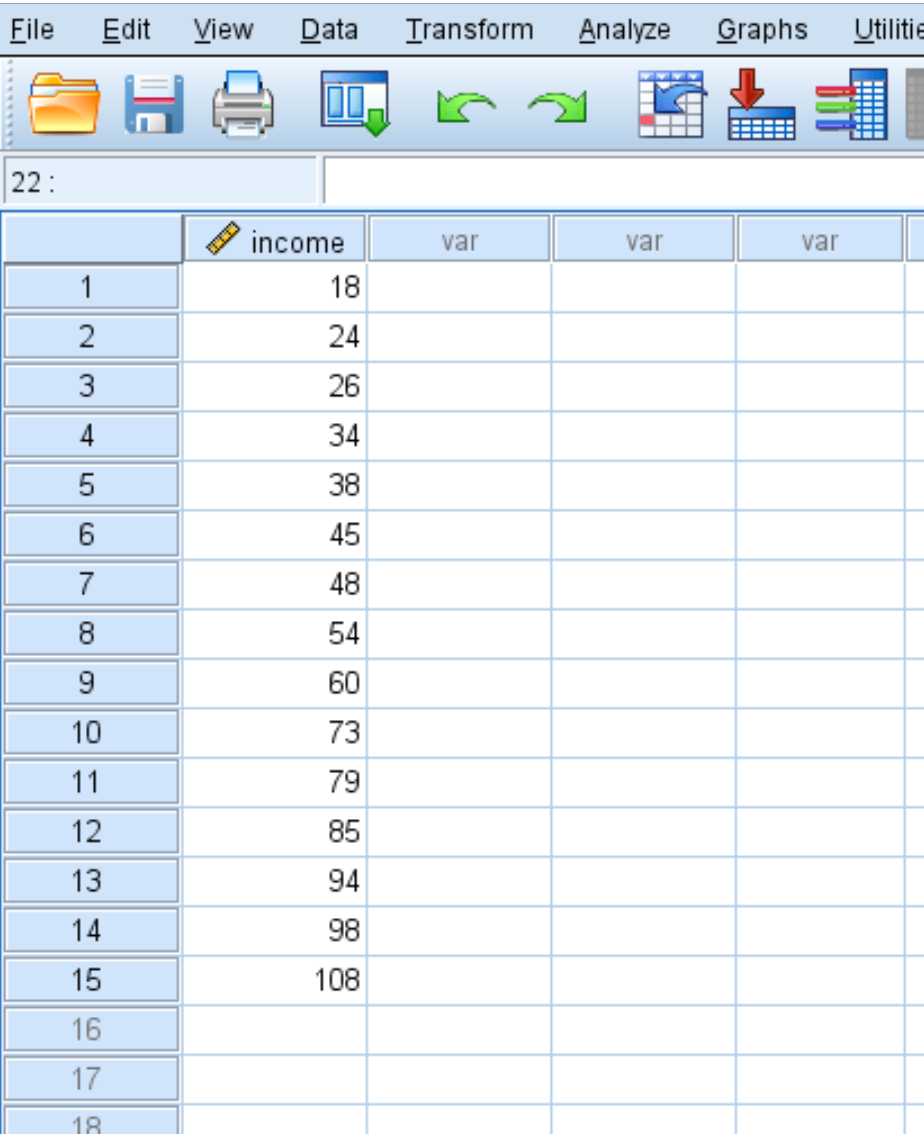
Чтобы вычислить z-показатели для каждого значения в наборе данных, щелкните вкладку «Анализ» , затем «Описательная статистика» , затем «Описательные данные» :
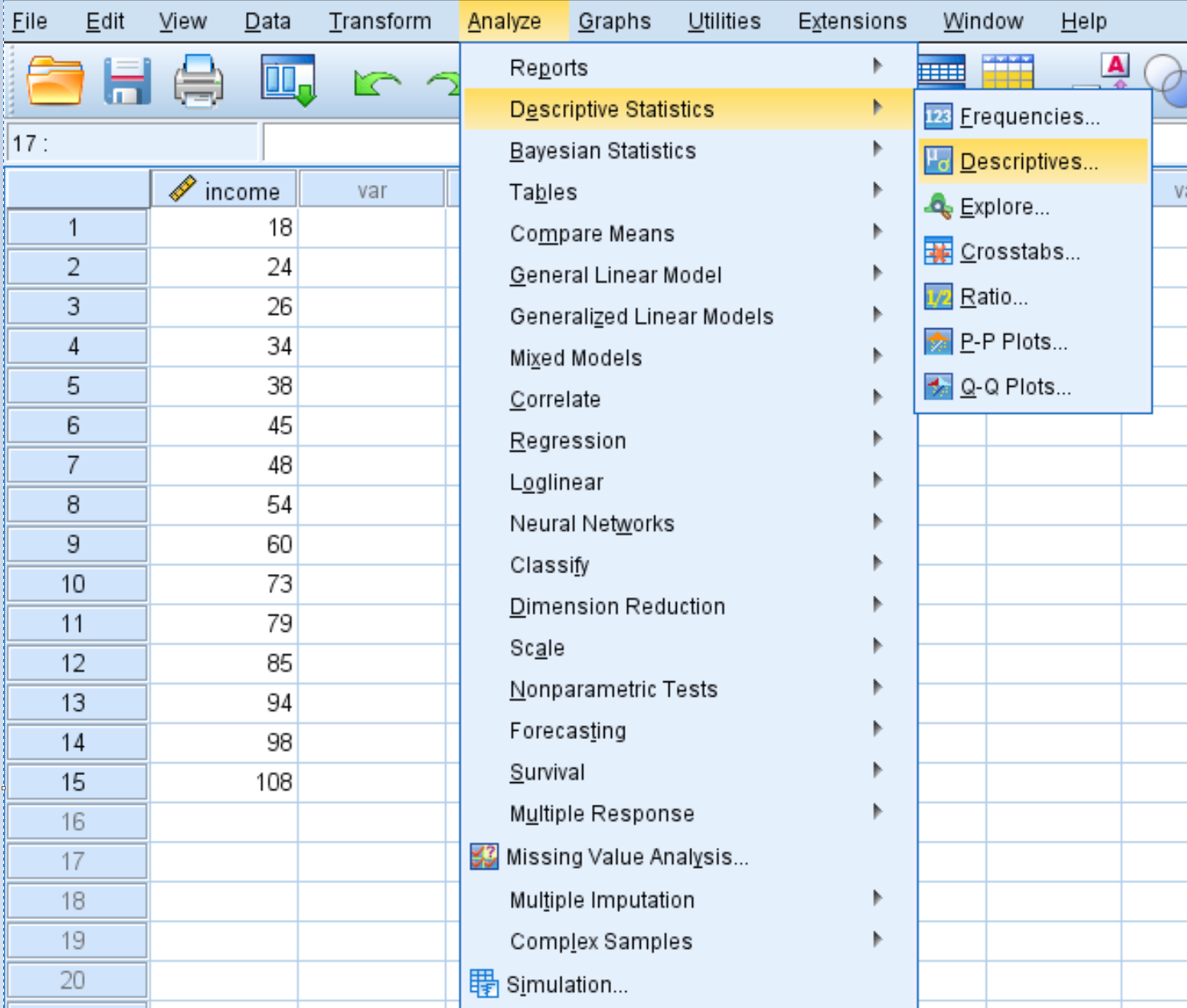
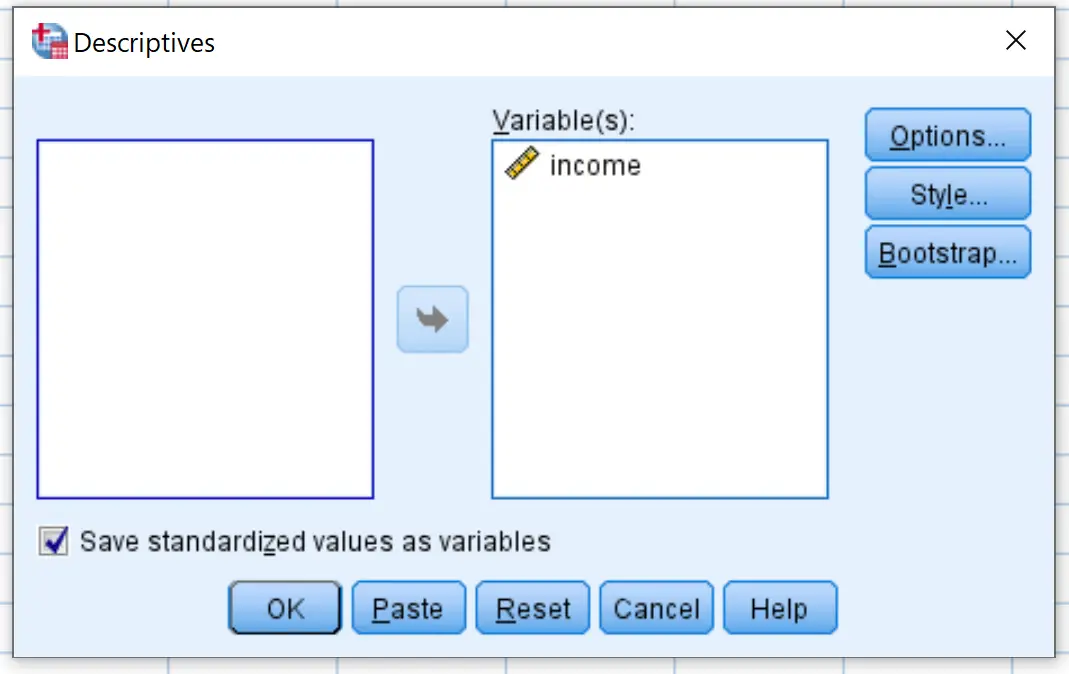
В появившемся новом окне перетащите переменную дохода в поле с надписью «Переменные».
Убедитесь, что установлен флажок рядом с пунктом «Сохранить стандартизированные значения как переменные» , а затем нажмите «ОК» .
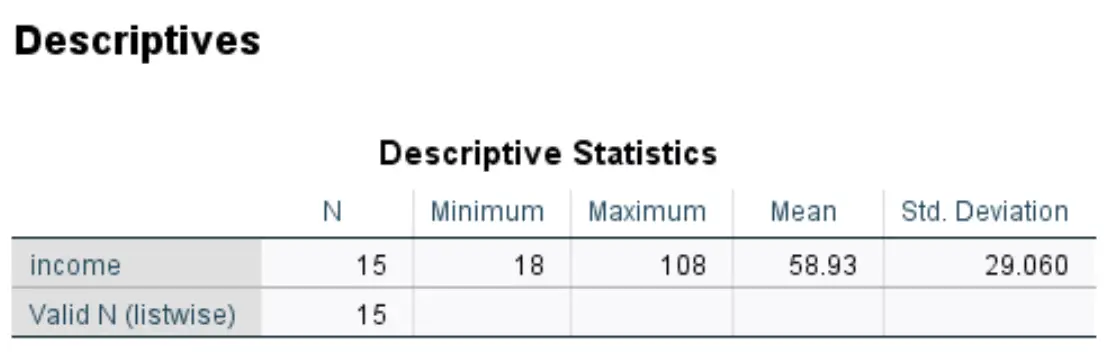
Как только вы нажмете «ОК» , SPSS создаст таблицу описательной статистики для вашего набора данных:
SPSS также создаст новый столбец значений, в котором будет отображаться z-показатель для каждого исходного значения в вашем наборе данных:
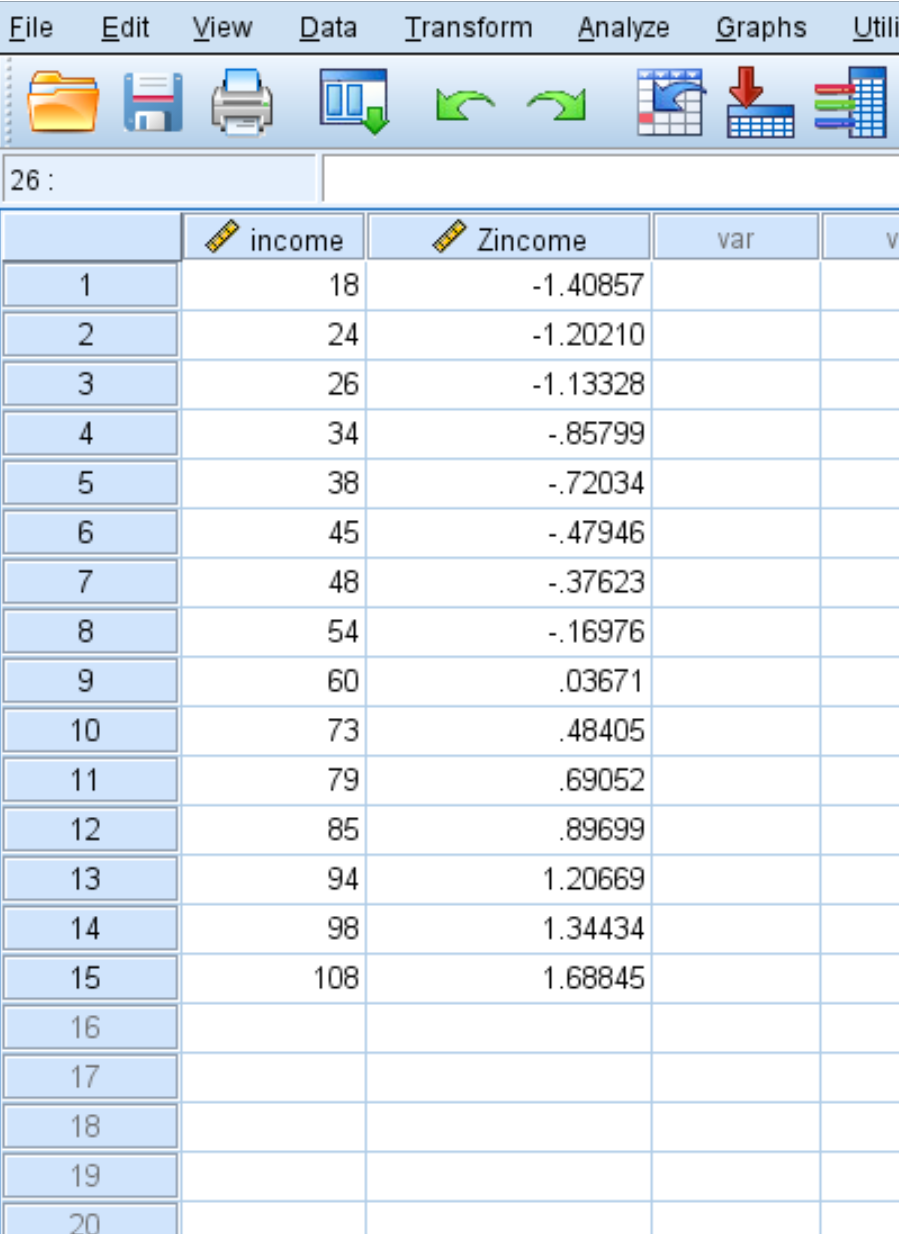
Каждый из z-показателей рассчитывается по формуле z = (x – µ)/σ
Например, z-показатель для значения дохода 18 равен:
z = (18 – 58,93)/29,060 = -1,40857 .
Z-показатели для всех остальных значений данных рассчитываются таким же образом.
Как интерпретировать Z-показатели
Помните, что z-показатель просто говорит нам, на сколько стандартных отклонений значение отличается от среднего.
Показатель z может быть положительным, отрицательным или равным нулю:
- Положительный показатель z указывает на то, что конкретное значение выше среднего.
- Отрицательный показатель z указывает на то, что конкретное значение ниже среднего.
- Нулевой z-показатель указывает на то, что конкретное значение равно среднему.
В нашем примере мы обнаружили, что среднее значение равно 58,93, а стандартное отклонение — 29,060.
Итак, первое значение в нашем наборе данных было 18, которое имело z-показатель (18 – 58,93) / 29,060 = -1,40857 .
Это означает, что значение «18» на 1,40857 стандартных отклонений ниже среднего.
И наоборот, последнее значение в наших данных было 108, что соответствовало z-показателю (108 – 58,93) / 29,060 = 1,68845 .
Это означает, что значение «108» на 1,68845 стандартных отклонений выше среднего.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SPSS:
Как рассчитать описательную статистику для переменных в SPSS
Как рассчитать пятизначную сводку в SPSS
Как идентифицировать выбросы в SPSS