Абсолютная частота

В этой статье объясняется значение абсолютной частоты в статистике. Таким образом, вы узнаете, как получить абсолютную частоту набора данных, два решенных упражнения и, кроме того, различия с другими типами статистических частот.

Какова абсолютная частота?

В статистике абсолютная частота — это количество раз, когда значение появляется в наборе данных. Проще говоря, абсолютная частота — это количество повторений результата.

Например, если семь человек в опросе ответили, что их любимый цвет — красный, то абсолютная частота красного цвета равна 7.

Следовательно, сумма абсолютных частот всех значений равна общему количеству данных в статистической выборке.

Обычно буква f с индексом i используется для обозначения абсолютной частоты значения i , поэтому символ абсолютной частоты — _fi .

Как рассчитать абсолютную частоту

Чтобы получить абсолютные частоты набора данных, необходимо выполнить следующие шаги:

1. Если переменная дискретная, создайте массив всех различных значений, которые встречаются в наборе данных, то есть поместите каждое отдельное значение в строку таблицы.
2. Если переменная непрерывная, сгруппируйте данные по интервалам и создайте таблицу со всеми интервалами.
3. Подсчитайте, сколько раз значение появляется в наборе данных, и запишите результат в таблицу частот.
4. Повторите предыдущий шаг для каждого значения в выборке данных.

Примеры абсолютной частоты

После того, как мы ознакомились с определением абсолютной частоты и теорией ее расчета, мы рассмотрим два примера, чтобы вы поняли, как это делается. В первом примере мы определим абсолютные частоты дискретной переменной, а во втором примере — непрерывной переменной, поскольку процедура незначительно варьируется в зависимости от случая.

Пример 1: дискретная переменная

• Оценки, полученные по статистике в классе из 30 учеников, следующие. Какова абсолютная частота каждой ноты?

В данном случае это дискретная переменная, поскольку могут быть только целые числа, поэтому нет необходимости группировать их по интервалам.

Поэтому просто посчитайте количество раз, когда появляется каждое значение, и запишите его в таблицу частот:

Обратите внимание, что сумма всех абсолютных частот равна общему количеству точек данных. Если это правило не соблюдено, значит, вы забыли посчитать какие-то данные.

Пример 2: непрерывная переменная

• Был измерен рост 20 человек и получены результаты, указанные ниже. Разделите данные на интервалы и найдите абсолютную частоту каждого интервала.

Данные в этом образце имеют непрерывное распределение, поскольку числа могут быть десятичными. Поэтому нам необходимо сгруппировать данные по интервалам, в данном случае мы сделаем интервалы шириной в 10 десятых.

Итак, подсчитываем количество данных в каждом интервале и представляем абсолютные частоты в таблице:

Абсолютная частота и совокупная абсолютная частота

Как следует из названия, совокупная абсолютная частота — это еще один тип частоты, используемый в статистике и связанный с абсолютной частотой.

Совокупная абсолютная частота значения равна сумме абсолютной частоты самого значения плюс абсолютные частоты всех предыдущих значений.

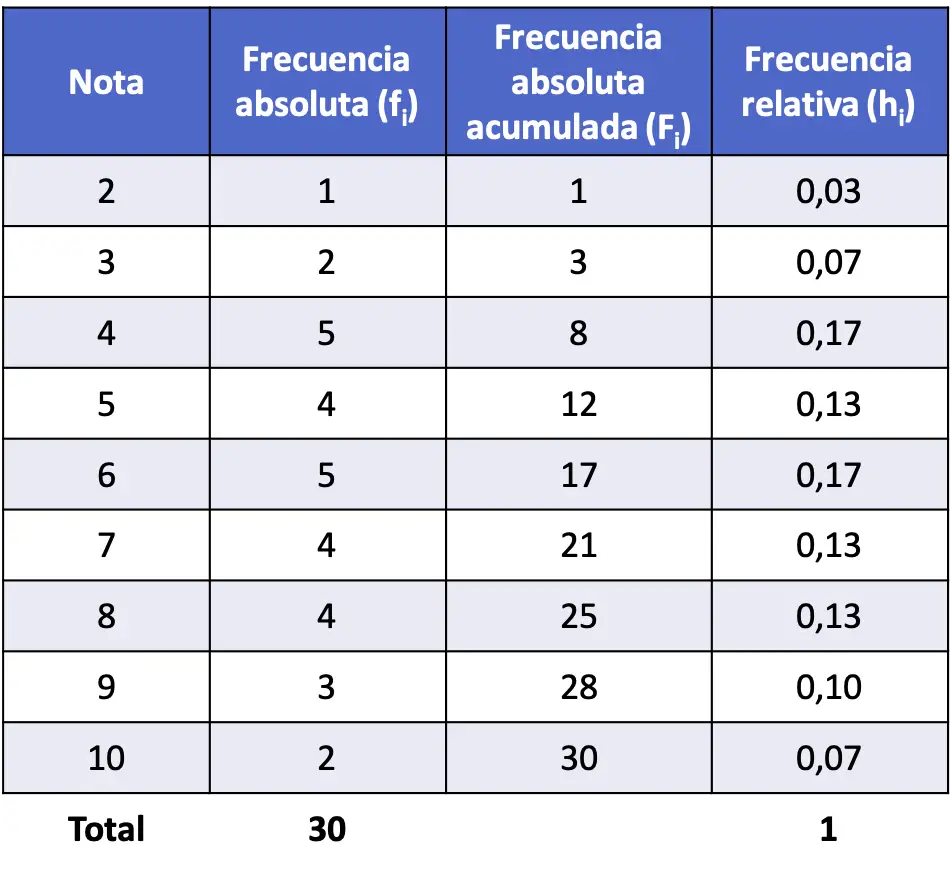
В качестве примера ниже вы можете увидеть расчет накопленных абсолютных частот первого упражнения, решенного выше:

Абсолютная частота и относительная частота

В статистике относительная частота — это тип частоты, отличный от двух, рассмотренных выше, поскольку он представляет собой процент каждого значения по сравнению с общим количеством. Вот почему в этом разделе мы увидим разницу между этими двумя понятиями.

Разница между абсолютной частотой и относительной частотой заключается в том, что абсолютная частота — это абсолютное количество значений в выборке, а относительная частота — это доля каждого значения в общем количестве.

Следовательно, относительная частота рассчитывается путем деления абсолютной частоты на общее количество данных.