Анализ главных компонентов в r: пошаговый пример

Анализ главных компонентов, часто сокращенно PCA, представляет собой метод машинного обучения без учителя , целью которого является поиск главных компонентов – линейных комбинаций исходных предикторов – которые объясняют большую часть изменений в наборе данных.

Цель PCA — объяснить большую часть изменчивости в наборе данных с меньшим количеством переменных, чем в исходном наборе данных.

Для данного набора данных с p переменными мы могли бы изучить диаграммы рассеяния каждой парной комбинации переменных, но количество диаграмм рассеяния может очень быстро стать большим.

Для p- предикторов существует p(p-1)/2 облаков точек.

Итак, для набора данных с p = 15 предикторами будет 105 различных диаграмм рассеяния!

К счастью, PCA предлагает способ найти низкоразмерное представление набора данных, которое отражает как можно большую часть вариаций данных.

Если мы сможем отразить большую часть изменений всего в двух измерениях, мы сможем спроецировать все наблюдения из исходного набора данных на простую диаграмму рассеяния.

Способ нахождения основных компонентов следующий:

_{Учитывая набор данных с} p _{предикторами} : _

• _{Z м = ΣΦ jm _}
• Z ₁ — это линейная комбинация предикторов, которая фиксирует как можно большую дисперсию.
• Z ₂ является следующей линейной комбинацией предикторов, которая фиксирует наибольшую дисперсию, будучи при этом ортогональной (т. е. некоррелированной) с Z ₁ .
• Z ₃ тогда является следующей линейной комбинацией предикторов, которая фиксирует наибольшую дисперсию, будучи ортогональной Z ₂ .
• И так далее.

На практике мы используем следующие шаги для расчета линейных комбинаций исходных предикторов:

1. Масштабируйте каждую переменную так, чтобы ее среднее значение было равно 0, а стандартное отклонение равно 1.

2. Рассчитайте ковариационную матрицу для масштабируемых переменных.

3. Вычислить собственные значения ковариационной матрицы.

Используя линейную алгебру, мы можем показать, что собственный вектор, соответствующий наибольшему собственному значению, является первым главным компонентом. Другими словами, именно эта комбинация предикторов объясняет наибольшую дисперсию данных.

Собственный вектор, соответствующий второму по величине собственному значению, является вторым главным компонентом и так далее.

В этом руководстве представлен пошаговый пример того, как выполнить этот процесс в R.

Шаг 1. Загрузите данные

Сначала мы загрузим пакет Tidyverse , который содержит несколько полезных функций для визуализации и управления данными:

 library (tidyverse)

Для этого примера мы будем использовать набор данных USArrests , встроенный в R, который содержит количество арестов на 100 000 жителей в каждом штате США в 1973 году за убийства , нападения и изнасилования .

Он также включает процент населения каждого штата, проживающего в городских районах, UrbanPop .

Следующий код показывает, как загрузить и отобразить первые строки набора данных:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Шаг 2: Рассчитайте основные компоненты

После загрузки данных мы можем использовать встроенную функцию R prcomp() для расчета основных компонентов набора данных.

Обязательно укажите масштаб = TRUE , чтобы каждая переменная в наборе данных была масштабирована так, чтобы иметь среднее значение 0 и стандартное отклонение 1 перед расчетом главных компонентов.

Также обратите внимание, что собственные векторы R по умолчанию указывают в отрицательном направлении, поэтому мы умножим их на -1, чтобы поменять знаки.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

Мы видим, что первый главный компонент (PC1) имеет высокие значения для убийств, нападений и изнасилований, что указывает на то, что этот главный компонент описывает наибольшее изменение этих переменных.

Мы также можем видеть, что второй главный компонент (PC2) имеет высокое значение для UrbanPop, что указывает на то, что этот главный компонент уделяет особое внимание городскому населению.

Обратите внимание, что оценки основных компонентов для каждого состояния хранятся в results$x . Мы также умножим эти оценки на -1, чтобы поменять знаки:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Шаг 3. Визуализируйте результаты с помощью биграфика

Затем мы можем создать биграфик — график, который проецирует каждое из наблюдений в наборе данных на диаграмму рассеяния, которая использует первый и второй главные компоненты в качестве осей:

Обратите внимание, что масштаб = 0 гарантирует, что стрелки на графике масштабируются для представления нагрузок.

 biplot(results, scale = 0 )

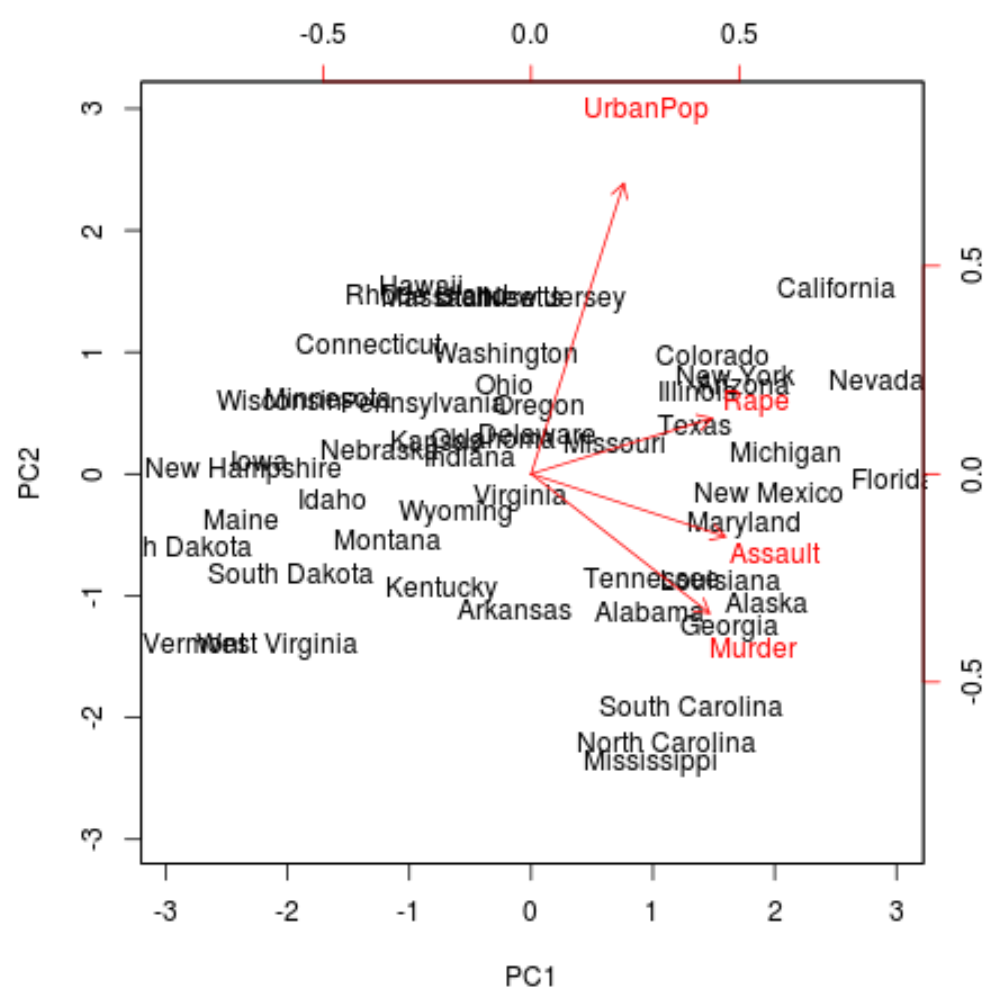
На графике мы можем увидеть каждое из 50 состояний, представленных в простом двумерном пространстве.

Состояния, расположенные близко друг к другу на графике, имеют схожие шаблоны данных относительно переменных в исходном наборе данных.

Мы также можем видеть, что некоторые государства более тесно связаны с определенными преступлениями, чем другие. Например, Джорджия — штат, наиболее близкий к переменной «Убийство» на графике.

Если мы посмотрим на штаты с самым высоким уровнем убийств в исходном наборе данных, мы увидим, что Грузия фактически возглавляет список:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Шаг 4. Найдите дисперсию, объясняемую каждым главным компонентом.

Мы можем использовать следующий код для расчета общей дисперсии исходного набора данных, объясненной каждым основным компонентом:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

По результатам мы можем наблюдать следующее:

• Первый главный компонент объясняет 62% общей дисперсии в наборе данных.
• Второй главный компонент объясняет 24,7% общей дисперсии набора данных.
• Третий главный компонент объясняет 8,9% общей дисперсии набора данных.
• Четвертый главный компонент объясняет 4,3% общей дисперсии набора данных.

Таким образом, первые два главных компонента объясняют большую часть общей дисперсии данных.

Это хороший знак, поскольку предыдущий биграфик проецировал каждое из наблюдений из исходных данных на диаграмму рассеяния, которая учитывала только первые два главных компонента.

Таким образом, имеет смысл изучить закономерности на биграфике, чтобы определить состояния, похожие друг на друга.

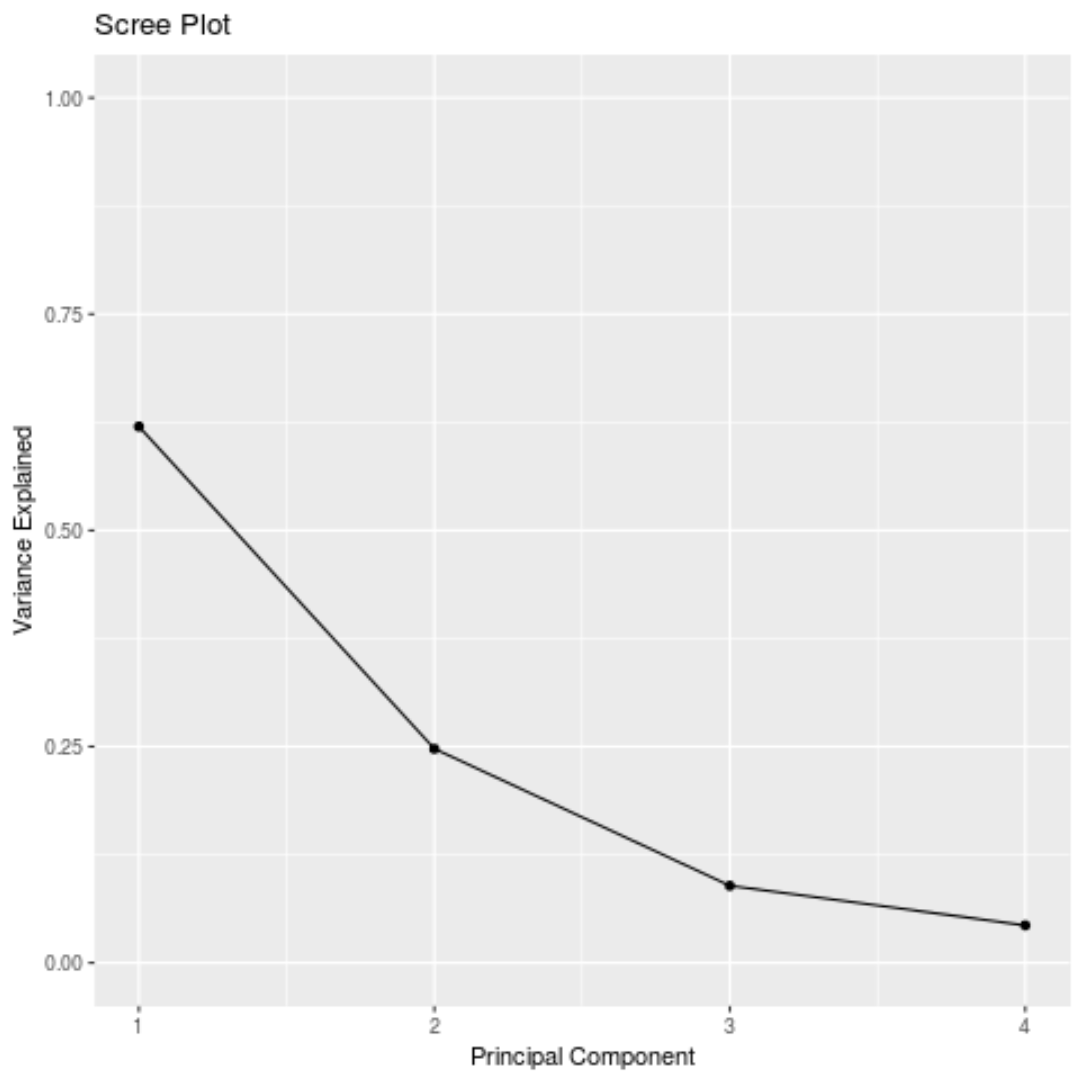
Мы также можем создать график осыпи — график, который отображает общую дисперсию, объясняемую каждым основным компонентом, — для визуализации результатов PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

Анализ главных компонентов на практике

На практике PCA чаще всего используется по двум причинам:

1. Исследовательский анализ данных . Мы используем PCA, когда впервые изучаем набор данных и хотим понять, какие наблюдения в данных наиболее похожи друг на друга.

2. Регрессия главных компонентов . Мы также можем использовать PCA для расчета главных компонентов, которые затем можно использовать в регрессии главных компонентов . Этот тип регрессии часто используется, когда существует мультиколлинеарность между предикторами в наборе данных.

Полный код R, используемый в этом уроке, можно найти здесь .