Введение в ancova (дисперсионный анализ)

ANCOVA означает «ковариационный анализ». Чтобы понять, как работает ANCOVA, необходимо сначала разобраться с ANOVA.

дисперсионный анализ   (дисперсионный анализ) используется для определения того, существует ли статистически значимая разница между средними значениями трех или более независимых групп.

Например, предположим, что мы хотим знать, влияет ли техника обучения на экзаменационные баллы класса студентов. Мы случайным образом разделили класс на три группы. Каждая группа в течение месяца использует разные методики обучения для подготовки к экзамену. В конце месяца все студенты сдают один и тот же экзамен.

Чтобы выяснить, влияет ли техника обучения на результаты экзамена, мы можем выполнить однофакторный дисперсионный анализ, который покажет нам, существует ли статистически значимая разница между средними баллами трех групп.

ANCOVA — это расширение ANOVA, в котором мы хотим определить, существует ли статистически значимая разница между тремя или более независимыми группами после учета одной или несколькихковариат .

Ковариата — это непрерывная переменная, которая изменяется в зависимости от переменной отклика.

Например, предположим, что мы хотим знать, влияет ли техника обучения на экзаменационные баллы, но мы хотим принять во внимание оценку, которую учащийся уже имеет в классе . Мы можем использовать их текущую оценку в качестве ковариаты и выполнить ANCOVA, чтобы определить, существует ли статистически значимая разница между средними баллами экзаменов трех групп.

Это позволяет нам проверить, влияет ли методика обучения на результаты экзамена после устранения влияния ковариаты.

Итак, если мы обнаружим, что существует статистически значимая разница в экзаменационных баллах между тремя методами обучения, мы можем быть уверены, что эта разница существует даже после учета текущей оценки учащихся в классе (т.е. если они у них уже все хорошо или если у них уже все хорошо). не на уроке) .

Предположения АНКОВА

Перед выполнением ANCOVA важно убедиться, что выполняются следующие предположения:

• Ковариата(ы) и факторная переменная(и) независимы . Ковариата и факторная переменная должны быть независимы друг от друга, поскольку добавление ковариатного термина в модель имеет смысл только в том случае, если ковариата и факторная переменная действуют независимо на переменная ответа.
• Ковариата(ы) представляют собой непрерывные данные. Ковариаты должны быть непрерывными (т. е. данные интервала или соотношения).
• Однородность дисперсий . Отклонения между группами должны быть примерно равными.
• Независимость . Наблюдения в каждой группе должны быть независимыми.
• Нормальность . Данные должны быть примерно нормально распределены в каждой группе.
• Никаких экстремальных выбросов . Ни в одной из групп не должно быть экстремальных выбросов, которые могли бы существенно повлиять на результаты ANCOVA.

АНКОВА: пример

Учитель хочет знать, влияют ли три разных метода обучения на результаты экзамена, но он хочет принять во внимание текущую оценку, которую ученик уже имеет в классе.

Он выполнит ANCOVA, используя следующие переменные:

• Факторная переменная: техническое исследование
• Ковариата: текущий счет
• Переменная ответа: оценка экзамена

В следующей таблице представлен набор данных 15 студентов, набранных для участия в исследовании:

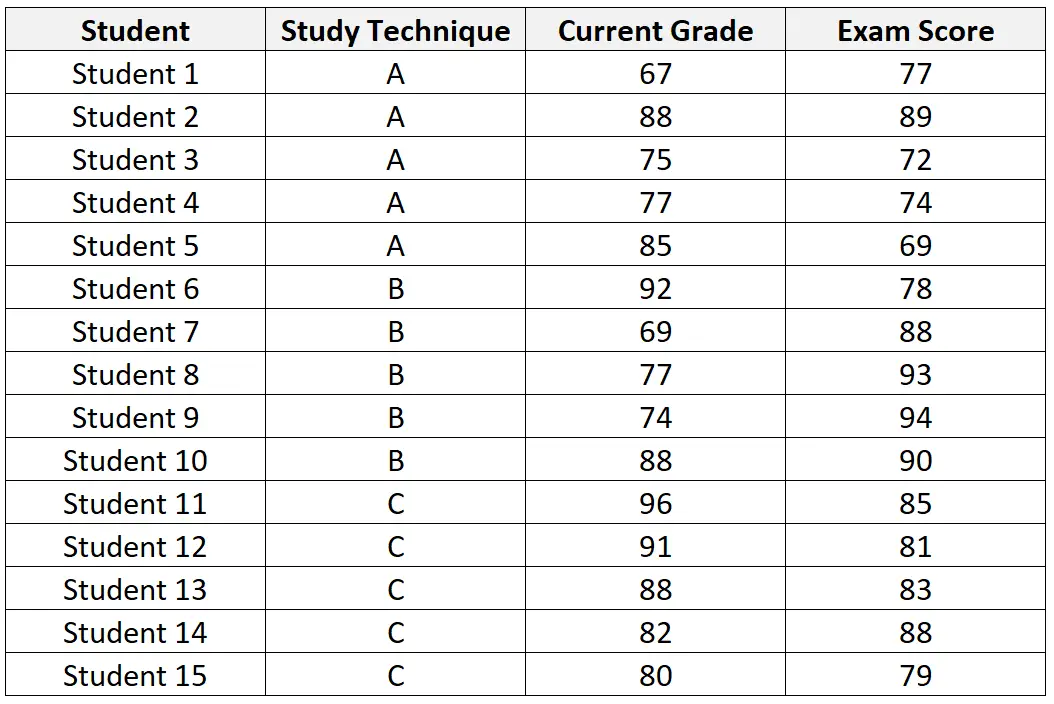
После выполнения ANCOVA для набора данных учитель получает следующие результаты:

Значение p для метода исследования составляет 0,03155 . Поскольку это значение меньше 0,05, мы можем отвергнуть нулевую гипотезу о том, что каждый из методов обучения приводит к одинаковой средней оценке на экзамене, даже после учета текущей оценки ученика в классе .

Чтобы точно определить, какие методы обучения дают разные средние баллы на экзамене, преподавателю необходимо провести апостериорное тестирование .

Дополнительные ресурсы

Как выполнить ANCOVA в Excel
Как выполнить ANCOVA в R
Как выполнить ANCOVA в Python
Различия между ANOVA, ANCOVA, MANOVA и MANCOVA