Как выполнить anova с неравными размерами выборки

Когда речь идет о статистике, студенты часто задают следующий вопрос:

Можно ли выполнить однофакторный дисперсионный анализ, если размеры выборки каждой группы не равны?

Короткий ответ:

Да, вы можете выполнить однофакторный дисперсионный анализ, если размеры выборки не равны. Равные размеры выборки не являются одним из допущений, сделанных в ANOVA.

Однако есть две потенциальные проблемы, которые следует учитывать при выполнении однофакторного дисперсионного анализа с неравными размерами выборки:

(1) Уменьшенная статистическая мощность.

(2) Устойчивость сведена к неравной дисперсии.

В следующих разделах подробно объясняются эти две потенциальные проблемы.

Проблема №1: Снижение статистической мощности

Когда мы используем любой тип статистического теста для сравнения групп, статистическая мощность теста является самой высокой, когда каждая группа имеет одинаковый размер выборки.

Напомним, что статистическая мощность означает вероятность того, что тест обнаружит эффект, когда он действительно существует.

Можно показать, что чем больше различия в размерах выборки между группами, тем ниже статистическая мощность дисперсионного анализа.

Вот почему исследователям обычно нужны равные размеры выборок, чтобы иметь более высокую мощность и, следовательно, большую вероятность обнаружения истинных различий.

Конечно, можно выполнить однофакторный дисперсионный анализ с неравными размерами выборок, но вы должны знать, что мощность однофакторного дисперсионного анализа будет уменьшена.

Проблема № 2: устойчивость снижается до неравной дисперсии

Одно из предположений одностороннего дисперсионного анализа состоит в том, что дисперсия между каждой группой одинакова.

В общем, однофакторный дисперсионный анализ считается устойчивым к нарушениям предположения о равных дисперсиях, но только если каждая группа имеет одинаковый размер выборки .

Итак, если у вас неравные размеры выборок и неравные дисперсии между группами, результатам однофакторного дисперсионного анализа может быть трудно доверять.

Как решить, использовать ли однофакторный дисперсионный анализ с неравными размерами выборки

Если у вас неравные размеры выборок и вы хотите выполнить однофакторный дисперсионный анализ для проверки различий между средними группами, вы можете использовать следующую блок-схему, чтобы решить, как действовать дальше:

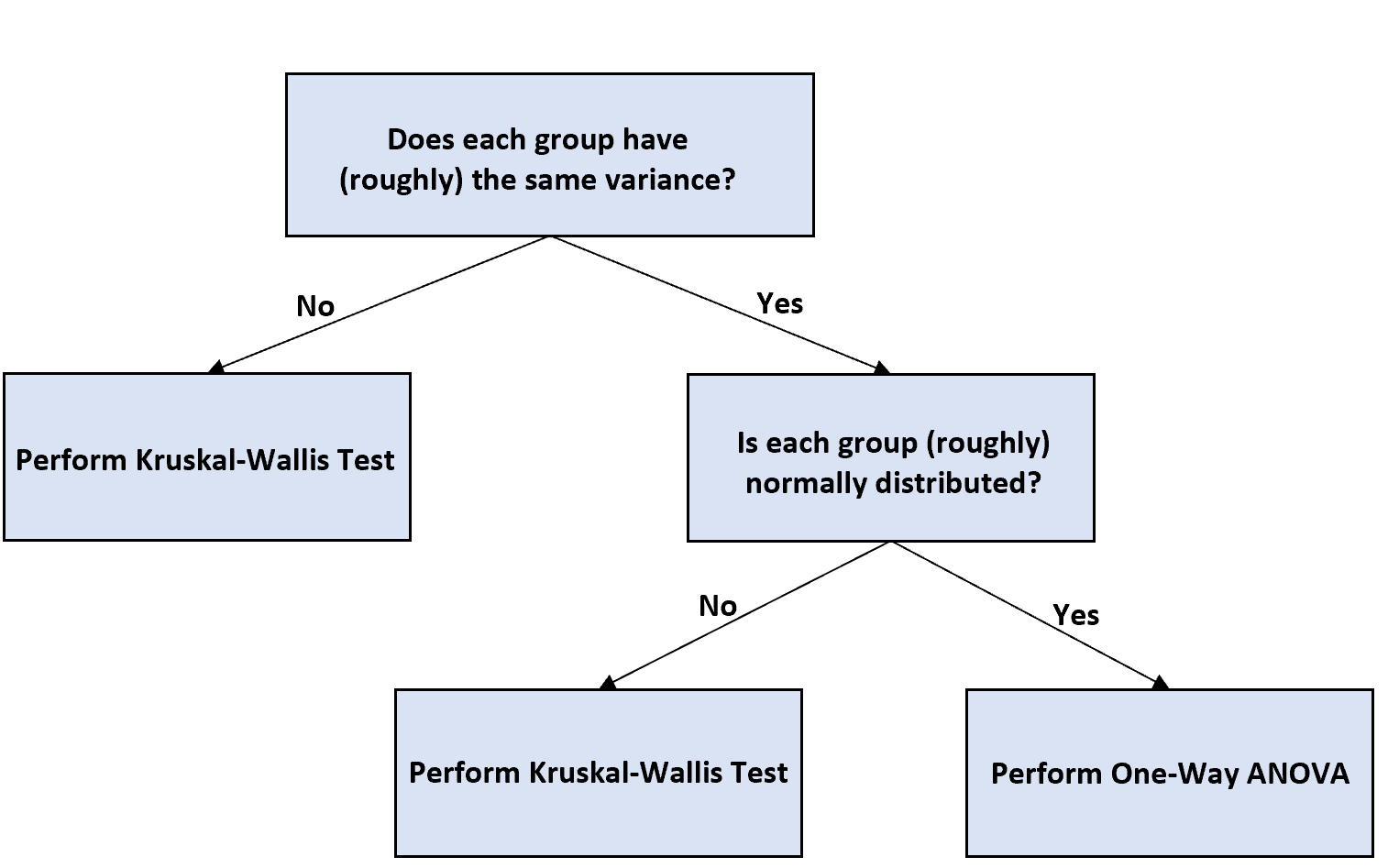
Вот краткое объяснение блок-схемы:

Шаг 1: Определите, имеет ли каждая группа одинаковую дисперсию.

Чтобы определить, имеет ли каждая группа одинаковую дисперсию, вы можете использовать один из двух подходов:

• Создайте коробчатые диаграммы для каждой группы и посмотрите, примерно ли равно распределение значений в каждой группе.
• Выполните формальный статистический тест на равенство дисперсий, например критерий Бартлетта .

Если дисперсии не равны, выполните тест Крускала-Уоллиса , который считается непараметрическим эквивалентом однофакторного дисперсионного анализа.

Если зазоры равны, переходим к следующему шагу.

Шаг 2: Определите, нормально ли распределена каждая группа.

Чтобы определить, распределены ли значения в каждой группе примерно нормально, можно использовать один из двух подходов:

• Создайте гистограммы или графики QQ для каждой группы.
• Выполните формальные статистические тесты, такие как Шапиро-Уилк, Колмогоров-Смиронов, Жарк-Барре или Д’Агостино-Пирсон.

Если каждая группа имеет нормальное распределение, вы можете провести однофакторный дисперсионный анализ и интерпретировать результаты так же, как и любой обычный однофакторный дисперсионный анализ.

Если каждая группа не распределена нормально, вместо этого выполните тест Крускала-Уоллиса.

Дополнительные ресурсы

Введение в однофакторный дисперсионный анализ
Как проверить предположения ANOVA
Введение в тест Крускала-Уоллиса
Как интерпретировать значение F и значение P в ANOVA