Anova против регрессии: в чем разница?
В статистике обычно используются две модели: ANOVA и регрессионные модели.
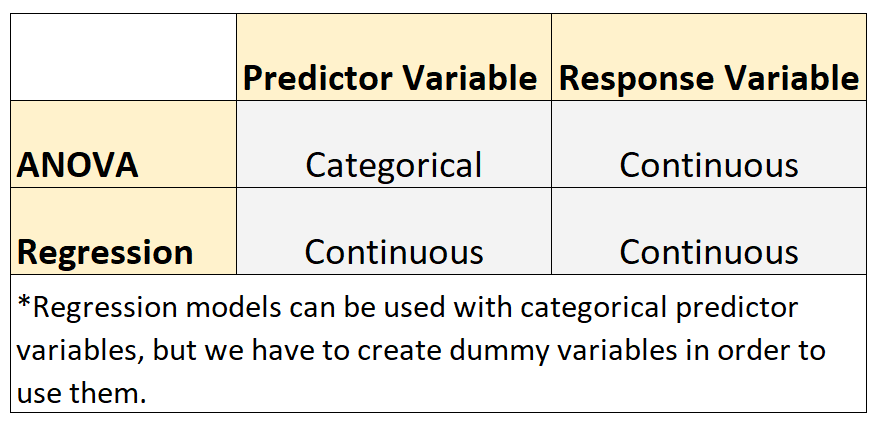
Эти два типа моделей имеют следующее сходство:
- Переменная отклика в каждой модели является непрерывной. Примеры непрерывных переменных включают вес, рост, длину, ширину, время, возраст и т. д.
Однако эти два типа моделей имеют следующее различие :
- Модели ANOVA используются, когда переменные-предикторы являются категориальными. Примеры категориальных переменных включают уровень образования, цвет глаз, семейное положение и т. д.
- Модели регрессии используются, когда переменные-предикторы являются непрерывными.*
*Модели регрессии можно использовать с категориальными переменными-предикторами, но для их использования нам необходимо создать фиктивные переменные .
Следующие примеры показывают, когда на практике следует использовать модели ANOVA или регрессии.
Пример 1: Предпочтительная модель ANOVA
Предположим, биолог хочет понять, приводят ли четыре разных удобрения к одинаковому среднему росту растений (в дюймах) за месячный период. Чтобы проверить это, она применяет каждое удобрение к 20 растениям и записывает рост каждого растения через месяц.
В этом сценарии биолог должен использовать однофакторную модель ANOVA для анализа различий между удобрениями, поскольку существует предикторная переменная, и она является категориальной.
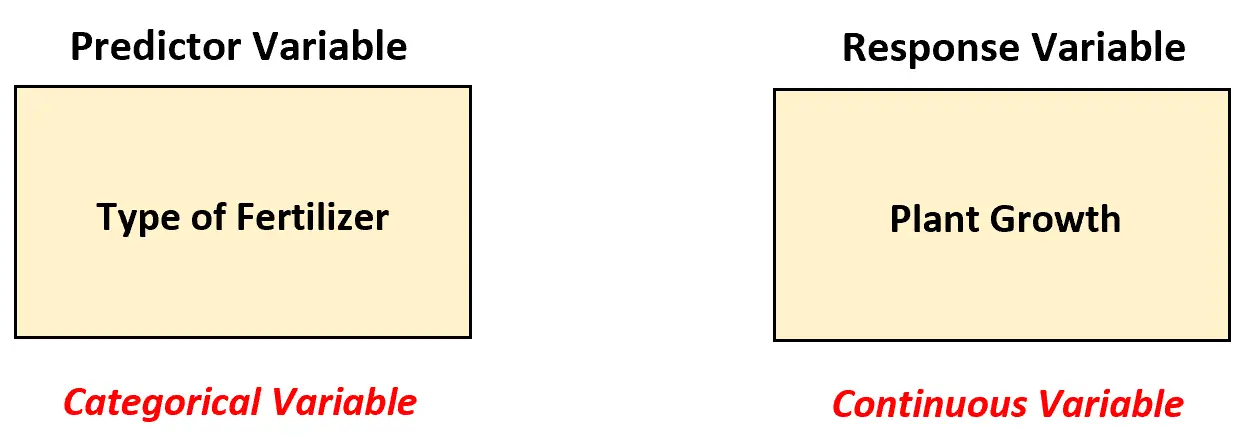
Другими словами, значения переменной-предиктора можно разделить на следующие «категории»:
- Удобрение 1
- Удобрение 2
- Удобрение 3
- Удобрение 4
Односторонний дисперсионный анализ подскажет биологу, одинаков ли средний рост растений при использовании четырех различных удобрений.
Пример 2: Предпочтительная модель регрессии
Допустим, агент по недвижимости хочет понять взаимосвязь между площадью и ценой недвижимости. Чтобы проанализировать эту взаимосвязь, он собирает данные о площади и цене 200 домов в конкретном городе.
В этом сценарии агент по недвижимости должен использовать простую модель линейной регрессии для анализа взаимосвязи между этими двумя переменными, поскольку переменная-предиктор (площадь в квадратных метрах) является непрерывной.
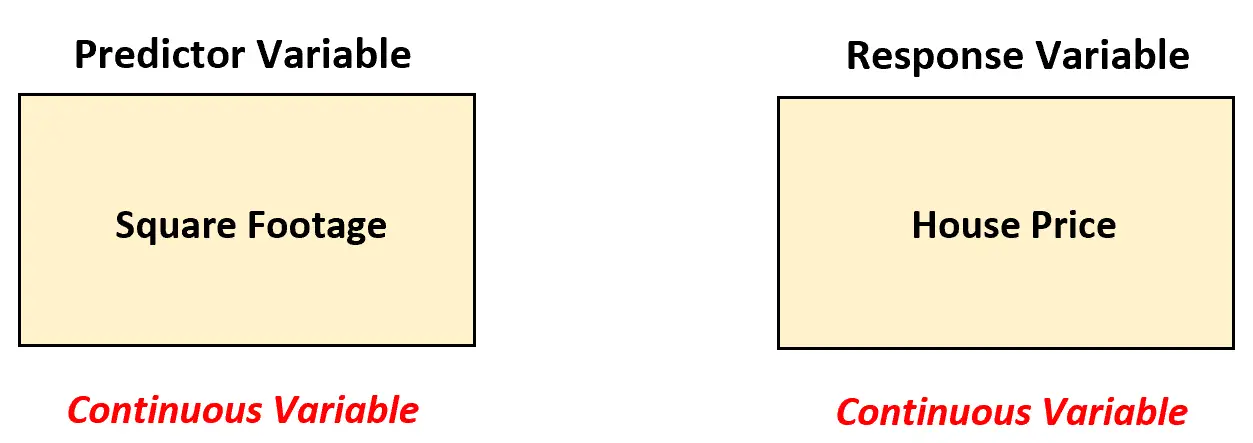
Используя простую линейную регрессию, агент по недвижимости может подобрать следующую модель регрессии:
Цена недвижимости = β 0 + β 1 (площадь квадрата)
Значение β 1 будет представлять собой среднее изменение цены дома, связанное с каждым дополнительным квадратным футом.
Это позволит агенту по недвижимости количественно оценить взаимосвязь между площадью и ценой недвижимости.
Пример 3: Модель регрессии с предпочтительными фиктивными переменными
Предположим, агент по недвижимости хочет понять взаимосвязь между переменными-предикторами «площадь в квадратных метрах» и «тип дома» (одна семья, квартира, таунхаус) с переменной ответа — ценой недвижимости.
В этом сценарии агент по недвижимости может использовать множественную линейную регрессию, преобразуя «тип дома» в фиктивную переменную, поскольку в настоящее время это категориальная переменная.
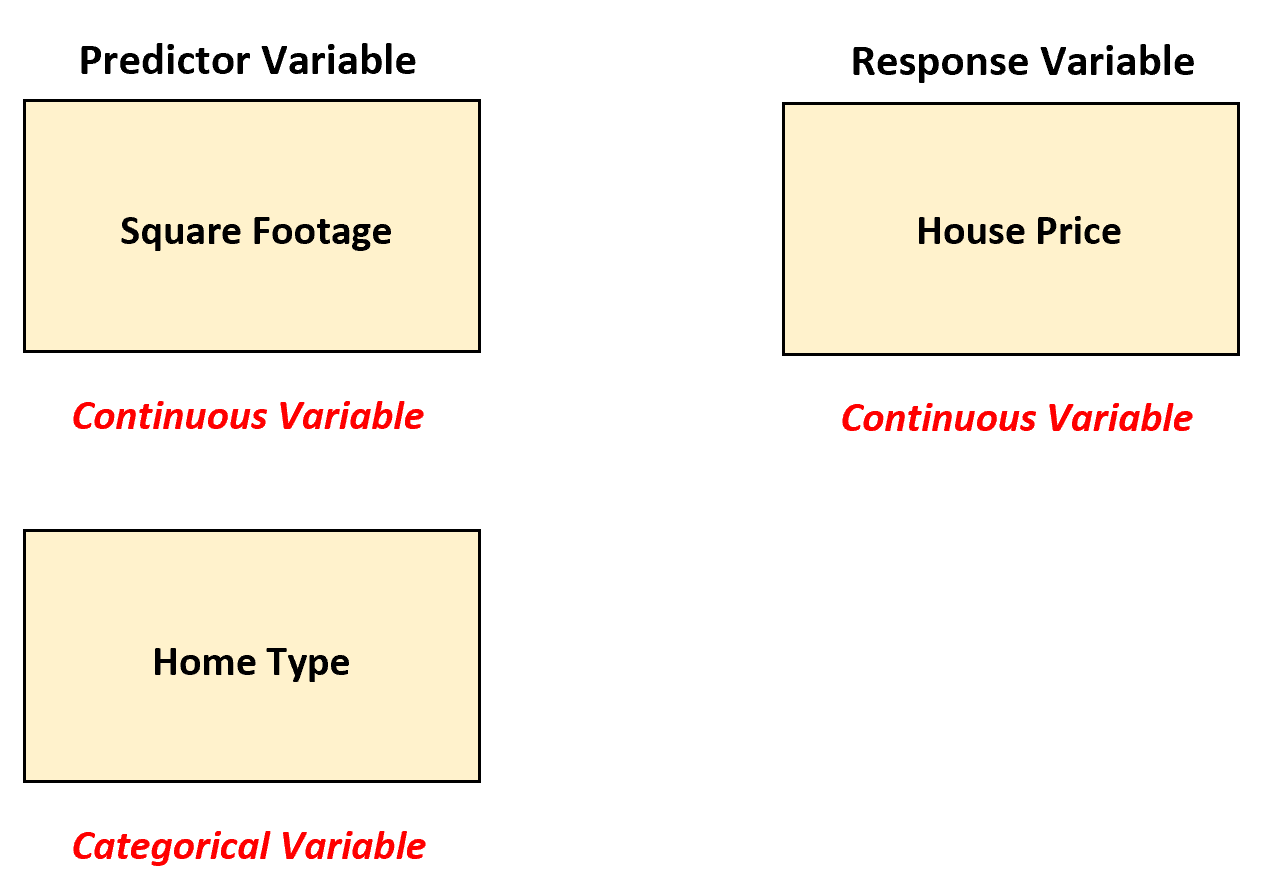
Затем агент по недвижимости может использовать следующую модель множественной линейной регрессии:
Цена недвижимости = β 0 + β 1 (площадь) + β 2 (одна семья) + β 3 (квартира)
Вот как мы будем интерпретировать коэффициенты модели:
- β 1 : Среднее изменение цены дома, связанное с одним дополнительным квадратным футом.
- β 2 : Средняя разница в цене между домом на одну семью и таунхаусом при условии, что площадь в квадратных футах остается постоянной.
- β 3 : Средняя разница в цене между частным домом и квартирой при условии постоянной площади.
Ознакомьтесь со следующими уроками, чтобы узнать, как создавать фиктивные переменные в различных статистических программах:
Дополнительные ресурсы
Следующие учебные пособия содержат подробное введение в модели ANOVA:
Следующие учебные пособия представляют собой углубленное введение в модели линейной регрессии: