Апостериорная вероятность: определение + пример

Апостериорная вероятность — это обновленная вероятность того, что событие произойдет после учета новой информации.

Например, нас может интересовать вероятность того, что событие «А» произойдет после учета только что произошедшего события «Б». Мы могли бы вычислить эту апостериорную вероятность, используя следующую формулу:

P(A|B) = P(A) * P(B|A) / P(B)

Золото:

P(A|B) = вероятность того, что событие A произойдет при условии, что событие B произошло. Обратите внимание, что «| » означает «данный».

P(A) = вероятность того, что событие A произойдет.

P(B) = вероятность того, что событие B произойдет.

P(B|A) = вероятность того, что событие B произойдет при условии, что событие A произошло.

Пример: вычисление апостериорной вероятности

Лес состоит на 20% из дубов и на 80% из клена. Предположим, мы знаем, что 90% дубов здоровы, тогда как здоровы только 50% кленов. Предположим, на расстоянии вы можете сказать, что конкретное дерево здорово. Какова вероятность того, что это дерево дуб?

Напомним, что вероятность того, что событие A произойдет при условии, что произошло событие B, равна:

P(A|B) = P(A) * P(B|A) / P(B)

В этом примере вероятность того, что это дерево — дуб, учитывая, что дерево здоровое, равна:

P(Дуб|Здоровый) = P(Дуб) * P(Здоровый|Дуб) / P(Здоровый)

P(Дуб) = Вероятность того, что данное дерево является дубом, равна 0,2, поскольку 20% всех деревьев в лесу — дубы.

P(Здоровое) = Вероятность того, что данное дерево здоровое, можно рассчитать следующим образом: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Healthy|Oak) = Вероятность того, что дерево здоровое, учитывая, что это дуб, равна 0,9 , поскольку нам сказали, что 90% дубов здоровы.

Используя эти три числа, мы можем найти вероятность того, что это дерево — дуб, при условии, что оно здоровое:

P(Дуб|Здоровый) = P(Дуб) * P(Здоровый|Дуб) / P(Здоровый) = (0,2) * (0,9) / (0,58) = 0,3103 .

Для интуитивного понимания этой вероятности предположим, что следующая сетка представляет собой лес из 100 деревьев. Ровно 20 деревьев — дубы, 18 из них здоровые. Остальные 80 деревьев — клены, из них 40 здоровые.

(O = Дуб, M = Клен, Зеленый = Здоровый, Красный = Нездоровый)

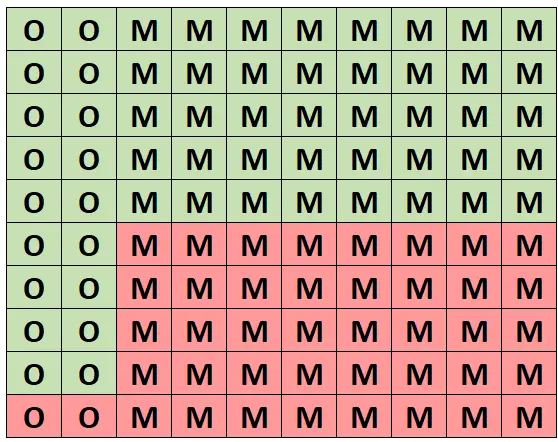
Из всех деревьев ровно 58 здоровых и 18 из них — дубы. Итак, если мы знаем, что выбрали здоровое дерево, то вероятность того, что это дуб, равна 18/58 = 0,3103 .

Когда следует использовать апостериорную вероятность?

Апостериорная вероятность используется в самых разных областях, включая финансы, медицину, экономику и прогнозирование погоды.

Смысл использования апостериорных вероятностей состоит в том, чтобы обновить наши предварительные убеждения о чем-то, как только мы получим новую информацию.

Напомним, из предыдущего примера мы знали, что вероятность того, что данное дерево в лесу — дуб, составляет 20%. Это называется априорной вероятностью . Если бы мы просто выбрали дерево наугад, мы знали, что вероятность того, что это дуб, равна 0,20.

Однако как только мы получили новую информацию о том, что выбранное нами дерево здоровое, мы смогли использовать эту новую информацию, чтобы определить, что апостериорная вероятность того, что это дерево является дубом, вместо этого составила 0,3103.

В реальном мире люди постоянно открывают новую информацию. Эта новая информация помогает нам обновить наши прежние убеждения. С точки зрения статистики это означает, что мы способны генерировать апостериорные вероятности происходящих событий, что помогает нам получить более точное понимание мира и позволяет нам делать более точные прогнозы о будущих событиях.