Как рассчитать асимметрию и эксцесс в r

В статистике асимметрия и эксцесс — это два способа измерения формы распределения.

Асимметрия — это мера асимметрии распределения. Это значение может быть положительным или отрицательным.

• Отрицательная асимметрия указывает на то, что хвост находится на левой стороне распределения и простирается в сторону более отрицательных значений.
• Положительный перекос указывает на то, что хвост находится на правой стороне распределения и простирается в сторону более положительных значений.
• Нулевое значение указывает на отсутствие асимметрии в распределении, а это означает, что распределение совершенно симметрично.

Куртозис — это мера того, является ли распределение тяжелым или легким по сравнению с нормальным распределением .

• Эксцесс нормального распределения равен 3.
• Если данное распределение имеет эксцесс меньше 3, его называют плейкуртическим , что означает, что оно имеет тенденцию давать все меньше и меньше экстремальных выбросов, чем нормальное распределение.
• Если данное распределение имеет эксцесс больше 3, оно называется лептокуртическим , что означает, что оно имеет тенденцию давать больше выбросов, чем нормальное распределение.

Примечание. Некоторые формулы (определение Фишера) вычитают 3 из эксцесса, чтобы облегчить сравнение с нормальным распределением. Используя это определение, распределение будет иметь больший эксцесс, чем нормальное распределение, если его значение эксцесса больше 0.

В этом руководстве объясняется, как рассчитать асимметрию и эксцесс заданного набора данных в R.

Пример: асимметрия и сглаживание в R

Предположим, у нас есть следующий набор данных:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Мы можем быстро визуализировать распределение значений в этом наборе данных, создав гистограмму:

 hist(data, col=' steelblue ') 

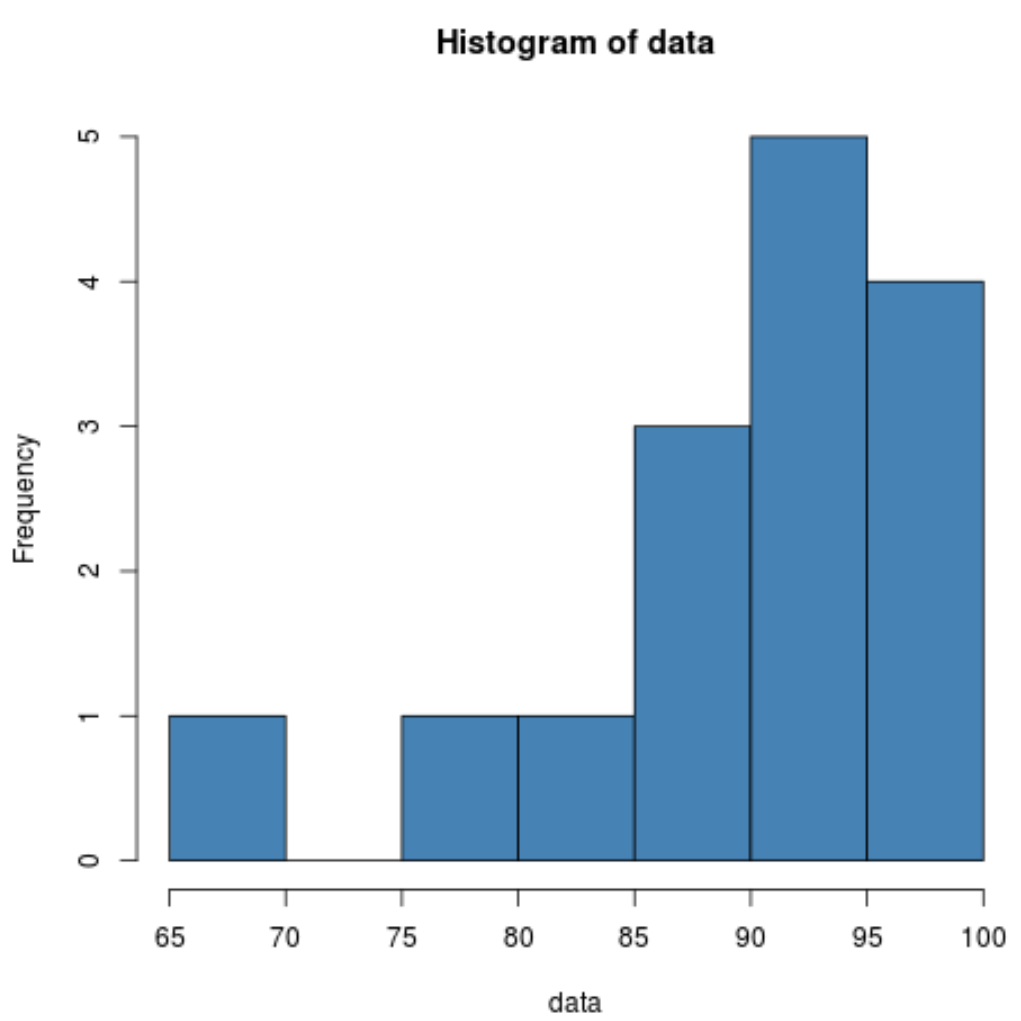
Гистограмма показывает нам, что распределение смещено влево. То есть большая часть значений сосредоточена в правой части распределения.

Чтобы вычислить асимметрию и эксцесс этого набора данных, мы можем использовать функции skewness() и kurtosis() из библиотеки moment в R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Асимметрия оказывается -1,391777 , а эксцесс — 4,177865 .

Поскольку асимметрия отрицательна, это указывает на то, что распределение искажено влево. Это подтверждает то, что мы видели на гистограмме.

Поскольку эксцесс больше 3, это указывает на то, что распределение имеет больше значений в хвостах по сравнению с нормальным распределением.

Библиотека моментов также предлагает функцию jarque.test() , которая выполняет тест на соответствие, определяющий, демонстрируют ли выборочные данные асимметрию и эксцесс, соответствующие нормальному распределению. Нулевая и альтернативная гипотезы этого теста следующие:

Нулевая гипотеза : набор данных имеет асимметрию и эксцесс, что соответствует нормальному распределению.

Альтернативная гипотеза : набор данных имеет асимметрию и эксцесс, которые не соответствуют нормальному распределению.

Следующий код показывает, как выполнить этот тест:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

P-значение теста оказывается равным 0,05756 . Поскольку это значение не меньше α = 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что этот набор данных имеет асимметрию и эксцесс, отличный от нормального распределения.

Полную документацию библиотеки Moments вы можете найти здесь .

Бонус: калькулятор асимметрии и эксцесса.

Вы также можете рассчитать асимметрию для данного набора данных с помощью калькулятора статистической асимметрии и эксцесса , который автоматически рассчитывает асимметрию и эксцесс для данного набора данных.