Распределение бернулли и биномиальное распределение: в чем разница?

Случайная величина подчиняется распределению Бернулли, если она имеет только два возможных результата: 0 или 1.

Например, предположим, что мы один раз подбрасываем монету. Пусть п . Это означает, что вероятность выпадения решки равна 1- p .

Итак, мы могли бы написать:

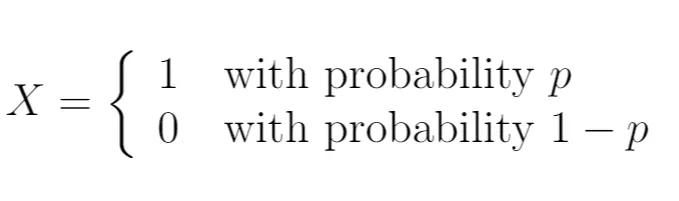
В этом случае случайная величина X подчиняется распределению Бернулли. Оно может принимать только два возможных значения.

Теперь, если мы подбросим монету несколько раз, сумма случайных величин Бернулли будет следовать биномиальному распределению.

Например, предположим, что мы подбрасываем монету 5 раз и хотим узнать вероятность того, что выпадет решка k раз. Похоже на случайную величину

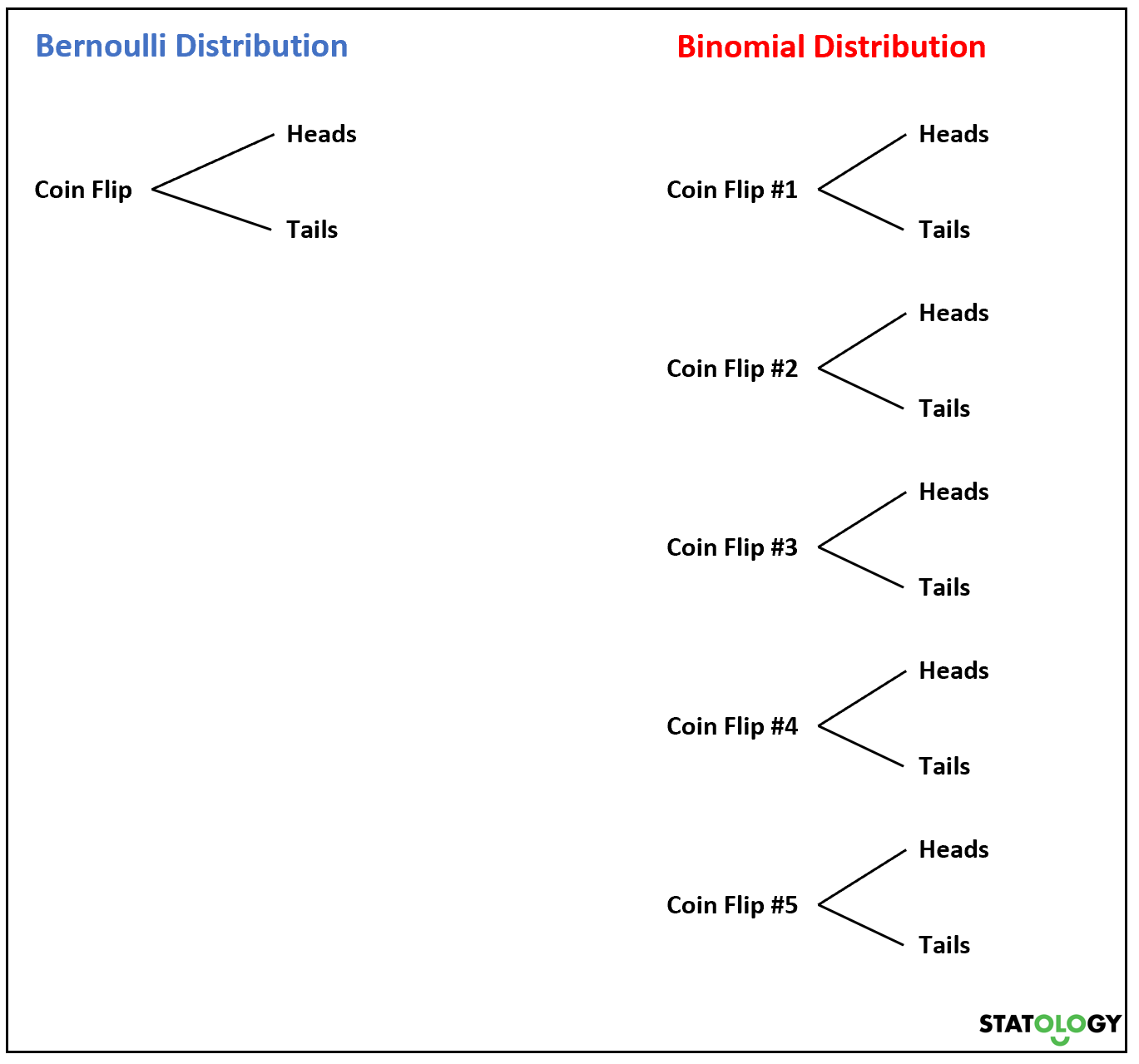
Если случайная величина X имеет биномиальное распределение, то вероятность того, что X = k успеха, можно найти по следующей формуле:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Золото:

• n: количество испытаний
• k: количество успехов
• p: вероятность успеха в данном испытании
• _n C _k : количество способов добиться k успехов в n испытаниях.

Например, предположим, что мы подбрасываем монету 3 раза. Мы можем использовать приведенную выше формулу, чтобы определить вероятность выпадения 0 орлов во время этих трех бросков:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Когда n = 1 испытание, биномиальное распределение эквивалентно распределению Бернулли.

Важные заметки

Вот несколько важных замечаний относительно распределения Бернулли и биномиального распределения:

1. Случайная величина, подчиняющаяся распределению Бернулли, может принимать только два возможных значения, а случайная величина, подчиняющаяся биномиальному распределению, может принимать несколько значений.

Например, при одном броске монеты у нас будет либо 0, либо 1 решка. Однако в серии из 5 розыгрышей у нас может быть 0, 1, 2, 3, 4 или 5 орлов.

2. Чтобы случайная величина имела биномиальное распределение, вероятность «успеха» в каждом испытании Бернулли должна быть одинаковой и независимой.

Например, если мы определяем «успех» как выпадение орла, то вероятность успеха при каждом броске равна 0,5 и каждый бросок независим – результат одного броска не влияет на результат другого.

Дополнительные ресурсы

Введение в биномиальные эксперименты
Введение в биномиальное распределение
Понимание формы биномиального распределения