Бета-распределение

К бенджамин андерсон 4 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое бета-дистрибутив и для чего он используется. Аналогичным образом вы сможете увидеть график бета-распределения и свойства этого типа распределения вероятностей.

Что такое бета-распределение?

Бета-распределение — это распределение вероятностей, определенное на интервале (0,1) и параметризованное двумя положительными параметрами: α и β. Другими словами, значения бета-распределения зависят от параметров α и β.

Поэтому основная особенность бета-распределения состоит в том, что его формой можно управлять с помощью параметров α и β. Кроме того, бета-распределение используется для определения случайных величин, значение которых находится между 0 и 1.

Существует несколько обозначений, указывающих на то, что непрерывная случайная величина определяется бета-распределением. Наиболее распространенными являются:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

В статистике бета-распределение имеет очень разнообразные применения. Например, бета-распределение используется для изучения процентных изменений в разных выборках. Аналогичным образом, в управлении проектами бета-распределение используется для проведения анализа Перта.

График бета-распределения

Учитывая определение бета-распределения, ниже показаны функция плотности и функция распределения вероятностей бета-распределения.

Ниже вы можете увидеть, как меняется график функции плотности бета-распределения в зависимости от параметров α и β.

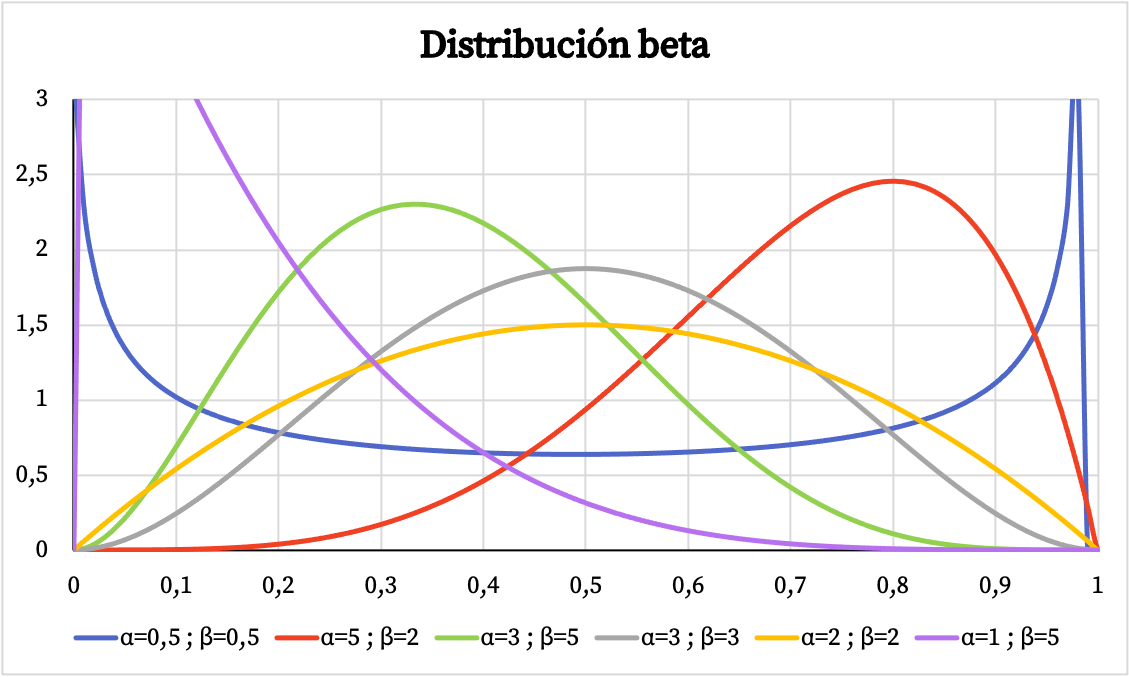
Аналогично, ниже вы можете увидеть графическое представление кумулятивной вероятности бета-распределения на основе параметров α и β.

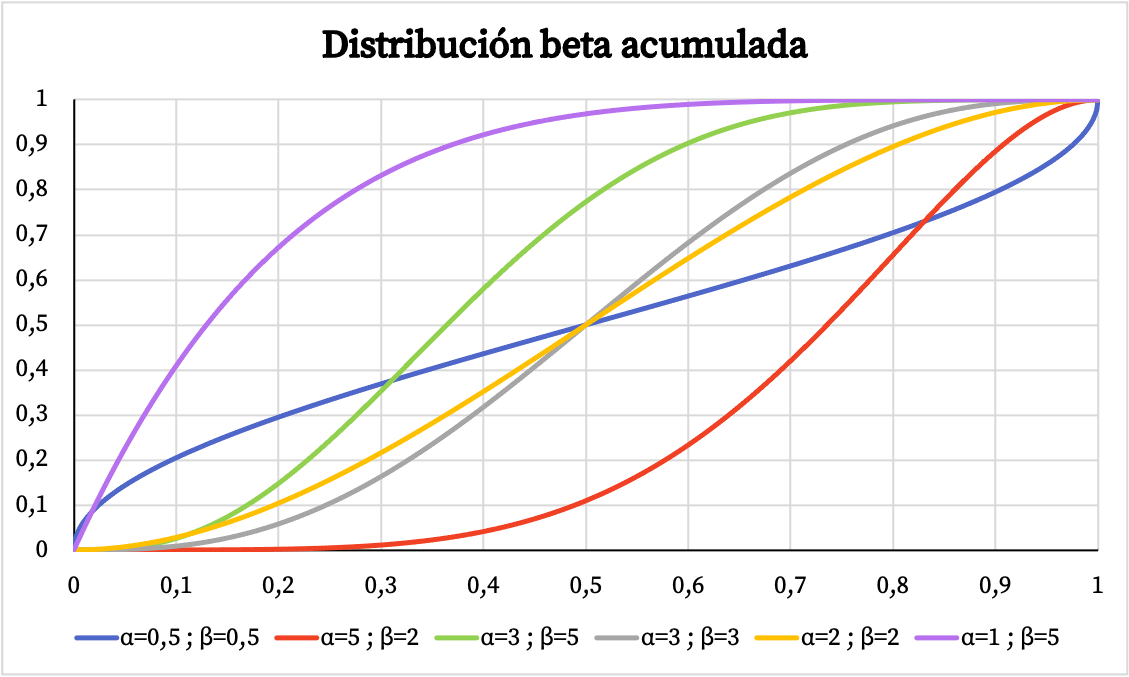
диаграмма распределения совокупной бета-версии

Характеристики бета-распределения

В этом разделе мы увидим, каковы наиболее важные характеристики бета-распределения.

Параметры α и β бета-распределения являются действительными и положительными числами.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}» title=»Rendered by QuickLaTeX.com» height=»54″ width=»44″ style=»vertical-align: 0px;»></p> </p> <ul> <li> Область бета-распределения находится в диапазоне от 0 до 1, два крайних значения не учитываются.</li> </ul> <p class=$ $x\in (0,1)$

Среднее значение бета-распределения равно альфа, деленному на сумму альфа плюс бета.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

Дисперсию бета-распределения можно рассчитать по следующей формуле:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Для значений альфа и бета больше 1 режим распределения бета можно легко найти с помощью следующего выражения:

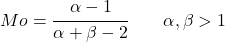
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=»Rendered by QuickLaTeX.com» height=»42″ width=»225″ style=»vertical-align: -16px;»></p> </p> <ul> <li> Плотность бета-распределения выглядит следующим образом:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Где B(α,β) — бета-функция, которая определяется как:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

Кумулятивная функция вероятности бета-распределения:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Где B(x;α,β) — неполная бета-функция, определяемая как:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Если X — переменная, определяемая бета-распределением, то 1-X — это переменная, определяемая бета-распределением, альфа- и бета-параметры которого являются бета- и альфа-параметрами исходного бета-распределения соответственно.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Если альфа- и бета-параметры бета-распределения равны 1, то распределение эквивалентно равномерному распределению параметров 0 и 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое бета-распределение?

График бета-распределения

Характеристики бета-распределения

Об авторе

бенджамин андерсон

Добавить комментарий