Как использовать биномиальное распределение в python
Биномиальное распределение является одним из наиболее часто используемых распределений в статистике. Он описывает вероятность получения k успехов в n биномиальных экспериментах.
Если случайная величина X имеет биномиальное распределение, то вероятность того, что X = k успеха, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
Золото:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
В этом руководстве объясняется, как использовать биномиальное распределение в Python.
Как создать биномиальное распределение
Вы можете сгенерировать массив значений, который соответствует биномиальному распределению, используя функцию random.binomial библиотеки numpy:
from numpy import random #generate an array of 10 values that follows a binomial distribution random.binomial(n=10, p=.25, size=10) array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])
Каждое число в итоговой таблице представляет количество «успехов», обнаруженных в ходе 10 испытаний, где вероятность успеха в данном испытании составляла 0,25 .
Как рассчитать вероятности, используя биномиальное распределение
Вы также можете ответить на вопросы о биномиальной вероятности, используя функцию binom библиотеки scipy.
Вопрос 1: Натан выполняет 60% штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он выполнит ровно 10?
from scipy.stats import binom #calculate binomial probability binom.pmf(k= 10 , n= 12 , p= 0.6 ) 0.0639
Вероятность того, что Натан выполнит ровно 10 штрафных бросков, равна 0,0639 .
Вопрос 2: Марти подбрасывает честную монету 5 раз. Какова вероятность того, что монета выпадет орлом 2 или менее раз?
from scipy.stats import binom #calculate binomial probability binom.cdf(k= 2 , n= 5 , p= 0.5 ) 0.5
Вероятность того, что монета выпадет орлом 2 раза или меньше, равна 0,5 .
Вопрос 3: Мы знаем, что 70% людей поддерживают определенный закон. Если случайным образом выбрано 10 человек, какова вероятность того, что от 4 до 6 из них поддержат закон?
from scipy.stats import binom #calculate binomial probability binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 ) 0.3398
Вероятность того, что от 4 до 6 случайно выбранных людей поддержат закон, равна 0,3398 .
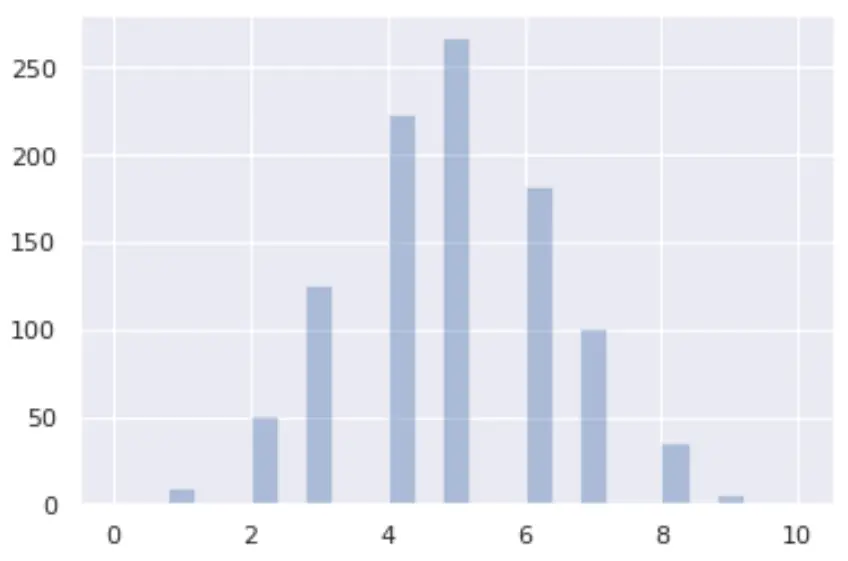
Как визуализировать биномиальное распределение
Вы можете визуализировать биномиальное распределение в Python, используя библиотеки seaborn и matplotlib :
from numpy import random import matplotlib.pyplot as plt import seaborn as sns x = random.binomial(n= 10 , p= 0.5 , size= 1000 ) sns.distplot(x, hist= True , kde= False ) plt.show()
Чай