Как выполнить коррекцию бонферрони в excel

Поправка Бонферрони относится к процессу корректировки уровня альфа (α) для семейства статистических тестов с целью контроля вероятности совершения ошибки первого рода.

Формула поправки Бонферрони выглядит следующим образом:

α _новый = α _{оригинальный} / n

Золото:

• _{исходный} α: Исходный уровень α.
• n: общее количество выполненных сравнений или тестов.

Например, если мы запускаем три статистических теста одновременно и хотим использовать α = 0,05 для каждого теста, поправка Бонферрони говорит нам, что мы должны использовать α _new = 0,01667 .

_новый α = _{исходный} α/n = 0,05/3 = 0,01667

Таким образом, нам следует отвергать нулевую гипотезу каждого отдельного теста только в том случае, если значение p теста меньше 0,01667.

Этот тип коррекции часто выполняется в апостериорных тестах после ANOVA, когда мы хотим одновременно сравнить несколько групповых средних.

В следующем пошаговом примере показано, как выполнить коррекцию Бонферрони после однофакторного дисперсионного анализа в Excel.

Шаг 1. Создайте данные

Во-первых, давайте создадим фальшивый набор данных, показывающий результаты студентов, которые использовали один из трех различных методов обучения для подготовки к экзамену:

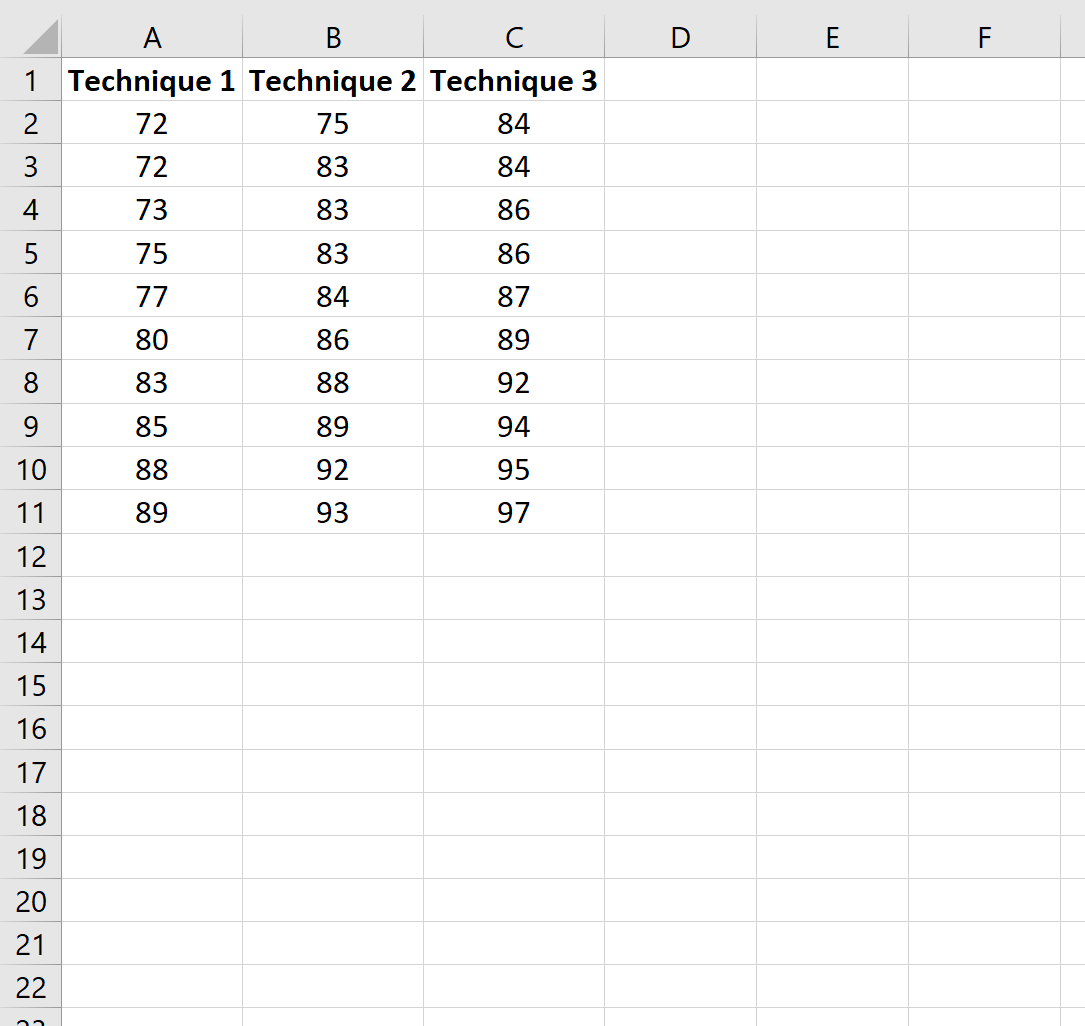
Шаг 2. Выполните однофакторный дисперсионный анализ.

Далее давайте выполним однофакторный дисперсионный анализ, чтобы определить, равны ли средние баллы на экзамене в трех группах.

Сначала выделите все данные, включая заголовки столбцов:

Затем щелкните вкладку «Данные» на верхней ленте, затем нажмите «Анализ данных »:

Если эта опция недоступна, необходимо сначала загрузить Analysis ToolPak .

В появившемся окне нажмите Anova: Single Factor и затем нажмите OK .

Заполните следующую информацию, затем нажмите «ОК» :

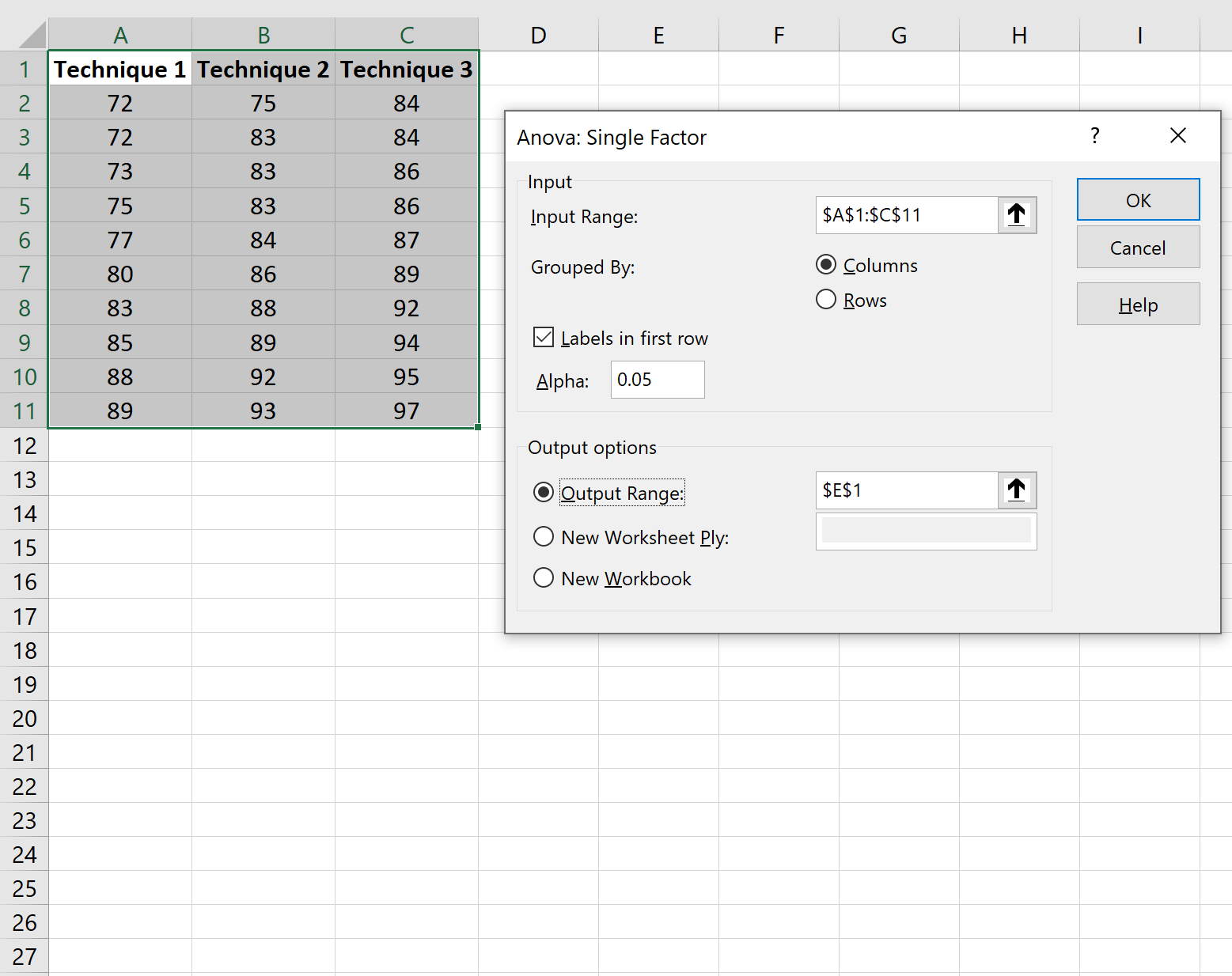
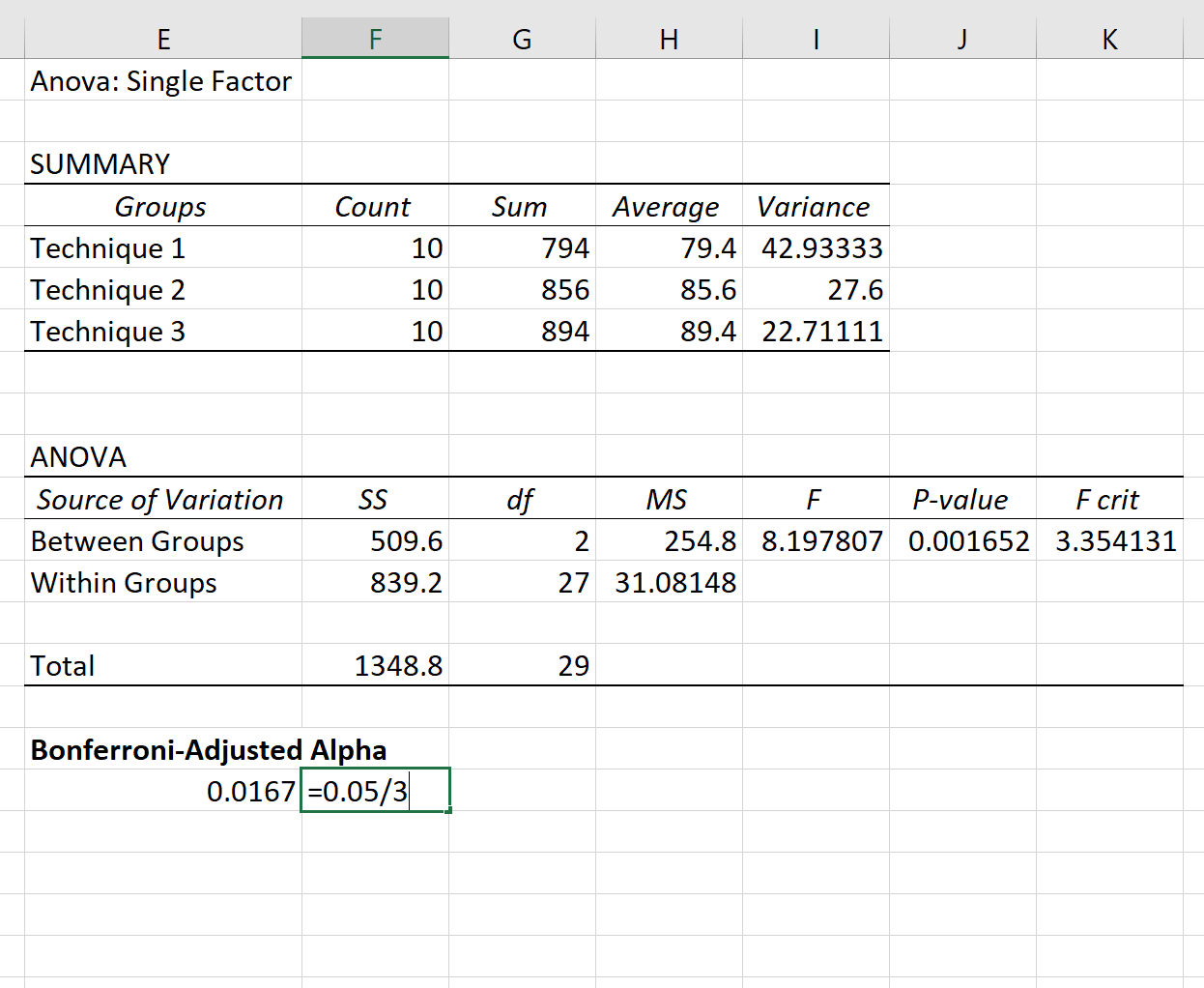
Результаты одностороннего дисперсионного анализа появятся автоматически:

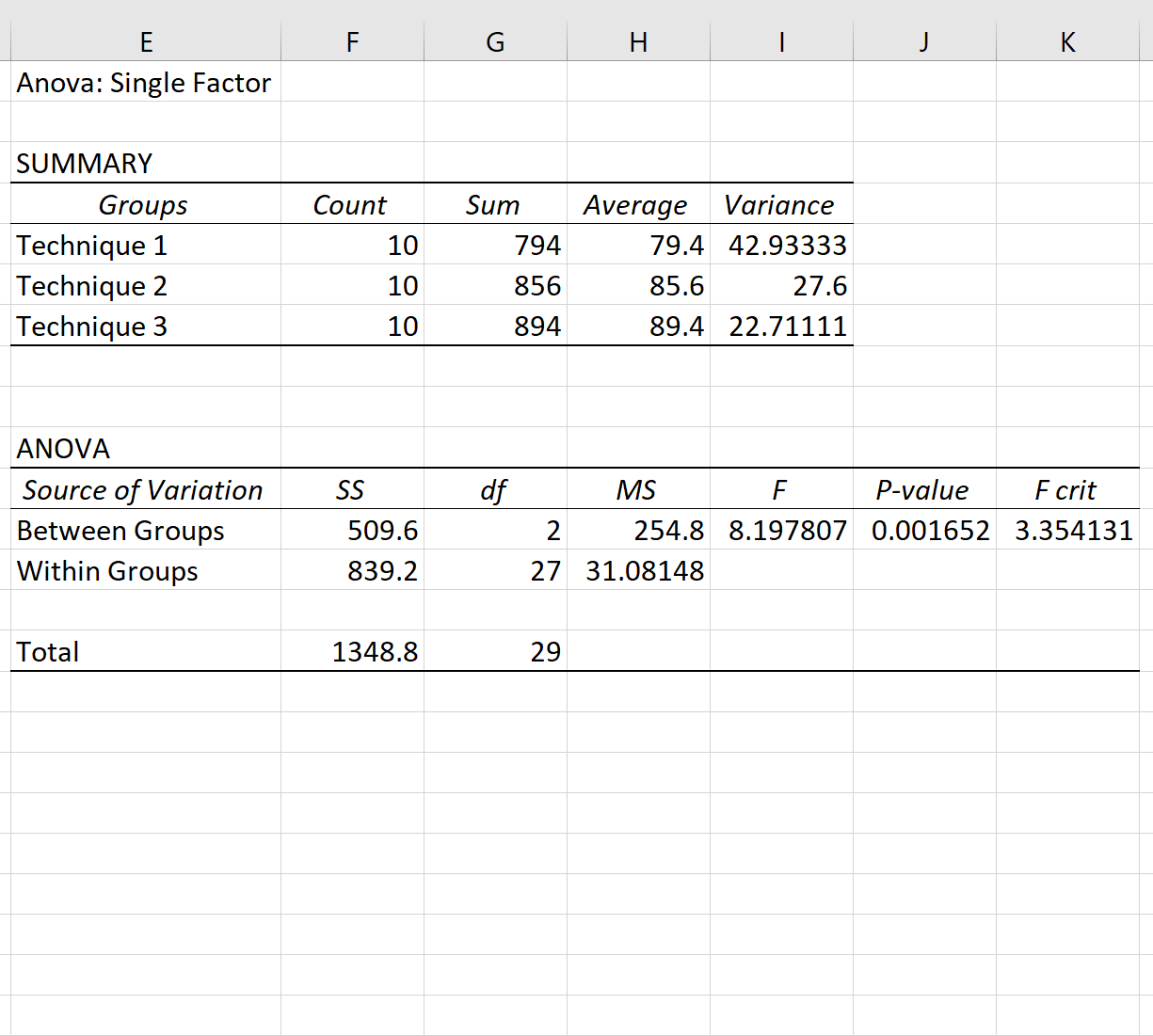
Напомним, что однофакторный дисперсионный анализ имеет следующие нулевые и альтернативные гипотезы:

• H ₀ (нулевая гипотеза): все средние значения группы равны.
• H _A (альтернативная гипотеза): по крайней мере одно групповое среднее отличается   отдых.

Поскольку значение p в таблице ANOVA (0,001652) меньше 0,05, у нас есть достаточно доказательств, чтобы отвергнуть нулевую гипотезу. Другими словами, средние баллы на экзаменах между тремя группами не равны.

Затем мы можем провести несколько сравнений, используя поправку Бонферрони между тремя группами, чтобы точно увидеть, какие групповые средние значения различаются.

Шаг 3. Выполните множественные сравнения, используя поправку Бонферрони.

Используя поправку Бонферрони, мы можем рассчитать скорректированный уровень альфа следующим образом:

α _новый = α _{оригинальный} / n

В нашем примере мы выполним следующие три сравнения:

• Техника 1 против Техники 2
• Техника 1 против Техники 3
• Техника 2 против Техники 3

Поскольку мы хотим использовать α = 0,05 для каждого теста, поправка Бонферрони говорит нам, что нам следует использовать α _new = 0,0167 .

Далее мы будем использовать t-тест для сравнения средних значений между каждой группой. В Excel вы можете использовать следующий синтаксис:

=TTEST(Таблица1, Таблица2, очереди=2, тип=2)

Золото:

• Array1: первый массив данных
• Array2: второй массив данных
• хвосты: количество хвостов в тесте. Мы будем использовать «2» для обозначения двустороннего теста.
• type: тип t-теста, который необходимо выполнить. Мы будем использовать «2» для обозначения t-критерия с равными дисперсиями.

На следующем снимке экрана показано, как выполнить каждый t-тест:

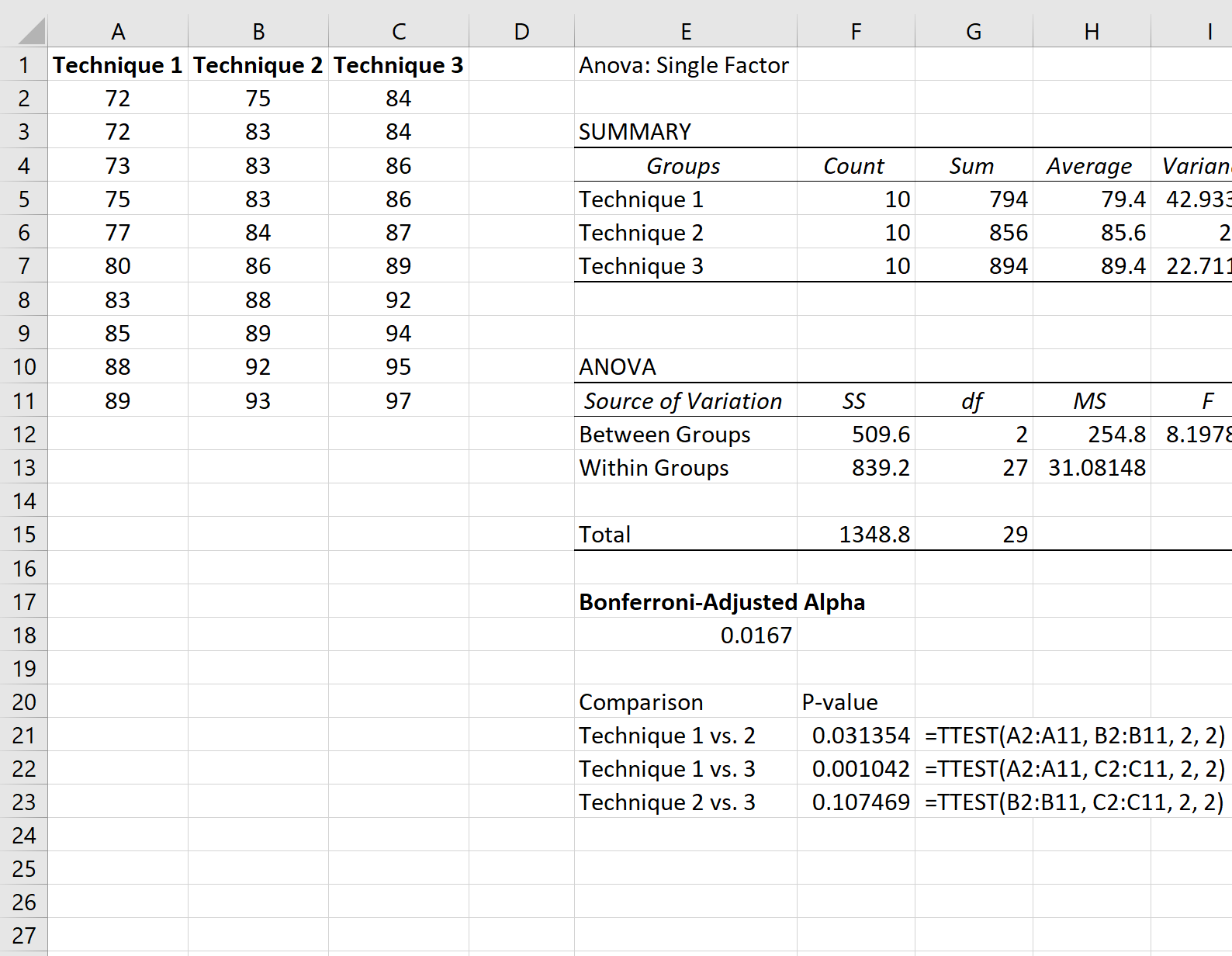
Единственное значение p ниже уровня альфа, скорректированного Бонферрони, получено в результате сравнения метода 1 и метода 2, значение p которого составило 0,001042 .

Таким образом, мы пришли к выводу, что только статистически значимая разница в средних баллах на экзамене была между Техникой 1 и Техникой 2.

Дополнительные ресурсы

Каков процент ошибок на семью?
Поправка Бонферрони: определение и пример
Калькулятор поправок Бонферрони