Как вычислить несходство брея-кертиса в r

Несходство Брея-Кёртиса — это способ измерения несходства между двумя разными сайтами.

Его часто используют в экологии и биологии для количественной оценки разницы между двумя участками с точки зрения видов, обитающих на этих участках.

Он рассчитывается следующим образом:

BC _ij знак равно 1 – (2*C _ij ) / (S _i + S _j )

Золото:

• C _ij : сумма наименьших значений для видов, обнаруженных на каждом участке.
• S _i : Общее количество образцов, подсчитанных на участке i.
• S _j : Общее количество образцов, подсчитанных на участке j.

Несходство Брея-Кёртиса всегда находится в диапазоне от 0 до 1, где:

• 0 означает, что два сайта не имеют различий. Другими словами, у них одинаковое количество представителей каждого типа видов.
• 1 указывает на то, что два сайта имеют полное несходство. Другими словами, они не имеют общих видов одного и того же типа.

Например, предположим, что ботаник выходит и подсчитывает количество пяти различных видов растений (A, B, C, D и E) на двух разных участках.

В следующей таблице суммированы собранные ею данные:

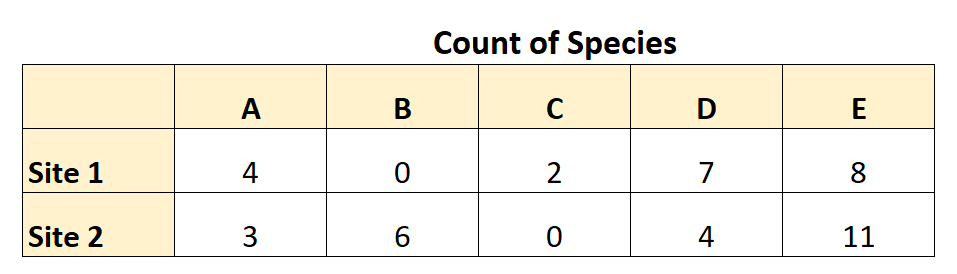
Используя эти данные, она может вычислить различие Брея-Кёртиса следующим образом:

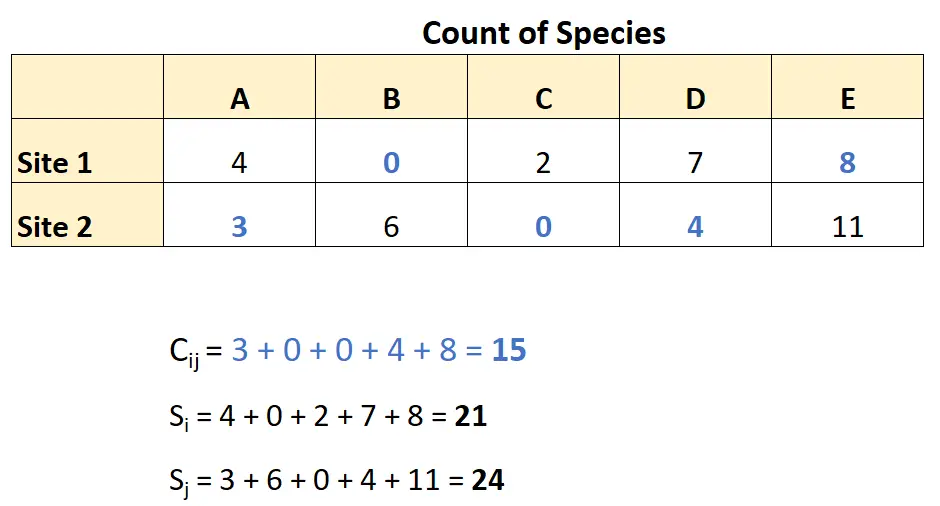
Интегрируя эти числа в формулу несходства Брея-Кёртиса, мы получаем:

• BC _ij знак равно 1 – (2*C _ij ) / (S _i + S _j )
• БК _ij = 1 – (2*15)/(21 + 24)
• БК _ij = 0,33

Различие Брея-Кертиса между этими двумя сайтами составляет 0,33 .

В следующем примере показано, как вычислить несходство Брея-Кертиса в R.

Пример: вычисление различия Брея-Кертиса в R

Во-первых, давайте создадим следующий фрейм данных в R для хранения наших значений данных:

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

Мы можем использовать следующий код для расчета различия Брея-Кертиса между двумя строками во фрейме данных:

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Коэффициент Брея-Кёртиса оказывается иным : 0,33 .

Это соответствует значению, которое мы рассчитали вручную ранее.

Примечание . Эта формула будет работать только в том случае, если каждая строка в фрейме данных представляет отдельный сайт.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать другие метрики сходства в R:

Как рассчитать сходство Жаккара в R
Как вычислить косинусное подобие в R