Внутригрупповые или межгрупповые вариации в anova
Однофакторный дисперсионный анализ используется для определения того, равны ли средние значения трех или более независимых групп.
Однофакторный дисперсионный анализ использует следующие нулевые и альтернативные гипотезы :
- H 0 : Все средние значения группы равны.
- Х А : По крайней мере, одно среднее значение группы отличается от других.
Каждый раз, когда вы выполняете однофакторный дисперсионный анализ, вы получаете сводную таблицу, которая выглядит следующим образом:
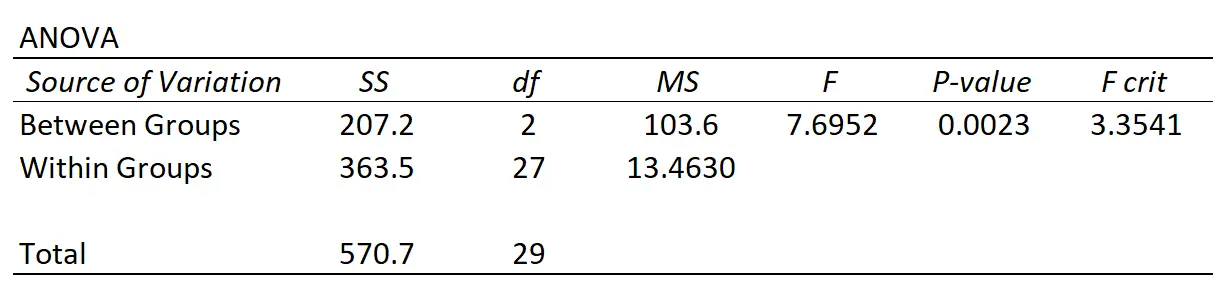
Мы видим, что существует два разных источника вариаций, которые измеряет ANOVA:
Разница между группами : общая разница между средним значением каждой группы и общим средним значением.
Внутригрупповая вариация : общая вариация индивидуальных значений в каждой группе и их среднее по группе.
Если различия между группами высоки по сравнению с различиями внутри группы, то статистика F дисперсионного анализа будет выше, а соответствующее значение p будет ниже, что повышает вероятность отклонения нулевой гипотезы, согласно которой групповые средства равны.
В следующем примере показано, как на практике рассчитать вариацию между группами и внутри группы для однофакторного дисперсионного анализа.
Пример: расчет вариации внутри группы и между группами в ANOVA
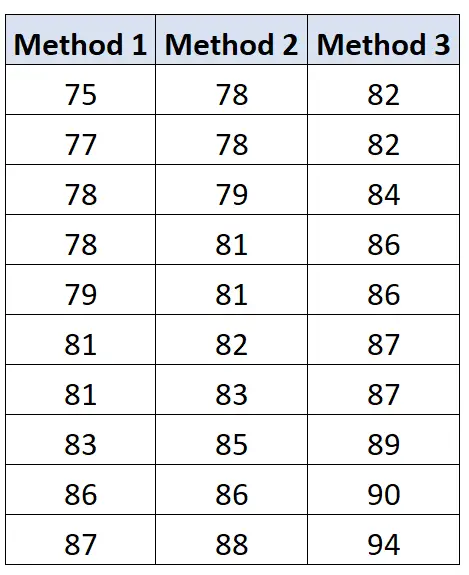
Предположим, мы хотим определить, приводят ли три разных метода обучения к разным средним баллам на экзамене. Чтобы проверить это, мы набираем 30 студентов и случайным образом распределяем по 10 каждому, чтобы они использовали разные методы обучения.
Результаты экзаменов студентов каждой группы представлены ниже:
Мы можем использовать следующую формулу для расчета разницы между группами :
Разница между группами = Σn j (X j – X ..) 2
Золото:
- n j : размер выборки группы j
- Σ : символ, означающий «сумма».
- X j : среднее значение группы j
- X .. : общий средний показатель
Чтобы рассчитать это значение, мы сначала рассчитаем среднее значение каждой группы и общее среднее значение:
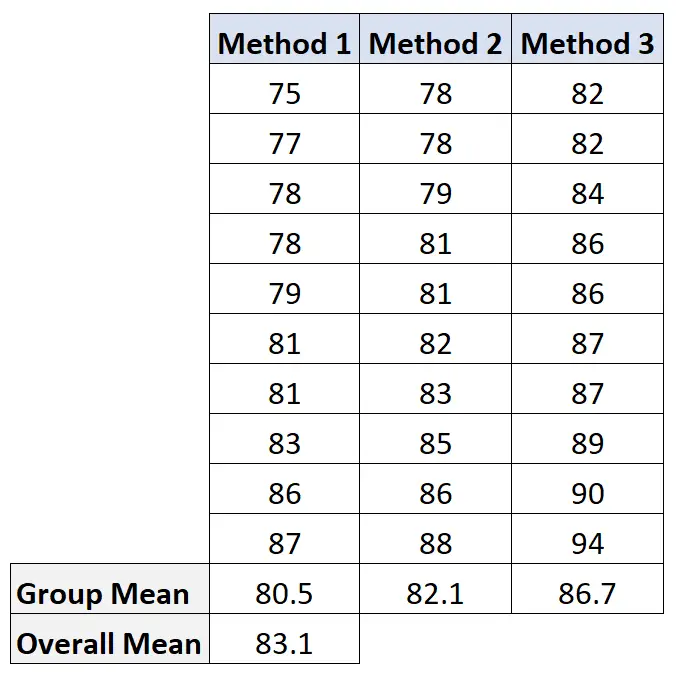
Затем мы вычисляем разницу между группами следующим образом: 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Затем мы можем использовать следующую формулу для расчета вариации внутри группы :
Внутригрупповая вариация : Σ(X ij – X j ) 2
Золото:
- Σ : символ, означающий «сумма».
- X ij : i-е наблюдение группы j
- X j : среднее значение группы j
В нашем примере мы рассчитываем вариацию внутри группы как:
1-я группа: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2 + (78-80,5) 2 + (79-80,5) 2 + (81-80,5) 2 + (81-80,5) 2 + (83-80,5) 2 + (86-80,5) 2 + (87-80,5) 2 = 136,5
Группа 2: (78-82,1) 2 + (78-82,1) 2 + (79-82,1) 2 + (81-82,1) 2 + (81-82,1) 2 + (82-82,1) 2 + (83-82,1) 2 + (85-82,1) 2 + (86-82,1) 2 + (88-82,1) 2 = 104,9
Группа 3: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2 + (86-86,7) 2 + (86-86,7) 2 + (87-86,7) 2 + (87-86,7) 2 + (89-86,7) 2 + (90-86,7) 2 + (94-86,7) 2 = 122,1
Разброс внутри группы: 136,5 + 104,9 + 122,1 = 363,5.
Если мы используем статистическое программное обеспечение для выполнения однофакторного дисперсионного анализа с использованием этого набора данных, мы получим следующую таблицу дисперсионного анализа:
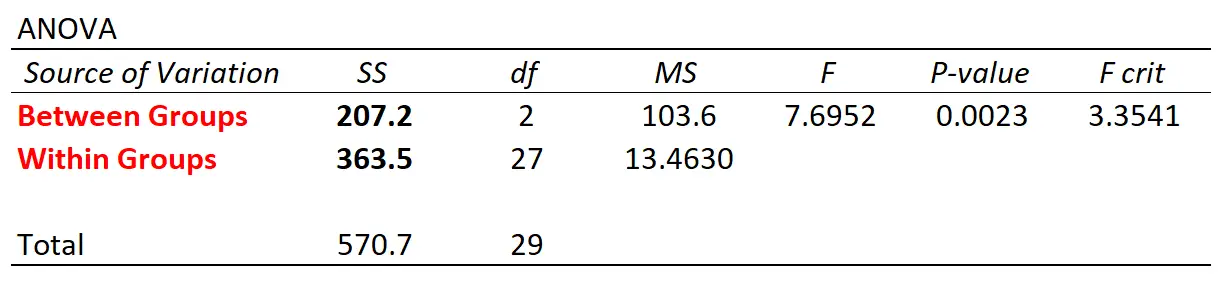
Обратите внимание, что значения вариаций между группами и внутри группы совпадают с теми, которые мы рассчитали вручную.
Общая статистика F в таблице — это способ количественной оценки взаимосвязи между вариациями между группами и вариациями внутри группы.
Чем больше статистика F, тем больше средние различия между группами по сравнению с различиями внутри групп.
Таким образом, чем больше статистика F, тем очевиднее существует разница между групповыми средними.
В этом примере мы видим, что значение p, соответствующее F-статистике 7,6952, равно 0,0023 .
Поскольку это значение меньше α = 0,05, мы отвергаем нулевую гипотезу ANOVA и приходим к выводу, что три метода исследования не приводят к одинаковому результату на экзамене.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о моделях ANOVA:
Введение в однофакторный дисперсионный анализ
Как интерпретировать значение F и значение P в ANOVA
Полное руководство: Как сообщить о результатах ANOVA
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше