Как выполнить однофакторный дисперсионный анализ в spss

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

Этот тип теста называется однофакторным дисперсионным анализом, поскольку мы анализируем влияние предикторной переменной на переменную отклика.

Если бы нас вместо этого интересовало влияние двух переменных-предсказателей на переменную отклика, мы могли бы выполнить двусторонний дисперсионный анализ .

В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ в SPSS.

Пример. Односторонний дисперсионный анализ в SPSS.

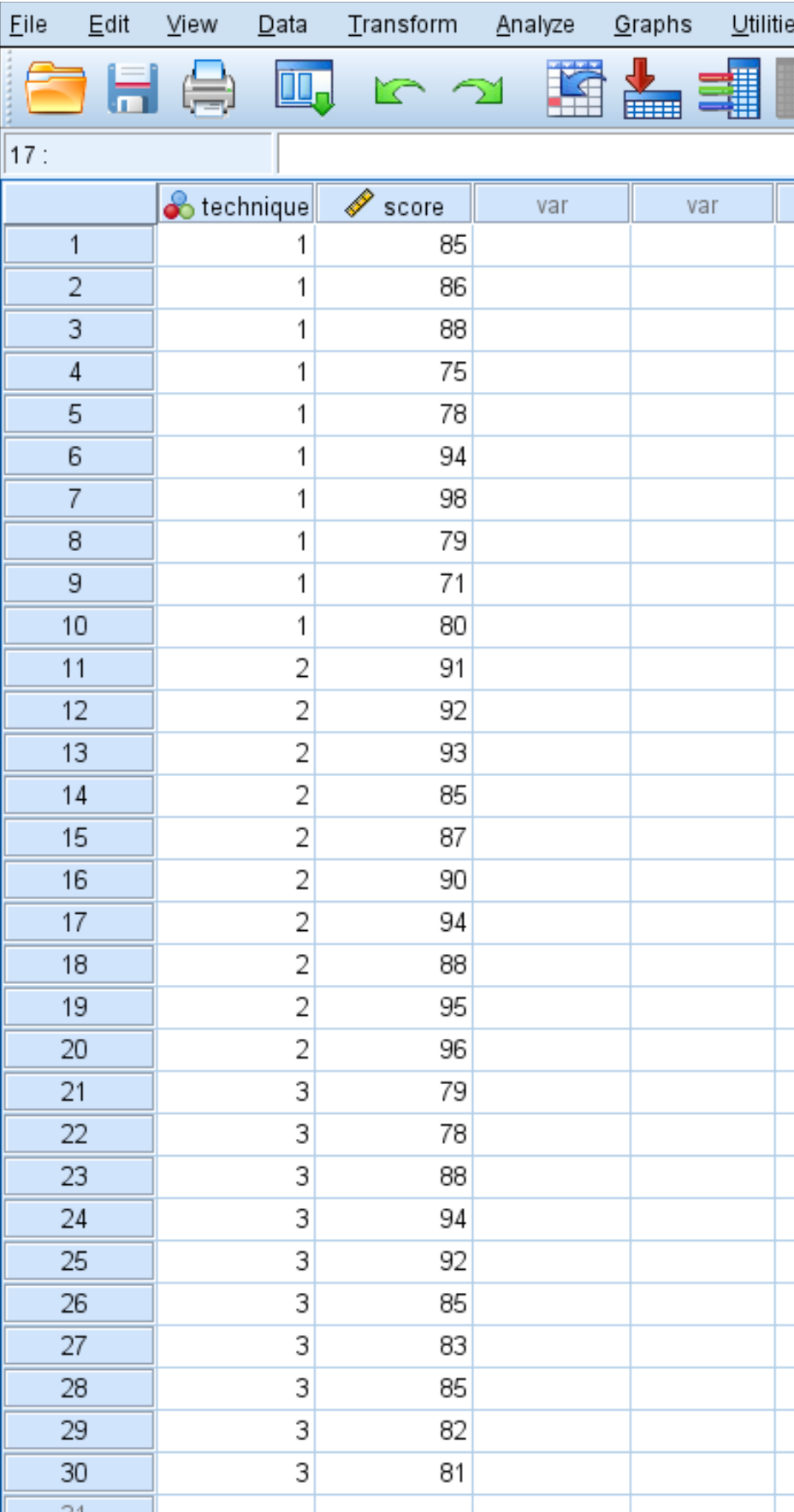
Предположим, исследователь набирает 30 студентов для участия в исследовании. Студентам случайным образом назначаются использовать один из трех методов обучения в следующем месяце для подготовки к экзамену. В конце месяца все студенты сдают один и тот же тест.

Результаты тестирования учащихся показаны ниже:

Используйте следующие шаги, чтобы выполнить однофакторный дисперсионный анализ и определить, одинаковы ли средние баллы в трех группах.

Шаг 1: Визуализируйте данные.

Сначала мы создадим коробчатые диаграммы , чтобы визуализировать распределение результатов тестов по каждому из трех методов обучения. Откройте вкладку «Диаграммы» , затем нажмите «Построитель диаграмм» .

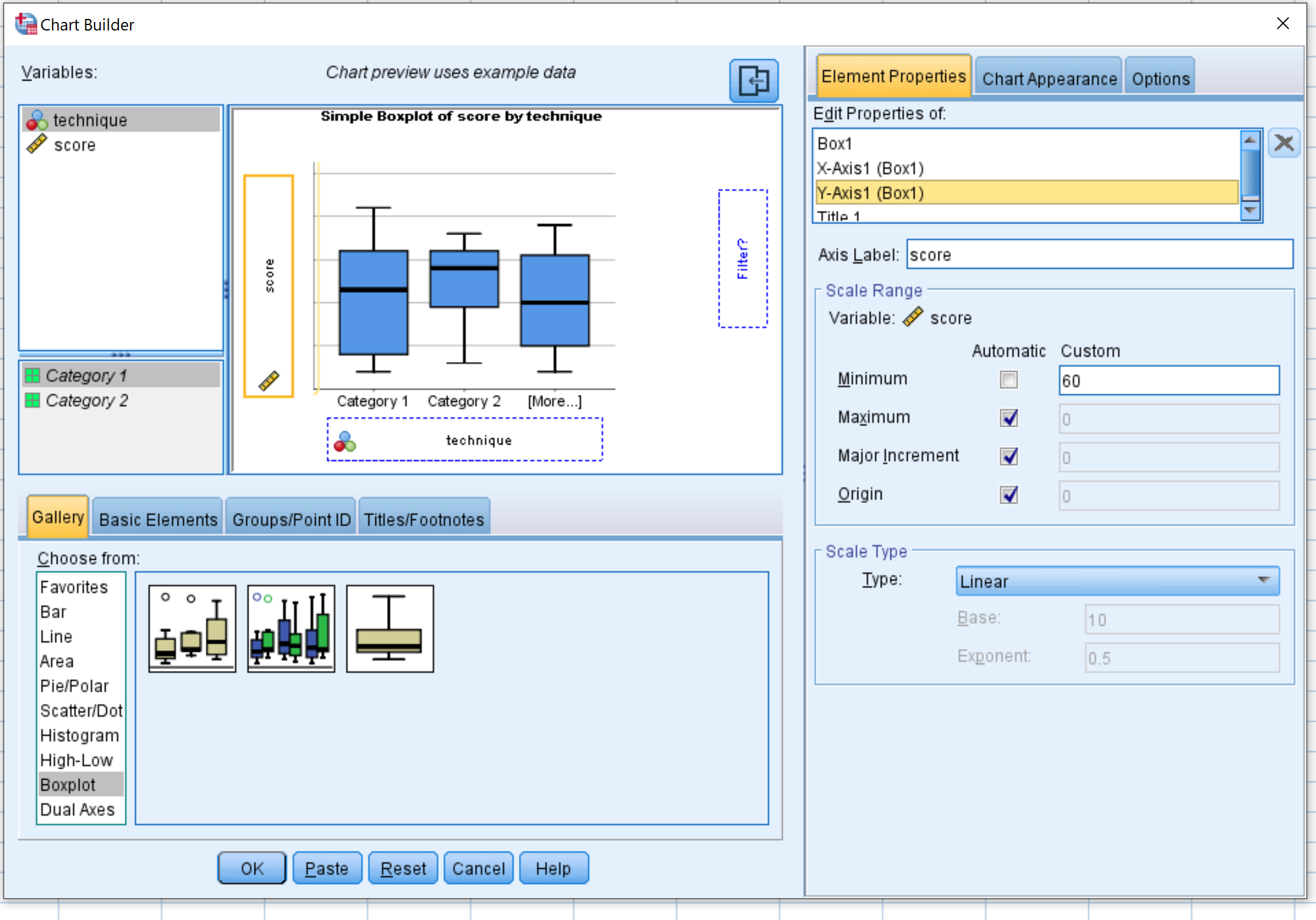
Выберите Boxplot в окне «Выбрать из: ». Затем перетащите первую диаграмму с надписью Simple Boxplot в главное окно редактирования. Перетащите техническую переменную по оси X, а оценку — по оси Y.

Затем нажмите «Свойства элемента» , затем нажмите «Ось Y1» . Измените минимальное значение на 60. Затем нажмите «ОК» .

Появятся следующие коробчатые диаграммы:

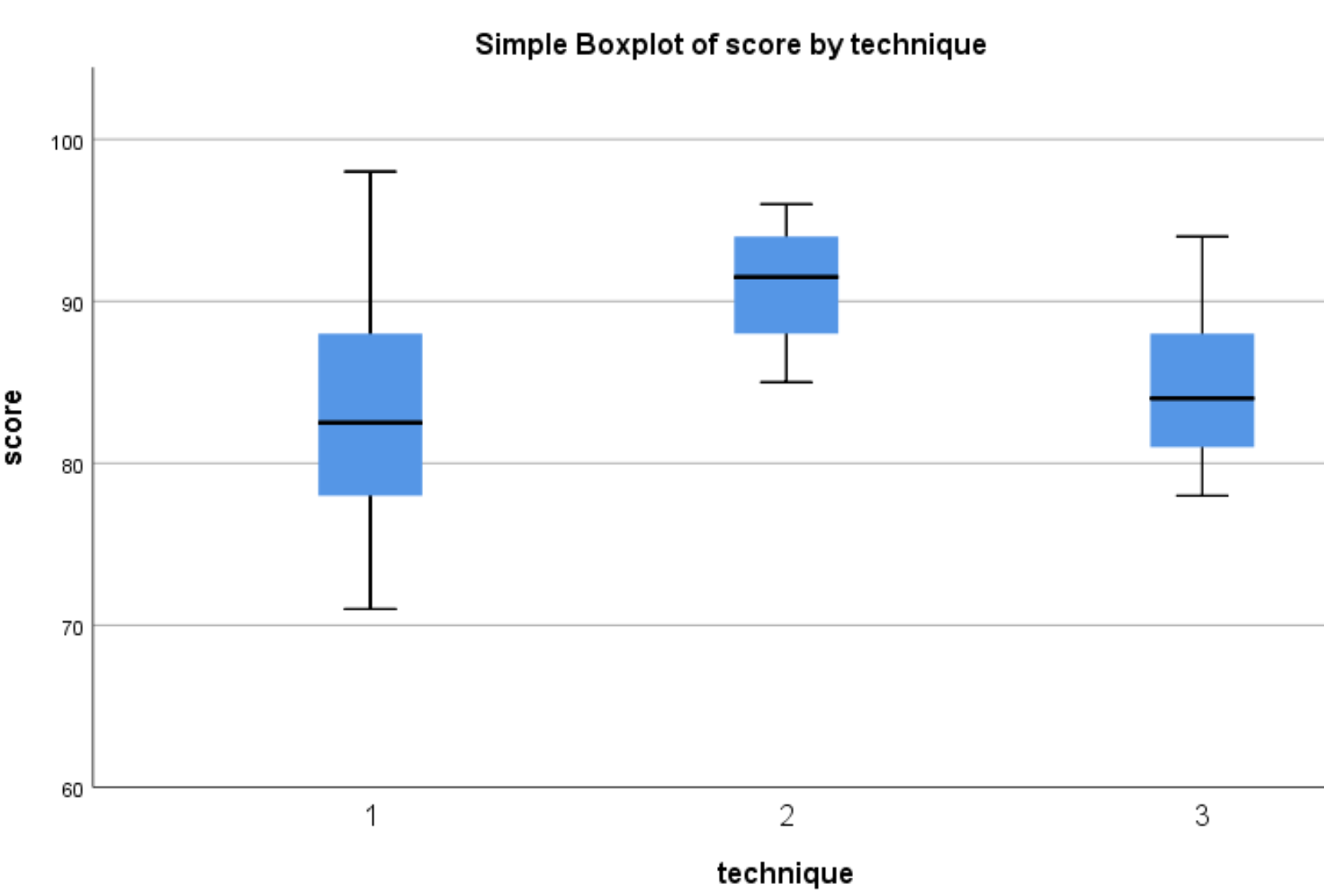
Мы видим, что распределение результатов тестов имеет тенденцию быть выше у студентов, которые использовали метод 2, чем у студентов, которые использовали методы 1 и 3. Чтобы определить, являются ли эти различия в баллах статистически значимыми, мы выполним однофакторный дисперсионный анализ.

Шаг 2: Выполните односторонний дисперсионный анализ.

Откройте вкладку «Анализ» , затем «Сравнить средние» , затем «Односторонний дисперсионный анализ» .

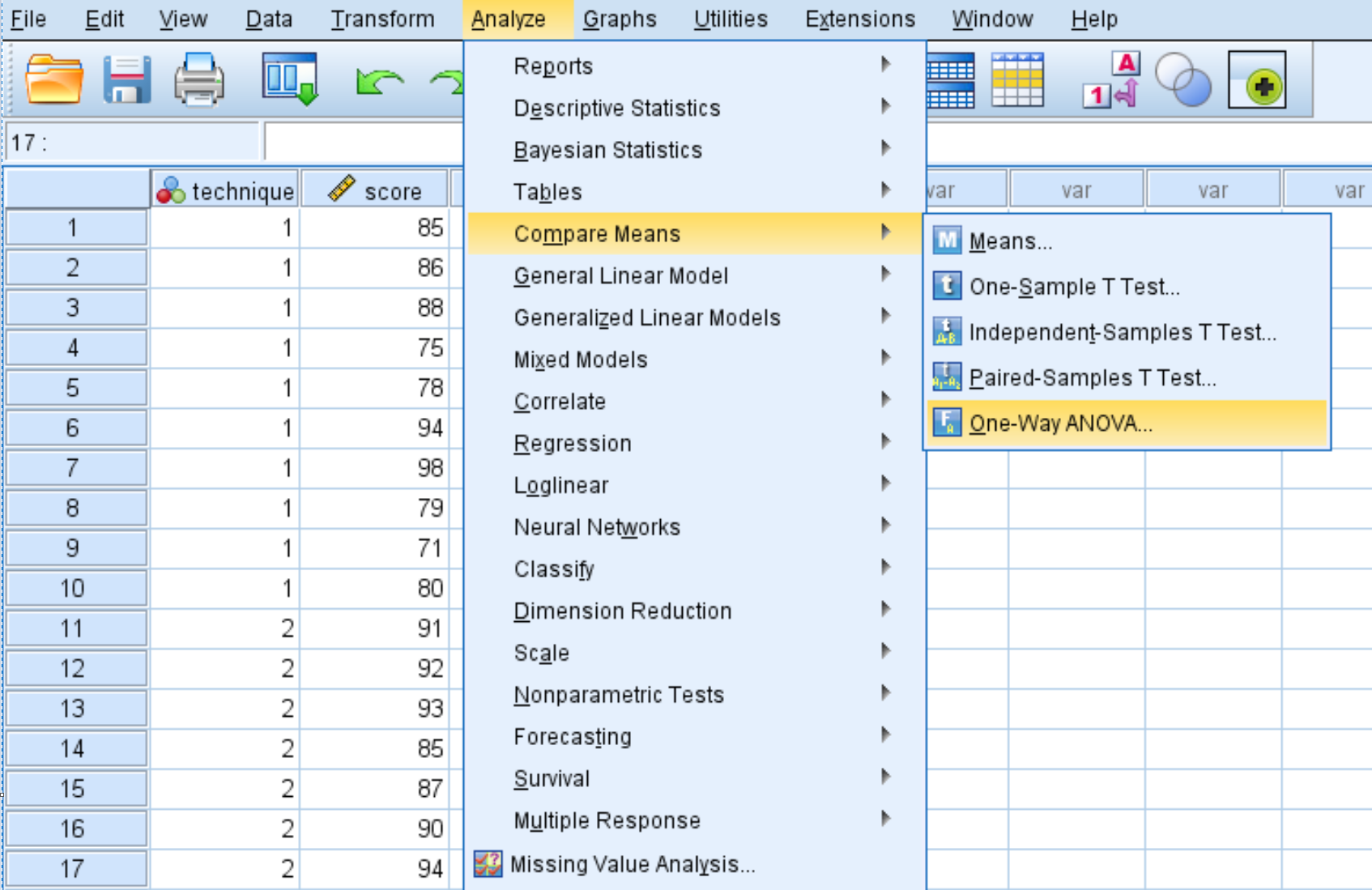
В появившемся новом окне поместите переменную оценку в поле «Зависимый список», а метод переменной — в поле «Фактор».

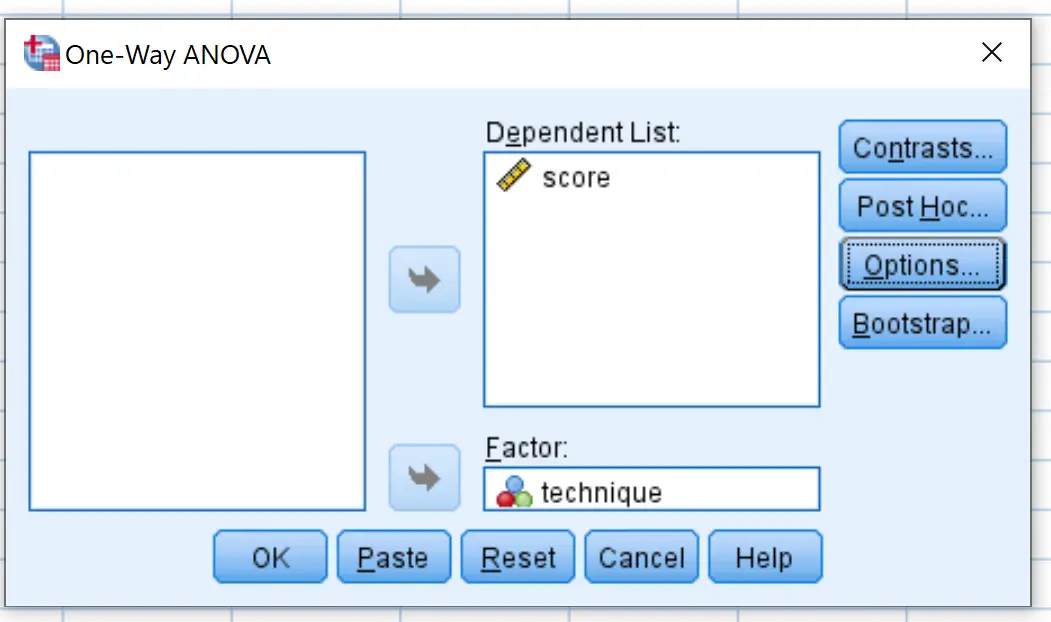
Затем нажмите Post Hoc и установите флажок рядом с Tukey . Затем нажмите Продолжить .

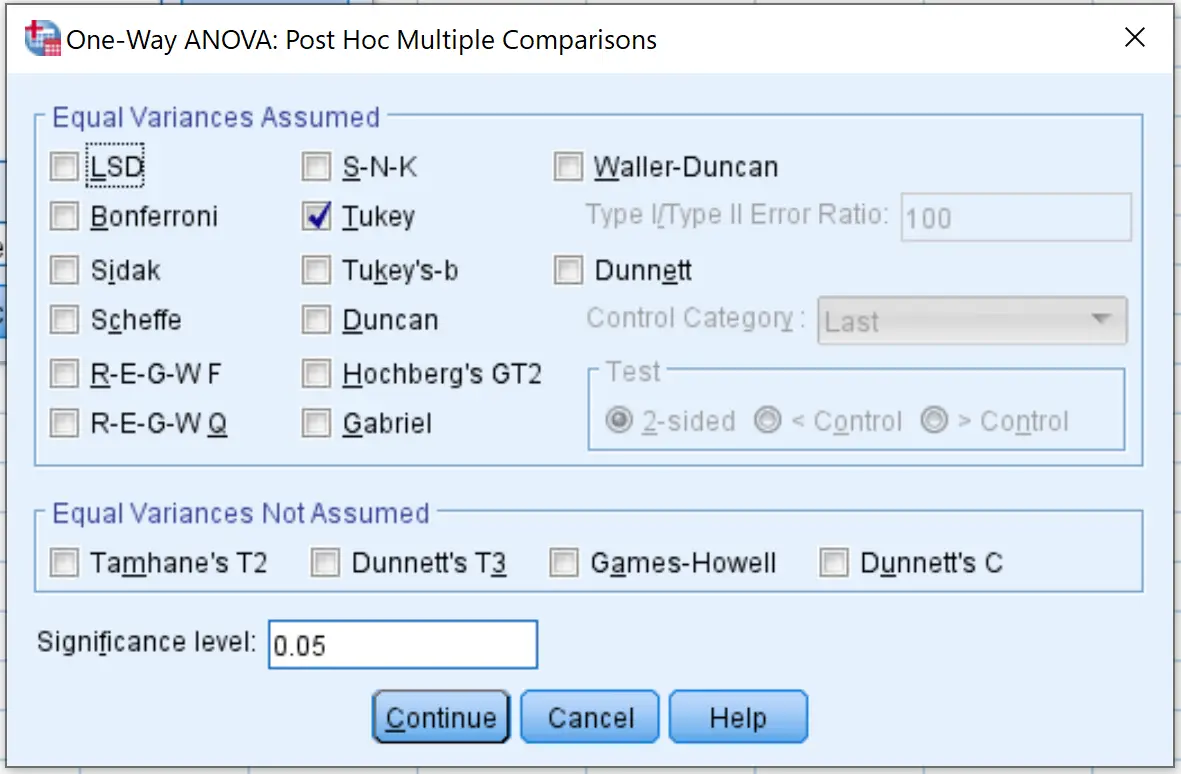
Затем нажмите «Параметры» и установите флажок «Описательный» . Затем нажмите Продолжить .

Наконец, нажмите ОК .

Шаг 3: Интерпретируйте результат.

Как только вы нажмете «ОК» , появятся результаты одностороннего дисперсионного анализа. Вот как интерпретировать результат:

Описание таблицы

В этой таблице представлена описательная статистика для каждой из трех групп в нашем наборе данных.

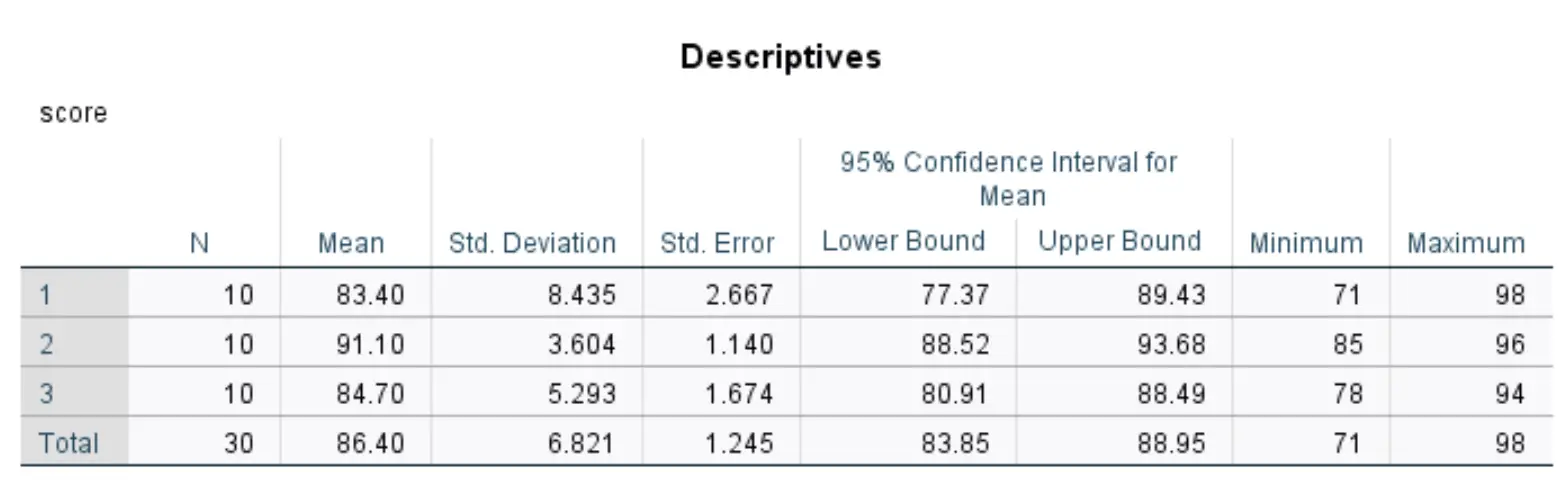
Наиболее значимые цифры включают в себя:

• N: Количество студентов в каждой группе.
• Среднее: средний балл теста для каждой группы.
• Стандарт. Отклонение: Стандартное отклонение результатов испытаний для каждой группы.

Таблица дисперсионного анализа

В этой таблице показаны результаты однофакторного дисперсионного анализа:

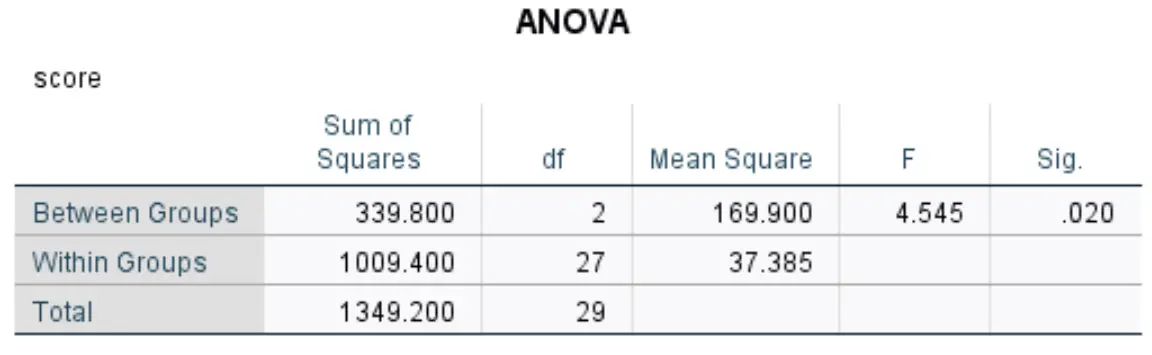
Наиболее значимые цифры включают в себя:

• F: Общая статистика F.
• Sig: значение p, соответствующее статистике F (4,545) с числителем df (2) и знаменателем df (27). В этом случае значение p оказывается равным 0,020 .

Напомним, что однофакторный дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:

• H ₀ (нулевая гипотеза): μ ₁ = μ ₂ = μ ₃ = … = μ _k (все средние значения совокупности равны)
• H _A (альтернативная гипотеза): по крайней мере одно среднее значение популяции отличается   отдых

Поскольку значение p таблицы ANOVA меньше 0,05, у нас есть достаточно доказательств, чтобы отвергнуть нулевую гипотезу и сделать вывод, что по крайней мере одно из групповых средних значений отличается от других.

Чтобы точно узнать, какие групповые средние отличаются друг от друга, мы можем обратиться к последней таблице результатов ANOVA.

Таблица множественного сравнения

В этой таблице показаны апостериорные множественные сравнения Тьюки между каждой из трех групп. Нас в основном интересует Сиг. столбец, в котором отображаются значения p для различий в средних значениях между каждой группой:

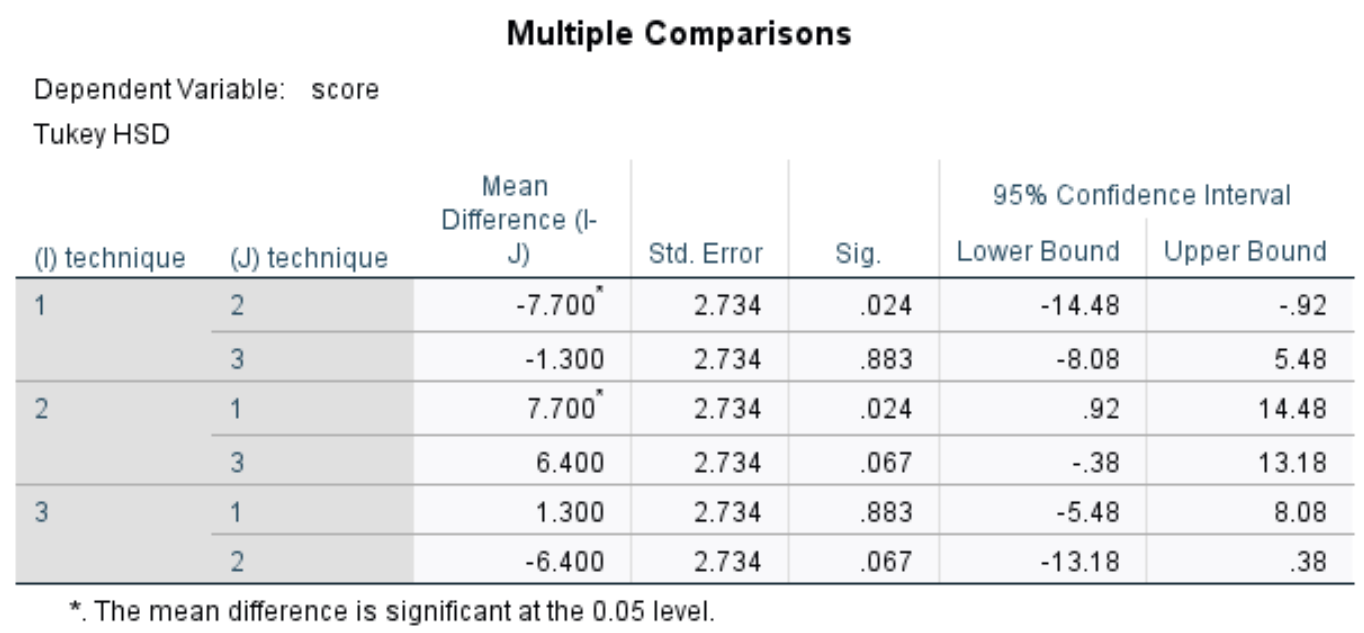
В таблице мы можем увидеть значения p для следующих сравнений:

• Техника 1 против 2: | р-значение = 0,024
• Техника 1 против 3 | p-значение = 0,883
• Техника 2 против 3 | р-значение = 0,067

Единственное групповое сравнение со значением p менее 0,05 происходит между Методикой 1 и Методом 2.

Это говорит нам о том, что существует статистически значимая разница в средних результатах тестов между студентами, использовавшими Методику 1, и теми, кто использовал Методику 2.

Однако статистически значимой разницы между методами 1 и 3, а также между методами 2 и 3 нет.

Шаг 4: Сообщите о результатах.

Наконец, мы можем сообщить о результатах одностороннего дисперсионного анализа. Вот пример того, как это сделать:

Был проведен однофакторный дисперсионный анализ, чтобы определить, привели ли три разных метода исследования к различным результатам испытаний.

В общей сложности 10 студентов использовали каждый из трех методов обучения в течение месяца, прежде чем сдать один и тот же тест.

Однофакторный дисперсионный анализ показал, что существует статистически значимая разница в результатах тестов как минимум между двумя группами (F(2, 27) = 4,545, p = 0,020).

Тест Тьюки для множественных сравнений показал, что средние баллы по тесту значительно различались между студентами, которые использовали метод 1 и метод 2 (p = 0,024, 95% ДИ = [-14,48, -0,92]).

Не было статистически значимой разницы между баллами по методикам 1 и 3 (р = 0,883) или между баллами по методикам 2 и 3 (р = 0,067).