Как выполнить односторонний дисперсионный анализ в sas

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

В этом руководстве представлен пошаговый пример выполнения одностороннего дисперсионного анализа в SAS.

Шаг 1. Создайте данные

Предположим, исследователь набирает 30 студентов для участия в исследовании. Студентам случайным образом назначаются использовать один из трех методов обучения для подготовки к экзамену.

Результаты экзамена для каждого студента показаны ниже:

Мы можем использовать следующий код для создания этого набора данных в SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Шаг 2. Выполните однофакторный дисперсионный анализ.

Далее мы будем использовать процедуру ANOVA для выполнения одностороннего дисперсионного анализа:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

Примечание . Мы использовали функцию среднего , чтобы указать, что апостериорный тест Тьюки следует выполнять, если общее значение p из однофакторного дисперсионного анализа является статистически значимым.

Шаг 3: Интерпретируйте результаты

Первая таблица, которую мы хотим проанализировать в результатах, — это таблица ANOVA:

Из этой таблицы мы видим:

• Общее значение F: 5,26
• Соответствующее значение p: 0,0140.

Напомним, что однофакторный дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:

• H ₀ : Все средние значения группы равны.
• H _A : По крайней мере одно среднее значение группы отличается   отдых.

Поскольку значение p таблицы ANOVA (0,0140) меньше α = 0,05, мы отвергаем нулевую гипотезу.

Это говорит нам о том, что средний балл на экзамене не одинаков для всех трех методов обучения.

Связанный: Как интерпретировать F-значение и P-значение в ANOVA

SAS также предоставляет коробчатые диаграммы для визуализации распределения результатов экзаменов по каждому из трех методов обучения:

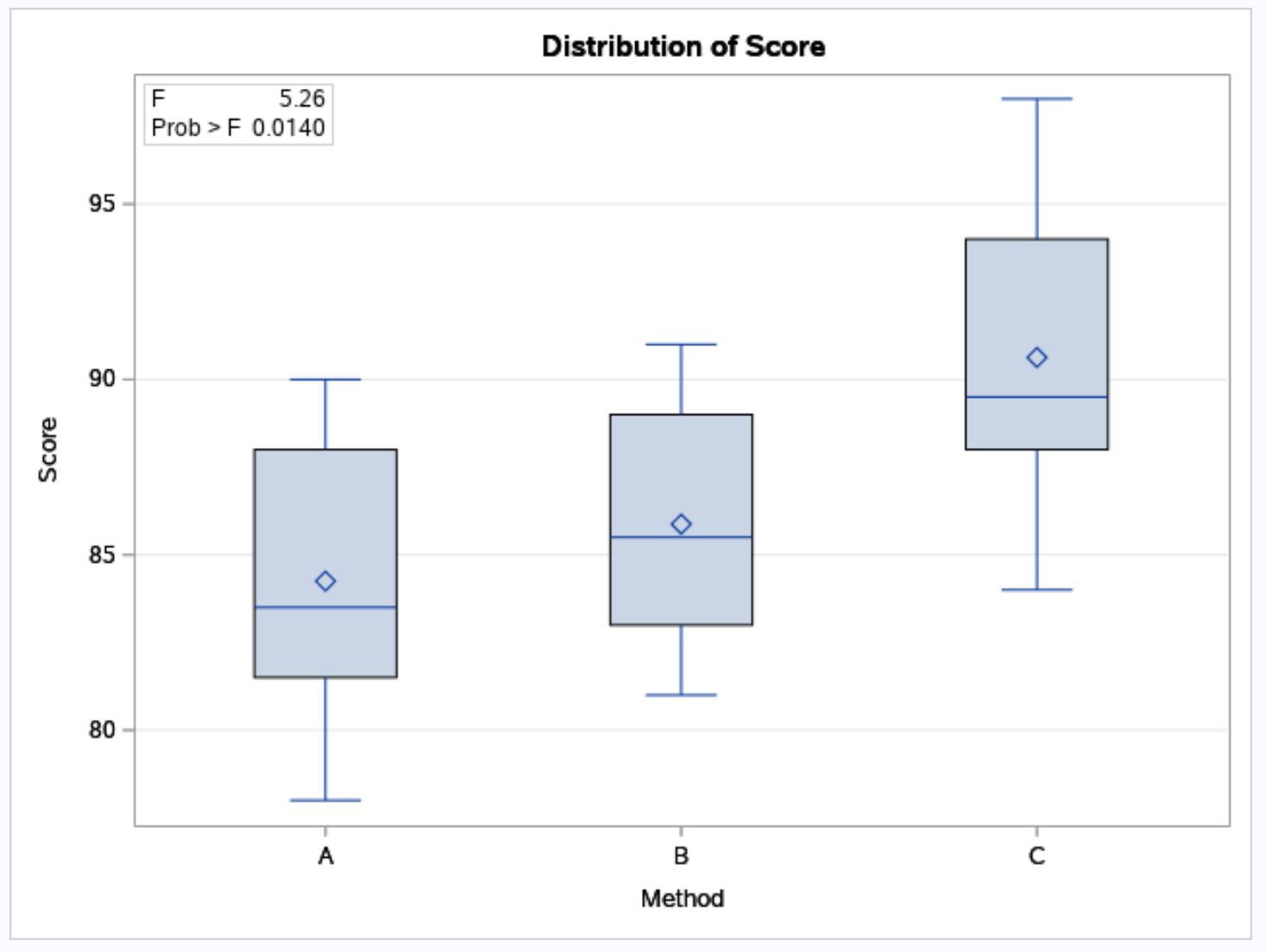
Из диаграмм мы видим, что баллы на экзаменах, как правило, выше среди студентов, которые использовали метод обучения C, по сравнению с методами B и C.

Чтобы точно определить, какие групповые средние значения отличаются, нам нужно обратиться к окончательной таблице результатов, в которой показаны результаты апостериорных тестов Тьюки:

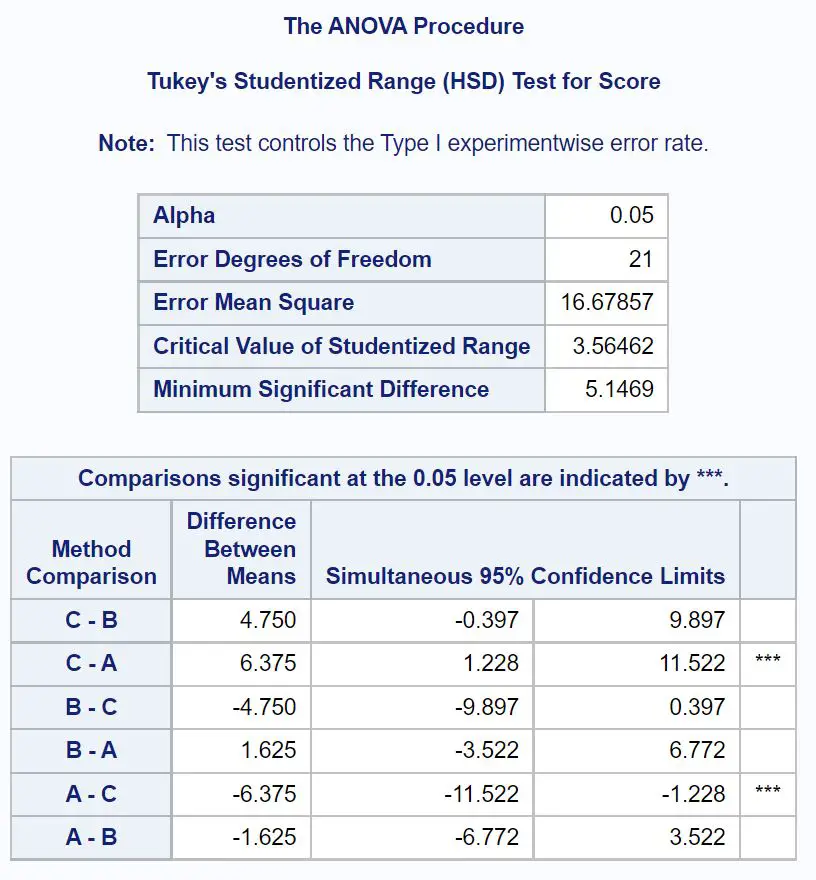
Чтобы выяснить, какие групповые средние значения различаются, нам нужно посмотреть, рядом с какими парными сравнениями стоят звездочки ( *** ).

Из таблицы видно, что средние значения групп А и С статистически значимо различаются.

Мы также можем увидеть 95% доверительный интервал для разницы в средних баллах на экзамене между группами A и C:

95% доверительный интервал для средней разницы: [1,228, 11,522]

Шаг 4. Отчет о результатах

Наконец, мы можем сообщить результаты одностороннего дисперсионного анализа:

Однофакторный дисперсионный анализ был проведен для сравнения влияния трех различных методов исследования на результаты обследования.

Однофакторный дисперсионный анализ показал, что существует статистически значимая разница в среднем балле на экзамене как минимум между двумя группами (F(2,21) = [5,26], p = 0,014).

Тест Тьюки HSD для множественных сравнений показал, что среднее значение экзаменационного балла значительно различалось между методом C и методом A (95% ДИ = [1,228, 11,522]).

Не было статистически значимой разницы в средних баллах на экзамене между методом А и методом Б или между методом Б и методом С.

Дополнительные ресурсы

В следующих руководствах представлена дополнительная информация об однофакторном дисперсионном анализе:

Введение в однофакторный дисперсионный анализ
Односторонний калькулятор ANOVA
Как вручную выполнить однофакторный дисперсионный анализ