Почему медиана важна в статистике?
Медиана представляет собой среднее значение набора данных, когда все значения упорядочены от наименьшего к наибольшему.
Например, медиана в следующем наборе данных равна 19:
Набор данных: 3, 4, 11, 15, 19 , 22, 23, 23, 26.
Медиана также представляет собой 50-й процентиль набора данных. То есть ровно половина значений в наборе данных находится выше медианы, а половина значений — ниже.
Медиана — важная метрика для расчета, поскольку она дает нам представление о том, где находится «центр» набора данных. Это также дает нам представление о «типичном» значении в данном наборе данных.
Например, предположим, что у нас есть набор данных, содержащий цены продажи 10 000 различных домов в определенном городе.

Вместо того, чтобы просматривать ряды необработанных данных , мы можем вычислить медианное значение, чтобы быстро понять среднюю цену продажи домов в этом городе.
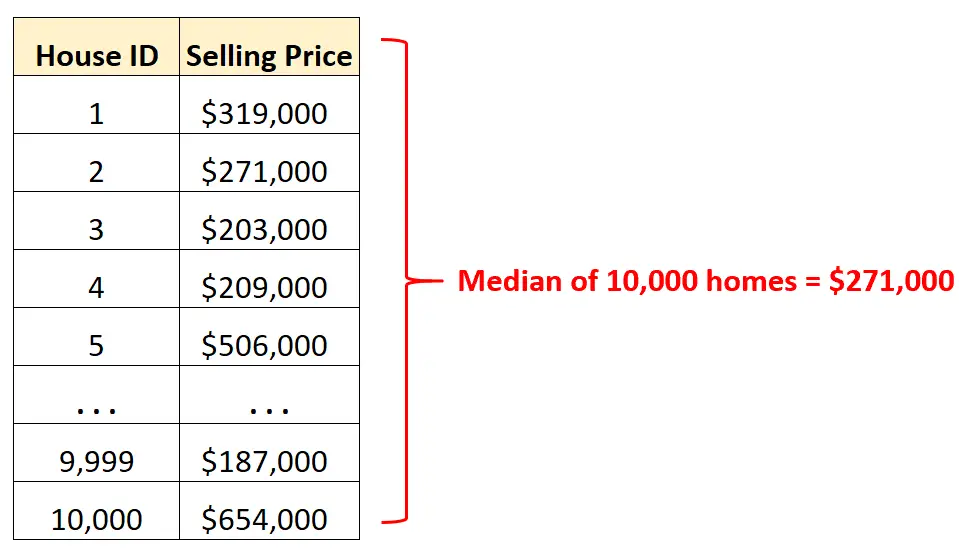
Зная, что средняя цена продажи составляет 271 000 долларов, мы знаем, что ровно половина из 10 000 домов продана дороже этой суммы, а другая половина — дешевле.
Это также дает нам представление о «типичной» цене продажи домов в этом городе.
Когда использовать медиану
Анализируя наборы данных, мы часто хотим понять, в чем заключается центральная ценность.
В статистике есть две распространенные метрики, которые мы используем для измерения центра набора данных:
- Среднее : среднее значение в наборе данных.
- Медиана : медианное значение в наборе данных.
Оказывается, медиана является более полезной мерой в следующих случаях:
- Когда распределение несимметрично .
- Когда распределение содержит выбросы.
Чтобы проиллюстрировать это, рассмотрим следующие два примера.
Пример 1. Вычисление медианы асимметричного распределения
Рассмотрим следующее распределение зарплат жителей определенного города:

Медианное значение лучше отражает «типичную» зарплату жителя, чем среднее значение, поскольку распределение смещено вправо.
Это означает, что высокие заработные платы на правой стороне распределения отодвигают среднее значение от центра распределения.
В этом конкретном примере средняя зарплата составляет 47 000 долларов США, а медианная зарплата — 32 000 долларов США. Медиана гораздо лучше отражает типичную зарплату в этом городе.
Пример 2. Расчет медианы при наличии выбросов
Рассмотрим следующий график, показывающий площадь домов на определенной улице:

На среднее значение сильно влияют несколько чрезвычайно больших домов, а на медиану — нет.
Мы видим, что медиана лучше отражает «типичную» площадь дома на этой улице, чем среднее значение, поскольку на нее не влияют выбросы.
Краткое содержание
Вот краткое изложение основных моментов, затронутых в этой статье:
- Медиана представляет собой среднее значение в наборе данных.
- Медиана важна, потому что она дает нам представление о том, где в наборе данных находится центральное значение.
- Медиана, как правило, более полезна для расчета, чем среднее значение, когда распределение искажено и/или имеет выбросы.
Дополнительные ресурсы
Конкретные примеры: использование среднего значения, медианы и режима
Когда использовать среднее значение или Медиана: с примерами
Почему режим важен в статистике?