Почему режим важен в статистике?
Режим представляет значение, которое чаще всего появляется в наборе данных.
Набор данных может не иметь режимов (если значения не повторяются), иметь один режим или несколько режимов.
Например, режим в следующем наборе данных — 19:
Набор данных: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26.
Это значение, которое встречается чаще всего.
В статистике режим важен по следующим причинам:
Причина 1. Это позволяет нам узнать, какие значения в наборе данных являются наиболее распространенными.
Причина 2. Это полезно для поиска наиболее часто встречающегося значения в категориальных данных, когда невозможно вычислить среднее и медиану.
Причина 3. Это дает нам представление о том, где находится «центр» набора данных, хотя медиана и среднее значение используются чаще (как мы увидим позже в этой статье).
Следующие примеры иллюстрируют каждую из этих причин на практике.
Причина 1. Режим сообщает нам, какое значение встречается чаще всего.
Допустим, у нас есть набор данных из 100 000 строк, содержащий цены продажи домов в США:

Предположим, мы используем статистическое программное обеспечение (например, Excel , R , Python и т. д.) для расчета режима этого набора данных и обнаруживаем, что существует три режима:
- 280 000 долларов США
- 300 000 долларов США
- 305 000 долларов США
Это сразу дает нам представление о наиболее распространенных ценах на жилье в наборе данных.
Вычисление тысяч в режиме также намного быстрее, чем просмотр строк данных и попытка определить, какие цены на жилье встречаются чаще всего.
Причина 2. Режим ищет наиболее распространенное значение в категориальных данных.
Предположим, у нас есть набор данных из 1000 строк, который сообщает нам цвет автомобиля, принадлежащего людям в определенном районе:
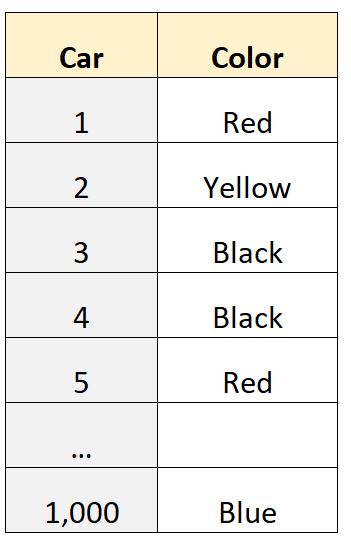
Переменная «цвет» является категориальной переменной , что означает, что значения принадлежат категориям («красный», «желтый», «черный» и т. д.), и поэтому мы не можем вычислить количественное значение, такое как среднее или медианное значение. .
Однако мы можем вычислить режим, поскольку он просто представляет собой наиболее распространенное значение в наборе данных.
Например, мы могли бы использовать статистическое программное обеспечение, чтобы определить, что режим этого набора данных — «черный», что говорит нам о том, что наиболее распространенный цвет автомобиля в этом наборе данных — черный.
Причина 3: Режим дает нам представление о том, где находится центр набора данных.
Режим также считается мерой центральной тенденции , то есть он может дать нам представление о том, где находится «центр» набора данных.
Например, предположим, что у нас есть следующий набор данных, который показывает результаты экзаменов 20 разных учеников в классе:

На модусе получается 82 – это самый распространенный балл на экзамене. Это также является хорошим показателем того, где в этом наборе данных находится «основное» значение оценки по отзывам.
Однако предположим, что вместо этого у нас есть следующий набор данных результатов экзамена:
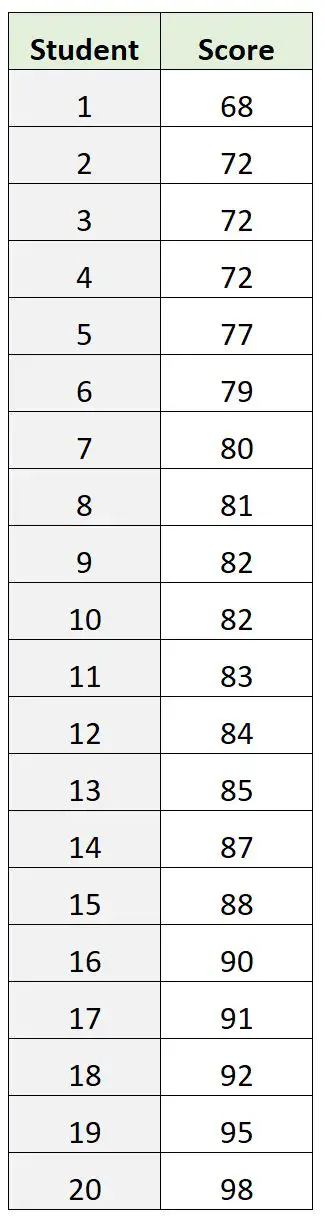
В этом наборе данных 72 — это результат экзамена по моде. Однако это оказывается плохим показателем того, где находится «основной» балл на экзамене.
Средний балл на экзамене составляет 82,9 , а средний балл на экзамене — 82,5 , оба из которых дают нам лучшее представление о том, где находится «центральная» ценность по отношению к моде.
Краткое содержание
Вот краткое изложение основных моментов, затронутых в этой статье:
- Режим представляет значения, которые чаще всего встречаются в наборе данных.
- Этот режим сообщает нам наиболее распространенное значение в категориальных данных, когда нельзя использовать среднее и медиану.
- Режим дает нам представление о том, где находится «центр» набора данных, но он может вводить в заблуждение по сравнению со средним значением или медианой.
Дополнительные ресурсы
Следующие учебные пособия предоставляют дополнительную информацию о среднем значении, медиане и режиме в статистике:
Почему среднее значение важно в статистике?
Почему медиана важна в статистике?
Конкретные примеры: использование среднего значения, медианы и режима
Когда использовать среднее значение или Медиана: с примерами