Взаимовключающие или взаимоисключающие события
Два события являются взаимоисключающими , если они не могут произойти одновременно.
Например, предположим, что событие A — это событие, когда на игральной кости выпадает четное число, а событие B — это событие, когда на игральной кости выпадает нечетное число.
Мы бы определили выборочное пространство для событий следующим образом:
- А = {2, 4, 6}
- Б = {1, 3, 5}
Обратите внимание, что между двумя выборочными пространствами нет перекрытия. Таким образом, события A и B являются взаимоисключающими, поскольку они не могут произойти одновременно. Число, на которое выпадает игральная кость, не может быть одновременно четным и нечетным.
И наоборот, два события являются взаимовключающими , если они могут произойти одновременно.
Например, пусть событие C — это событие, когда на кубике выпадает четное число, а событие D — событие, когда на кубике выпадает число больше 3.
Мы бы определили выборочное пространство для событий следующим образом:
- С = {2, 4, 6}
- д = {4, 5, 6}
Обратите внимание, что между двумя выборочными пространствами существует перекрытие. Таким образом, события C и D являются взаимовключающими, поскольку могут произойти одновременно. Вполне возможно, что на кубике выпадет четное число больше 3.
Вероятности событий
Если два события являются взаимоисключающими , то вероятность того, что они оба произойдут, равна нулю.
Например, рассмотрим два примера пространства для событий A и B выше:
- А = {2, 4, 6}
- Б = {1, 3, 5}
Поскольку выборочные пространства не перекрываются, мы бы сказали, что P(A и B) = 0 .
Но если два события являются взаимовключающими , то вероятность того, что они оба произойдут, будет числом, большим нуля.
Например, рассмотрим ранее два примера пространства для событий C и D:
- С = {2, 4, 6}
- д = {4, 5, 6}
Поскольку существует 6 возможных чисел, на которые может выпасть игральная кость, и два из этих чисел (4 и 6) принадлежат как событиям C, так и D, мы бы вычислили P(C и D) как 2/6 или 1/3 .
Просмотр взаимовключающих и взаимоисключающих событий
Мы часто используем диаграммы Венна для визуализации вероятностей, связанных с событиями.
Если два события являются взаимоисключающими , они вообще не будут перекрываться на диаграмме Венна:
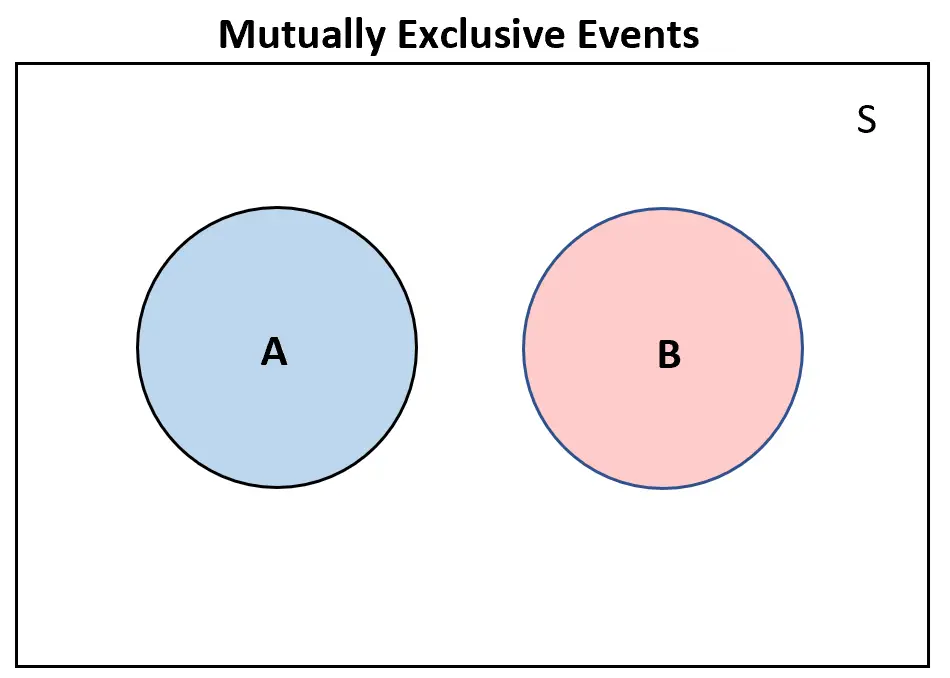
И наоборот, если два события являются взаимовключающими , на диаграмме Венна будет хотя бы некоторое перекрытие:
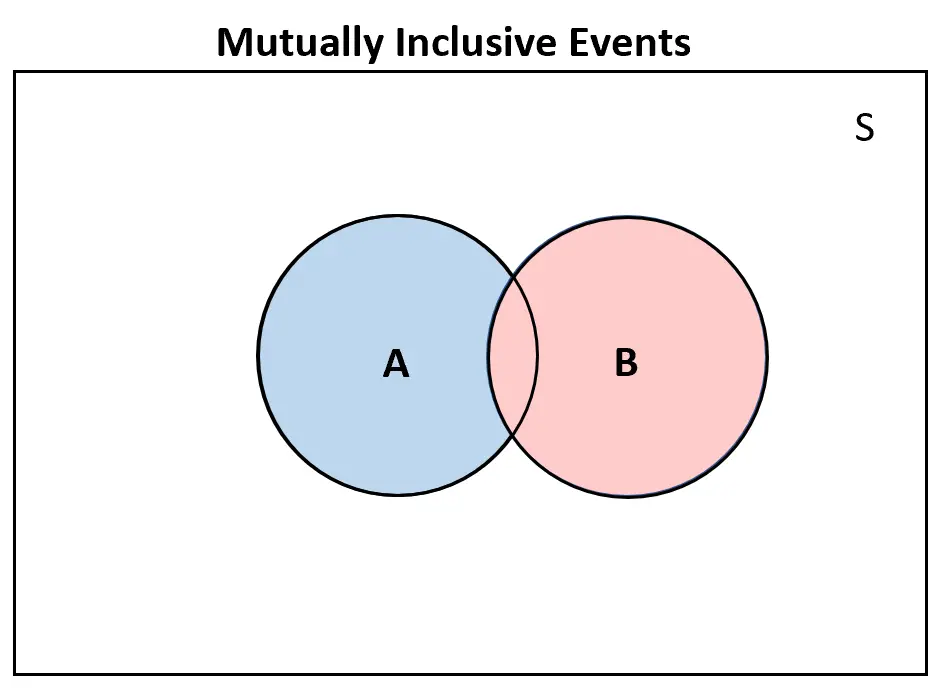
Дополнительные ресурсы
Введение в теоретическую вероятность
Общее правило умножения
Что такое непересекающиеся события?