Как выполнить взвешенную регрессию наименьших квадратов в r

Одним из ключевых предположений линейной регрессии является то, что остатки распределяются с одинаковой дисперсией на каждом уровне переменной-предиктора. Это предположение известно как гомоскедастичность .

Если это предположение не соблюдается, говорят, что в остатках присутствует гетероскедастичность . Когда это происходит, результаты регрессии становятся ненадежными.

Одним из способов решения этой проблемы является использование взвешенной регрессии наименьших квадратов , которая присваивает веса наблюдениям таким образом, что наблюдения с низкой дисперсией ошибок получают больший вес, поскольку они содержат больше информации по сравнению с наблюдениями с большей дисперсией ошибок.

В этом руководстве представлен пошаговый пример выполнения регрессии взвешенных наименьших квадратов в R.

Шаг 1. Создайте данные

Следующий код создает фрейм данных, содержащий количество изученных часов и соответствующий результат экзамена для 16 студентов:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Шаг 2. Выполните линейную регрессию

Далее мы воспользуемся функцией lm() , чтобы подогнать простую модель линейной регрессии , которая использует часы в качестве предикторной переменной и оценку в качестве переменной отклика :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Шаг 3. Проверка гетероскедастичности

Далее мы создадим график остатков и подогнанных значений для визуальной проверки гетероскедастичности:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

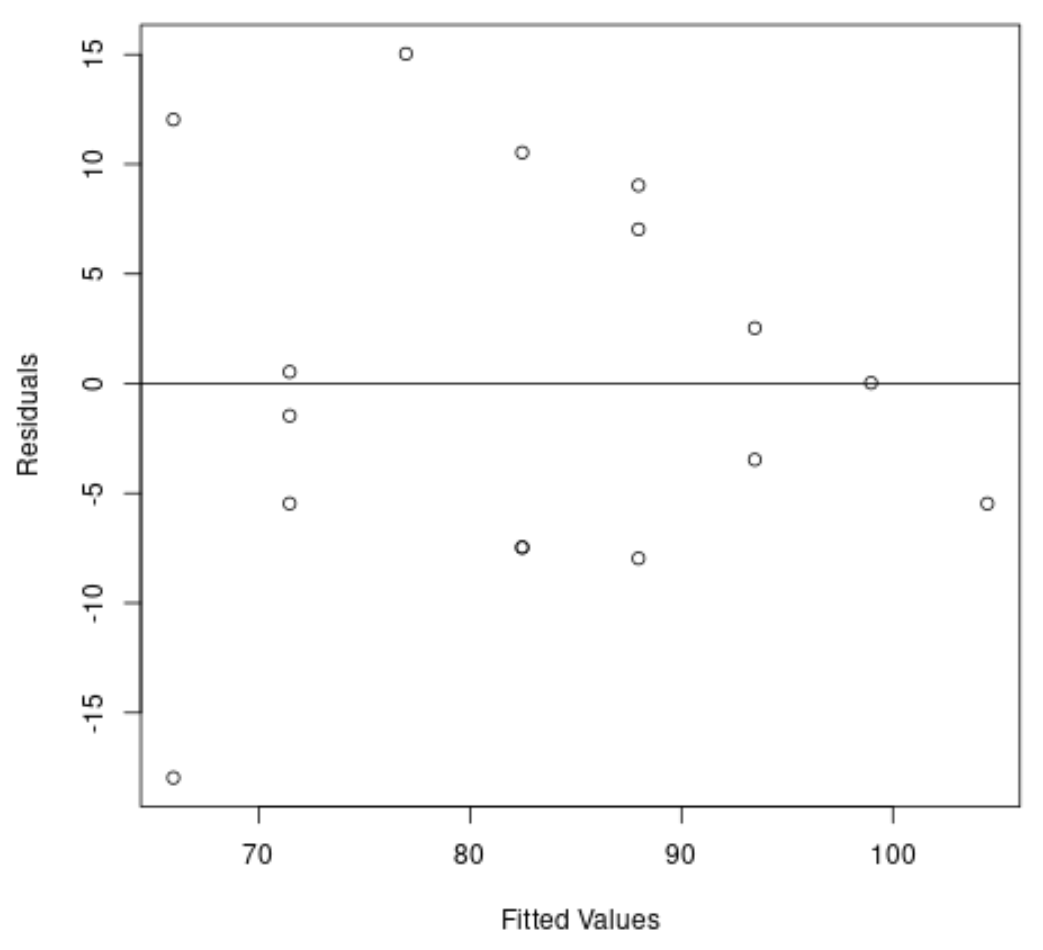
Из графика видно, что остатки имеют форму «конуса»: они не распределены с одинаковой дисперсией по всему графику.

Чтобы формально проверить гетероскедастичность, мы можем выполнить тест Бреуша-Пэгана:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Тест Бреуша-Пэгана использует следующие нулевые и альтернативные гипотезы :

• Нулевая гипотеза (H ₀ ): гомоскедастичность присутствует (остатки распределяются с равной дисперсией)
• Альтернативная гипотеза ( _HA ): присутствует гетероскедастичность (остатки не распределяются с одинаковой дисперсией)

Поскольку значение p теста составляет 0,0466 , мы отвергнем нулевую гипотезу и придем к выводу, что гетероскедастичность является проблемой в этой модели.

Шаг 4. Выполните взвешенную регрессию наименьших квадратов.

Поскольку присутствует гетероскедастичность, мы выполним взвешенный метод наименьших квадратов, установив веса так, чтобы наблюдения с более низкой дисперсией получали больший вес:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

Из результатов мы видим, что оценка коэффициента для переменной-предиктора часов немного изменилась, и общее соответствие модели улучшилось.

Модель взвешенных наименьших квадратов имеет остаточную стандартную ошибку 1,199 по сравнению с 9,224 в исходной модели простой линейной регрессии.

Это указывает на то, что прогнозируемые значения, полученные с помощью модели взвешенных наименьших квадратов, намного ближе к фактическим наблюдениям по сравнению с прогнозируемыми значениями, полученными с помощью простой модели линейной регрессии.

Модель взвешенных наименьших квадратов также имеет R-квадрат 0,6762 по сравнению с 0,6296 в исходной простой модели линейной регрессии.

Это указывает на то, что модель взвешенных наименьших квадратов способна объяснить большую дисперсию оценок на экзамене, чем простая модель линейной регрессии.

Эти измерения показывают, что модель взвешенных наименьших квадратов обеспечивает лучшее соответствие данным по сравнению с простой моделью линейной регрессии.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить квантильную регрессию в R