Средние типы (статистика)

К бенджамин андерсон 6 августа, 2023 Статистика 0 комментариев

Здесь мы объясним, что такое все типы средних значений в статистике и как они рассчитываются. Вы найдете формулы для каждого типа чулок и примеры.

Но прежде чем увидеть, какие бывают типы средних значений, мы должны логически понять, что такое среднее значение в статистике. Поэтому мы рекомендуем вам просмотреть следующую ссылку, прежде чем продолжить.

➤ См.: Что такое средний показатель (статистика)?

Какие бывают средние значения в статистике?

В статистике различают следующие виды средних значений:

Среднее арифметическое
Средневзвешенное
Геометрические средства
корень означает квадрат
гармонический смысл
обобщенное среднее
обобщенное f-среднее
обрезанные средства
межквартильное среднее
среднее значение функции

Далее мы объясним, как рассчитывать все типы средних значений в статистике. Пять наиболее часто используемых типов среднего — это среднее арифметическое, средневзвешенное, среднее геометрическое, среднее квадратичное и среднее гармоническое. Итак, мы собираемся более подробно рассказать об этих пяти основных типах средств массовой информации.

Среднее арифметическое

Среднее арифметическое рассчитывается путем сложения всех значений и последующего деления на общее количество точек данных.

Таким образом, формула среднего арифметического выглядит следующим образом:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

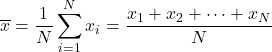
Среднее арифметическое также известно как среднее арифметическое .

Среднее арифметическое, вероятно, является наиболее используемым типом среднего в статистике.

Чтобы увидеть пример того, как получается среднее значение этого типа, мы рассчитаем среднее арифметическое следующих данных:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Чтобы вычислить среднее арифметическое, просто сложите все статистические данные и разделите на общее количество данных, равное 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Средневзвешенное

Чтобы вычислить средневзвешенное значение, необходимо сначала умножить каждые статистические данные на их вес (или вес), затем сложить все продукты и, наконец, разделить взвешенную сумму на сумму всех весов.

Таким образом, формула средневзвешенного значения выглядит следующим образом:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

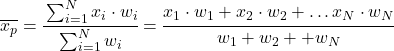
Где x _i — статистическое значение, а w _{i —} его соответствующий вес.

Средневзвешенное значение сложнее понять, поэтому мы рекомендуем просмотреть следующий пример, который шаг за шагом объясняет, как оно рассчитывается:

➤ См.: Пример средневзвешенного значения.

Геометрические средства

Среднее геометрическое набора статистических данных равно корню n-й степени из произведения всех значений.

Этот тип среднего используется в бизнес-финансах для расчета нормы прибыли, средних процентных значений и сложных процентов.

Формула этого типа хранения довольно сложна. Фактически, среднее геометрическое всех статистических наборов невозможно вычислить, но иногда этот тип среднего значения не может быть определен. Вот почему мы рекомендуем вам ознакомиться со всеми исключениями, описанными по следующей ссылке:

➤ См.: формула среднего геометрического.

корень означает квадрат

Среднеквадратичное значение равно квадратному корню из среднего арифметического квадратов данных.

Таким образом, формула среднеквадратического значения выглядит следующим образом:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Этот тип среднего значения также называется среднеквадратичным , среднеквадратичным или RMS .

Отметим лишь, что среднее кубическое тоже существует, но используется в весьма особых случаях.

Усреднение квадратов имеет свои преимущества и недостатки, например, оно особенно полезно, когда статистическая переменная принимает положительные и отрицательные значения, поскольку при возведении в квадрат каждого фрагмента данных все значения становятся положительными. Вы можете увидеть больше возможностей этого типа носителя, нажав следующую ссылку:

➤ См.: преимущества и недостатки среднеквадратического метода.

гармонический смысл

Среднее гармоническое рассчитывается путем деления общего количества статистических данных на сумму обратных величин каждого значения.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

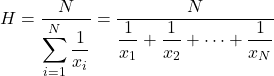
Среднее гармоническое значение используется для расчета средних скоростей, времени или проведения электронных расчетов. Эта характеристика отличает гармоническое среднее от других типов средних, часто используемых при расчете средних цен или процентов.

Примеры расчета этого типа среднего вы можете увидеть на следующей странице:

➤ См.: примеры гармонического значения.

Другие виды чулок

В этом разделе мы увидим формулы для других видов чулок. Мы не будем подробно останавливаться на каждом типе, поскольку они не получили широкого распространения, но вам будет полезно знать, что существуют и другие типы чулок.

Обобщенное среднее представляет собой смесь типов средних, рассмотренных выше, и рассчитывается по следующей формуле:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

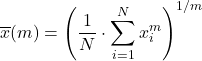
Пусть f — инъективная и монотонная функция, тогда обобщенное f-среднее определяется как:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

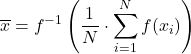
Обрезанное среднее предполагает вычисление среднего арифметического после вычитания процента наблюдений в верхнем и нижнем концах выборки. Один и тот же процент должен быть отклонен на обоих концах.

Для расчета интерквартильного среднего , также называемого интерквартильным средним, данные первого и четвертого квартилей сначала отбрасываются, а затем вычисляется только среднее арифметическое второго и третьего квартилей выборки. Таким образом, формула для этого типа среднего выглядит так:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

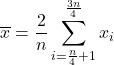
Наконец, вы также можете найти среднее значение функции . Среднее значение непрерывной функции на отрезке [a,b] рассчитывается по следующей формуле:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Выборка и среднее по совокупности

Наконец, мы увидим, в чем разница между средним показателем по выборке и средним по совокупности — двумя типами средних значений, которые часто путают.

Среднее значение выборки — это среднее значение, рассчитанное по значениям статистической выборки, то есть оно рассчитывается по части всех значений переменной.

Среднее по численности населения — это среднее значение, рассчитанное по статистической совокупности, то есть по всем значениям переменной. Следовательно, среднее значение генеральной совокупности совпадает с математическим ожиданием переменной.

Выборочное среднее можно считать практически равным генеральному среднему, если известен достаточно большой объем данных. Но значение генеральной совокупности получить очень сложно, поскольку в действительности все значения распределения редко известны.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше