Вот как найти значение p из таблицы распределения f.
Таблица распределения F представляет собой таблицу, в которой показаны критические значения распределения F. Чтобы использовать таблицу распределения F, вам нужны всего три значения:
- Степени свободы числителя
- Степени свободы знаменателя
- Альфа-уровень
Распределение F чаще всего используется в дисперсионном анализе или сокращенно ANOVA . Например, вот как может выглядеть таблица результатов ANOVA:
| Источник | SS | дф | РС. | Ф | П. |
|---|---|---|---|---|---|
| Уход | 58,8 | 2 | 29,4 | 1,74 | 0,217 |
| Ошибка | 202,8 | 12 | 16,9 | ||
| Общий | 261,6 | 14 |
В этом примере степени свободы в числителе статистики F равны 2 , степени свободы в знаменателе статистики F равны 12 , а сама статистика F равна 1,74 . Предположим, что используемый нами альфа-уровень равен 0,10. В таблице выше мы видим, что значение p для этой статистики F составляет 0,217. Поскольку 0,217 выше уровня альфа, мы пришли к выводу, что эта статистика F не является статистически значимой.
Если бы мы хотели вместо этого использовать таблицу распределения F , мы бы использовали таблицу распределения F для альфа = 0,10. Мы бы нашли в таблице критическое значение, которое соответствует степени свободы в числителе 2 (DF1 = 2 в таблице) и степени свободы в знаменателе 12 (DF2 = 12 в таблице) и отметили бы что это значение равно 2,8068. .

Поскольку наша статистика F 1,74 из таблицы ANOVA не превышает критического значения F 2,8068 из таблицы распределения F, мы пришли бы к выводу, что статистика F не является значимой на уровне альфа 0,10.
Таблица распределения F предоставляет критические значения, а не значения P.
Обратите внимание, что в приведенном выше примере таблица распределения F просто дает нам критическое значение F для сравнения нашей статистики F. Таблица распределения F не дает нам напрямую значения ap.
Если у вас есть статистика F со степенями свободы в числителе и степенями свободы в знаменателе, и вы хотите найти соответствующее значение p, вам нужно будет использовать калькулятор распределения F.
Например, предположим, что мы знаем, что наша статистика F равна 1,74, степени свободы в числителе равны 2, а степени свободы в знаменателе равны 12, и мы хотим найти значение p для этой статистики F. В этом случае мы должны ввести следующие числа в калькулятор распределения F:
Примечание. Оставьте последнее поле пустым. Калькулятор автоматически найдет для вас это значение.
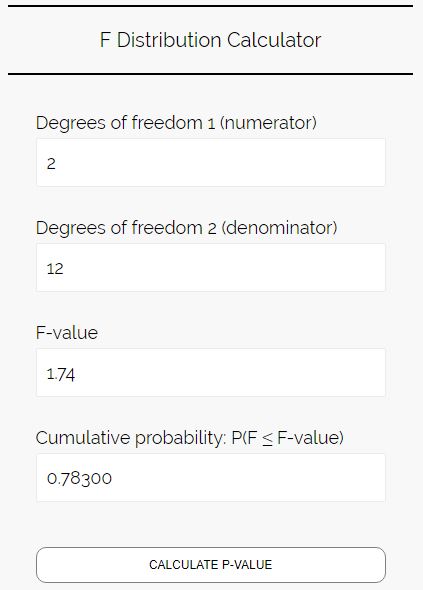
Это говорит нам о том, что совокупная вероятность равна 0,78300. Это область слева от статистики F в распределении F. Обычно нас интересует область справа от статистики F, поэтому в этом случае значение p будет равно 1 – 0,78300 = 0,217.
Когда использовать таблицу распределения F
Если вы хотите найти критическое значение F для заданных степеней свободы числителя, степеней свободы знаменателя и альфа-уровня, вам необходимо использовать таблицу распределения F.
Вместо этого, если у вас есть заданная статистика F (из ANOVA или другого статистического теста) с заданными степенями свободы числителя и знаменателя и вы просто хотите узнать значение p этой статистики F, тогда вам нужно будет использовать Калькулятор распределения F для этого.