Выборочное распределение

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое выборочное распределение в статистике и для чего оно используется. Так вы найдете значение выборочного распределения, конкретный пример выборочного распределения и, кроме того, формулы для наиболее распространенных типов выборочных распределений.

Каково распределение выборки?

Распределение выборки или распределение выборки — это распределение, которое получается в результате рассмотрения всех возможных выборок из совокупности. Другими словами, распределение выборки — это распределение, полученное путем расчета параметра выборки всех возможных выборок из совокупности.

Например, если мы извлекаем все возможные выборки из статистической совокупности и вычисляем среднее значение каждой выборки, набор выборочных средних образует выборочное распределение. Точнее, поскольку вычисляемый параметр является средним арифметическим, то это выборочное распределение среднего.

В статистике выборочное распределение используется для расчета вероятности приближения к значению параметра генеральной совокупности при изучении одной выборки. Аналогичным образом распределение выборки позволяет нам оценить ошибку выборки для заданного размера выборки.

Пример распределения выборки

Теперь, когда мы знаем определение выборочного распределения, давайте рассмотрим простой пример, чтобы полностью понять эту концепцию.

В коробку мы кладем три шара, и на каждом из них записано число от одного до трех, так что один шар имеет номер 1, другой шар имеет номер 2, а последний шар имеет номер 3. Для выборки размера n = 2, вычисляет вероятности выборочного распределения среднего значения, если выбраны выборки с заменой.

Выборка проб осуществляется с заменой, то есть шарик, подобранный для выбора первого элемента выборки, возвращается в коробку и может быть выбран снова при втором извлечении. Таким образом, все возможные выборки из совокупности:

1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3

Таким образом, вычисляем среднее арифметическое каждой возможной выборки:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Следовательно, вероятности получения каждого значения выборочного среднего при отборе случайной выборки из совокупности следующие:

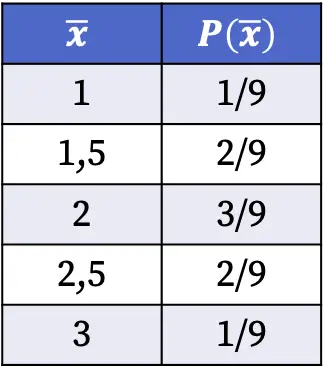
Вероятности распределения выборок, показанные в таблице выше, были рассчитаны путем деления количества образцов, имеющих указанное среднее значение, на общее количество возможных случаев. Например: выборочное среднее равно 1,5 в двух случаях из девяти возможных, следовательно, P(1,5)=2/9.

Типы выборочных распределений

Распределения выборки (или распределения выборки) можно классифицировать на основе параметра выборки, из которого они были получены. Итак, наиболее распространенными видами раздач являются следующие:

Выборочное распределение среднего значения : это выборочное распределение, которое получается в результате вычисления среднего арифметического каждой выборки.
Пропорциональное распределение выборки : это распределение выборки, полученное путем расчета доли всех образцов.
Выборочное распределение дисперсии : это выборочное распределение, которое формирует набор всех дисперсий в выборке.
Разница средних значений выборочного распределения : это выборочное распределение, которое получается в результате расчета разницы между средними значениями всех возможных выборок из двух разных групп населения.
Разница в пропорциях Распределение выборки : это распределение выборки, полученное путем вычитания всех возможных пропорций выборки из двух совокупностей.

Каждый тип распределения выборки объясняется более подробно ниже.

Выборочное распределение среднего значения

Учитывая популяцию, которая следует нормальному распределению вероятностей со средним значением

$\mu$

и стандартное отклонение

$\sigma$

и образцы размеров извлекаются

$n$

, выборочное распределение среднего значения также будет определяться нормальным распределением, имеющим следующие характеристики:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Золото

$\mu_{\overline{x}}$

является средним значением выборочного распределения среднего и

$\sigma_{\overline{x}}$

это его стандартное отклонение. Более того,

$\cfrac{\sigma}{\sqrt{n}}$

— стандартная ошибка выборочного распределения.

Примечание. Если генеральная совокупность не соответствует нормальному распределению, но размер выборки велик (n>30), выборочное распределение среднего значения также можно аппроксимировать к нормальному распределению, указанному выше, с помощью предела центральной теоремы.

Следовательно, поскольку выборочное распределение среднего значения соответствует нормальному распределению, формула для расчета любой вероятности, связанной с выборочным средним, выглядит следующим образом:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Золото:

$\overline{x}$

это образец означает.
$\mu$

Это средний показатель по численности населения.
$s$

— стандартное отклонение генеральной совокупности.
$n$

это размер выборки.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

➤ См.: Решенное упражнение по выборочному распределению среднего значения.

Выборочное распределение доли

Фактически, когда мы изучаем часть выборки, мы анализируем случаи успеха. Таким образом, случайная величина в исследовании имеет биномиальное распределение вероятностей.

Согласно центральной предельной теореме, для больших размеров (n>30) мы можем приблизить биномиальное распределение к нормальному. Таким образом, выборочное распределение доли приближается к нормальному распределению со следующими параметрами:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Золото

$p$

это вероятность успеха и

$q$

это вероятность неудачи

$q=1-p$

Примечание. Биномиальное распределение можно приблизить к нормальному распределению только в том случае, если

$n>30″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»52″ style=»vertical-align: -2px;»></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Следовательно, поскольку выборочное распределение доли можно приблизить к нормальному распределению, формула для расчета любой вероятности, связанной с долей выборки, имеет следующий вид:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Золото:

$\widehat{p}$

– это доля выборки.
$p$

это доля населения.
$q$

— вероятность отказа популяции,

$q=1-p$

.
$n$

это размер выборки.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

➤ См.: Решенное упражнение по выборочному распределению доли

Выборочное распределение дисперсии

Выборочное распределение дисперсии определяется распределением вероятностей хи-квадрат. Следовательно, формула статистики выборочного распределения дисперсии имеет вид:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Золото:

$\chi^2$

— это статистика выборочного распределения дисперсии, которая соответствует распределению хи-квадрат.
$n$

это размер выборки.
$s^2$

— выборочная дисперсия.
$\sigma^2$

это популяционная дисперсия.

➤ См.: Решенное упражнение по выборочному распределению дисперсии.

Выборочное распределение разницы средних

Если размер выборки достаточно велик (n ₁ ≥30 и n ₂ ≥30), выборочное распределение средней разницы соответствует нормальному распределению. Точнее, параметры указанного распределения рассчитываются следующим образом:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Примечание. Если обе совокупности имеют нормальное распределение, то выборочное распределение разницы средних значений следует нормальному распределению независимо от размеров выборки.

Следовательно, поскольку выборочное распределение разницы средних значений определяется нормальным распределением, формула для расчета статистики выборочного распределения разницы средних значений имеет вид:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Золото:

$\overline{x_i}$

является средним значением выборки i.
$\mu_i$

является средним значением численности населения i.
$\sigma_i$

— стандартное отклонение генеральной совокупности i.
$n_i$

размер выборки i.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

Обратите внимание, что выборки из разных групп населения могут иметь разные размеры выборки.

➤ См.: Решенное упражнение по выборочному распределению разницы средних значений.

Выборочное распределение разницы в пропорциях

Выборки, отобранные по разнице в пропорциях выборочного распределения, определяются биномиальными распределениями, поскольку для практических целей пропорция представляет собой отношение успешных случаев к общему числу наблюдений.

Однако благодаря центральной предельной теореме биномиальные распределения можно аппроксимировать к нормальным распределениям вероятностей. Следовательно, выборочное распределение разницы в пропорциях можно приблизить к нормальному распределению со следующими характеристиками:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Примечание. Выборочное распределение разницы в пропорциях можно приблизить к нормальному распределению только в том случае, если

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Следовательно, поскольку выборочное распределение разницы долей можно приблизить к нормальному распределению, формула расчета статистики выборочного распределения разницы долей имеет следующий вид:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Золото:

$\widehat{p_i}$

– это выборочная доля i.
$p_i$

представляет собой долю населения i.
$q_i$

— вероятность отказа популяции i,

$q_i=1-p_i$

.
$n_i$

размер выборки i.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

➤ См.: Решенное упражнение на выборочное распределение разницы долей.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Каково распределение выборки?

Пример распределения выборки

Типы выборочных распределений

Выборочное распределение среднего значения

Выборочное распределение доли

Выборочное распределение дисперсии

Выборочное распределение разницы средних

Выборочное распределение разницы в пропорциях

Об авторе

бенджамин андерсон

Добавить комментарий