Умозаключение и предсказание: в чем разница?

Часто в статистике мы хотим использовать данные по одной из двух причин:

(1) Вывод: мы хотим понять природу взаимосвязи между переменными-предикторами и переменной ответа в существующем наборе данных.

(2) Прогноз: мы хотим использовать существующий набор данных для построения модели, которая прогнозирует значение переменной ответа нового наблюдения.

Например, предположим, что у нас есть следующий набор данных, содержащий информацию о домах:

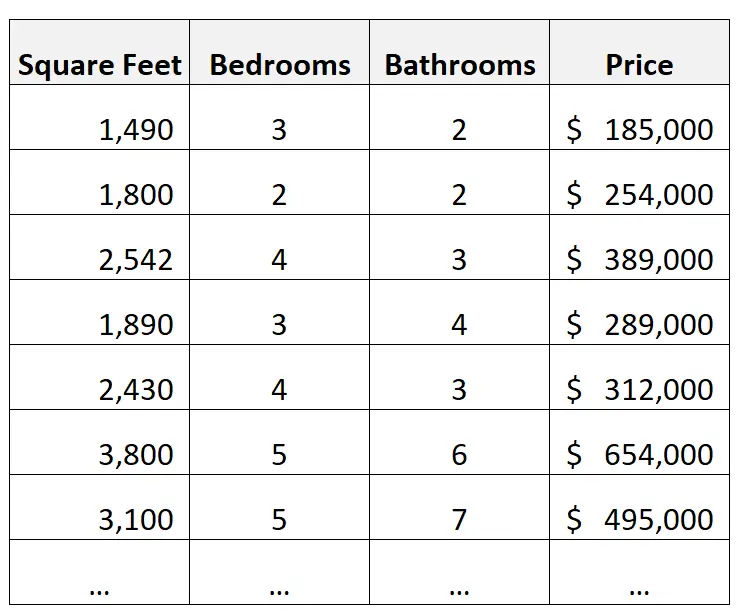
Пример вывода:

Предположим, мы создаем модель множественной линейной регрессии, используя площадь в квадратных футах, количество спален и количество ванных комнат в качестве предикторных переменных, а цену в качестве переменной ответа.

Затем мы могли бы использовать коэффициенты регрессии, чтобы понять среднее изменение цены, связанное с изменением на одну единицу каждой из переменных-предсказателей.

Например, мы могли бы понять, насколько меняется цена (в среднем) с каждой дополнительной спальней, каждой дополнительной ванной комнатой и каждым дополнительным квадратным футом.

Пример прогноза:

Мы могли бы построить ту же модель множественной линейной регрессии и использовать ее для прогнозирования стоимости нового дома на основе его площади, количества спален и ванных комнат.

Например, мы могли бы использовать эту модель для прогнозирования цены нового дома с 3 спальнями, 3 ванными комнатами и площадью 2000 квадратных футов.

Затем мы могли бы сравнить наш прогноз с фактической ценой листинга и оценить, является ли дом недооцененным или переоцененным.

Следующие примеры иллюстрируют разницу между выводом и прогнозированием в разных сценариях:

Пример 1: Выводы и прогнозы в спорте

Предположим, у нас есть следующий набор данных, содержащий информацию о профессиональных баскетбольных командах:

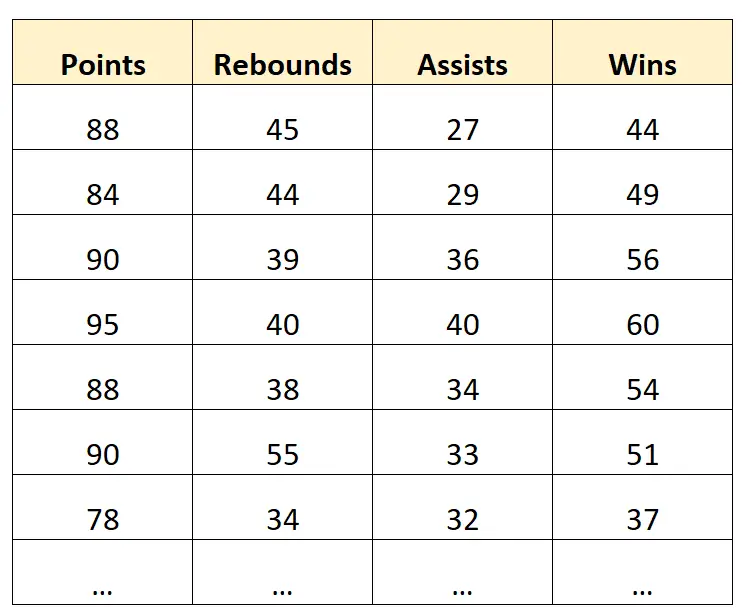
Пример вывода:

Предположим, мы создаем модель множественной линейной регрессии, используя очки, подборы и передачи в качестве переменных-предсказателей, а победы в качестве переменной ответа.

Затем мы могли бы использовать модель, чтобы понять, насколько меняется количество побед (в среднем) с каждым дополнительным очком, подбором и передачей.

Пример прогноза:

Мы могли бы построить ту же модель множественной линейной регрессии и использовать ее для прогнозирования количества побед команды на основе количества очков, подборов и передач.

Например, мы могли бы использовать модель, чтобы предсказать, сколько побед будет у команды с 90 очками, 40 подборами и 30 передачами.

Пример 2: Выводы и прогнозы в бизнесе

Предположим, у нас есть следующий набор данных, содержащий информацию о годовой выручке (в миллионах) различных компаний:

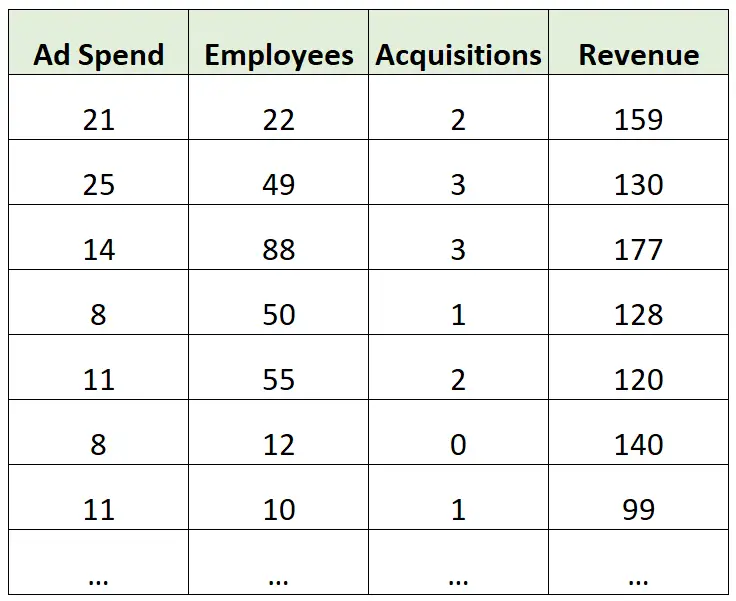
Пример вывода:

Предположим, мы создаем модель множественной линейной регрессии, используя расходы на рекламу, количество сотрудников и общее количество приобретений в качестве переменных-предсказателей, а годовой доход в качестве переменной ответа.

Затем мы могли бы использовать модель, чтобы понять, насколько меняется общий годовой доход (в среднем) с каждым дополнительным долларом, потраченным на рекламу, каждым дополнительным сотрудником и каждым дополнительным приобретением.

Пример прогноза:

Мы могли бы построить ту же модель множественной линейной регрессии и использовать ее для прогнозирования годового дохода компании на основе ее общих маркетинговых расходов, количества сотрудников и общего объема приобретений.

Например, мы могли бы использовать эту модель для прогнозирования годового дохода компании, которая тратит 25 миллионов долларов на рекламу, имеет 40 сотрудников и совершила 2 приобретения.

Дополнительные ресурсы

В следующих руководствах представлена дополнительная информация о важных для понимания терминах статистики:

Описательная или инференциальная статистика: в чем разница?
Уровни измерения: номинальный, порядковый, интервальный и коэффициентный.
Качественные и количественные переменные: в чем разница?