Гармоническое среднее

Здесь мы объясним, что такое среднее гармоническое и как оно рассчитывается (формула). Кроме того, мы шаг за шагом вычисляем среднее гармоническое значение примера. Вы также найдете калькулятор, позволяющий рассчитать среднее гармоническое значение любого набора данных. И, наконец, вы сможете увидеть, каковы свойства среднего гармонического значения.

Что такое гармоническое среднее?

Среднее гармоническое является центральной мерой описательной статистики. Среднее гармоническое рассчитывается путем деления общего количества статистических данных на сумму обратных величин каждого значения.

Среднее гармоническое значение используется для расчета средних скоростей, времени или проведения электронных расчетов. Эта особенность отличает гармоническое среднее от других типов средних, часто используемых при расчете средних цен или процентов.

Итак, формула среднего гармонического значения выглядит следующим образом:

Среднее гармоническое обычно обозначается заглавной буквой H.

Другими существующими типами средних являются среднее арифметическое, средневзвешенное, среднее квадратичное и среднее геометрическое. Гармоническое среднее имеет преимущества и недостатки по сравнению с другими видами среднего, ниже мы увидим, какие они есть.

Как рассчитать среднее гармоническое

Для расчета среднего гармонического значения необходимо выполнить следующие шаги:

1. Рассчитайте обратную величину каждого статистического показателя в выборке.
2. Добавьте все рассчитанные обратные значения.
3. Разделите общее количество данных на сумму, найденную на предыдущем шаге.
4. Полученный результат представляет собой среднее гармоническое статистической выборки.

👉 Как видите, получение среднего гармонического набора данных требует большого количества операций, поэтому делать это вручную довольно трудоемко. Поэтому для расчета среднего гармонического значения мы рекомендуем воспользоваться калькулятором, представленным ниже.

Пример гармонического среднего значения

Познакомившись с теорией среднего гармонического значения, мы увидим, как найти среднее гармоническое набора данных, решив пошаговый пример цены акции.

• Человек покупает акции компании каждый год в течение 5 лет подряд. В течение этого периода цена акций сильно колебалась: в первый год каждая акция стоила 7 евро, во второй год 10 евро, в третий год 15 евро, в четвертый год компания понесла значительные финансовые потери, а цена упала до 6 евро за акцию, и в конце концов, на пятый год компания сделала крупную инвестицию, которая подняла цену до 11 евро. Какова была средняя цена покупки акций?

Один из вариантов — рассчитать среднее арифметическое, то есть сложить все цены и разделить их на пять. Однако, поскольку закупки совершались в разные годы, брать среднее арифметическое было бы ошибкой. Поэтому мы должны найти гармоническое среднее всех цен.

Далее мы применяем формулу среднего гармонического значения:

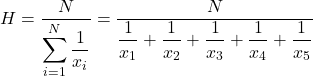
А затем подставляем проблемные значения цен в формулу и вычисляем среднее гармоническое:

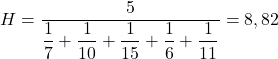
Вам нужно поставить пять в числителе дроби, потому что существует пять разных частей информации.

Таким образом, средняя цена акций, купленных вами в этот период, составляет 8,82 евро за акцию.

Калькулятор среднего гармонического значения

С помощью следующего калькулятора вы можете рассчитать среднее гармоническое значение любого набора статистических данных.

Вы должны вводить числа, используя точку в качестве десятичного разделителя и разделяя числа пробелом. Помните, что для нахождения среднего гармонического значения ни одно значение не может быть нулевым.

Свойства среднего гармонического значения

Гармоническое среднее имеет следующие характеристики:

• Большие значения мало влияют на среднее гармоническое ансамбля, то есть очень большое значение относительно других данных не вызовет заметного изменения среднего гармонического.

• С другой стороны, небольшое значение сильно влияет на среднее гармоническое значение ансамбля, значительно снижая его ценность. Действительно, тогда обратные знаменателю формулы принимают очень большие значения.

• Среднее гармоническое невозможно вычислить, если какие-либо данные равны нулю, поскольку это приведет к неопределенности в формуле. В таком случае среднее гармоническое называется неопределенным.

• Обратная величина гармонического среднего эквивалентна среднему арифметическому обратных величин наблюдений.

• Для той же группы данных среднее гармоническое будет меньше или равно среднему арифметическому.

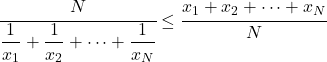
Рассчитать среднее гармоническое с помощью Excel

Как мы видели, вычисление среднего гармонического значения вручную может быть довольно утомительным, поскольку необходимо выполнить множество вычислений. И это становится еще сложнее, когда у вас есть большой объем данных. Поэтому для нахождения среднего гармонического значения мы рекомендуем использовать калькулятор или программу Excel.

Среднее гармоническое значение в Excel рассчитывается по формуле СРЕДНЕЕ.АРМО . То есть, чтобы вычислить среднее гармоническое набора данных, вам необходимо скопировать их в лист Excel и ввести все данные в функцию СРЕДНЕЕ.АРМО .

Например, чтобы получить среднее гармоническое значение упражнения, которое мы решили выше, вы должны написать в ячейке Excel =MEDIA.ARMO(7;10;15;6;11) .

Следует иметь в виду, что если какое-либо из значений равно нулю, функция вернет ошибку, поскольку среднее гармоническое набора статистических значений невозможно определить, если какое-либо из них равно нулю.