Гипергеометрическое распределение

К бенджамин андерсон 6 августа, 2023 Вероятность 0 комментариев

В этой статье мы объясняем, что такое гипергеометрическое распределение и как рассчитывается вероятность с помощью этого типа распределения. В сети вы найдете формулу гипергеометрического распределения, каковы ее характеристики, а также калькулятор для расчета вероятности гипергеометрического распределения.

Что такое гипергеометрическое распределение?

Гипергеометрическое распределение — это распределение вероятностей, которое описывает количество успешных случаев случайного извлечения без замены n элементов из популяции.

То есть гипергеометрическое распределение используется для расчета вероятности получения x успехов при извлечении n элементов из популяции без замены ни одного из них.

Гипергеометрическое распределение имеет три параметра:

N : количество элементов в популяции (N = 0, 1, 2,…).
K : максимальное количество случаев успеха (K = 0, 1, 2,…,N). Поскольку в гипергеометрическом распределении элемент можно считать только «успехом» или «неудачей», NK — это максимальное количество случаев отказа.
n : количество выполняемых выборок без замены.

$X \sim HG(N,K,n)$

Например, дискретная случайная величина X, имеющая гипергеометрическое распределение с параметрами N=8, K=5 и n=3, определяется следующим образом:

$X \sim HG(8,5,3)$

Формула гипергеометрического распределения

Формула гипергеометрического распределения представляет собой произведение комбинаторного числа K над x на комбинаторное число NK над nx , деленное на комбинаторное число N над n .

Где N — размер популяции, K — общее количество благоприятных случаев, n — количество экстракций без замены, а x — количество благоприятных случаев, для которых необходимо рассчитать вероятность возникновения.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать вероятность события переменной, которая следует гипергеометрическому распределению.

Пример гипергеометрического распределения

После того, как мы увидели определение и формулу гипергеометрического распределения, теперь мы шаг за шагом решим пример, чтобы вы знали, как рассчитать вероятность гипергеометрического распределения.

В мешочек кладем 20 синих шариков и 30 красных шариков, то есть всего внутри мешочка 50 шариков. Если вытащить 12 шаров, не заменив ни одного, найти вероятность вытащить 4 синих шара.

Первое, что нам нужно сделать для решения упражнения, это определить параметры гипергеометрического распределения. В этом случае общее количество элементов в популяции равно 50 ( N =50), максимальное количество благоприятных случаев — 20 ( K =20) и вытаскивается 12 шаров ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Мы хотим вычислить вероятность выпадения 4 синих шаров ( x =4), поэтому применяем формулу гипергеометрического распределения, подставляем переменные соответствующими значениями и выполняем расчет:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Калькулятор гипергеометрического распределения

Введите параметры гипергеометрического распределения в следующий онлайн-калькулятор, чтобы рассчитать вероятность наступления желаемого события.

Помните, что N — размер популяции, K — общее количество благоприятных случаев, n — размер выборки, а x — значение, для которого мы хотим найти вероятность того, что это произойдет.

Характеристики гипергеометрического распределения

Гипергеометрическое распределение обладает следующими свойствами:

Ожидаемое значение гипергеометрического распределения равно количеству элементов в выборке, умноженному на общее количество благоприятных случаев, деленное на количество элементов в популяции.

$E[X]=\cfrac{n\cdot K}{N}$

Мода гипергеометрического распределения — это значение, округленное в меньшую сторону от произведения n+1 , умноженного на K+1, на N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

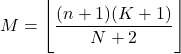
Дисперсию гипергеометрического распределения можно получить, используя следующее выражение:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Производящая функция момента гипергеометрического распределения выглядит следующим образом:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

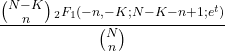
Характеристическая функция гипергеометрического распределения имеет следующий вид:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

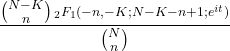
Вероятность появления заданного количества событий можно вычислить из вероятности предыдущего числа, используя рекурсию для гипергеометрического распределения:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Гипергеометрическое распределение и биномиальное распределение

Разница между гипергеометрическим распределением и биномиальным распределением заключается в замене. Гипергеометрическое распределение используется, когда выборки не заменяются, однако при биномиальном распределении заменяются выборки.

Например, если мы случайным образом вытягиваем пять карт в колоде и хотим вычислить вероятность получения определенной карты, и если мы не заменяем каждую взятую карту, мы должны использовать гипергеометрическое распределение для выполнения вычислений. Но если при удалении карты мы кладем ее обратно перед выполнением следующего извлечения, то для расчета вероятности необходимо использовать биномиальное распределение.

Когда число N велико, отношение n/N мало и число желаемых благоприятных случаев очень мало, мы можем использовать гипергеометрическое распределение как аппроксимацию биномиального распределения. Однако я не рекомендую этого делать, поскольку результат будет не таким надежным, и, кроме того, с помощью биномиального закона легче вычислять вероятности, чем с помощью гипергеометрического закона.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше