Как проверить предположения anova
Односторонний дисперсионный анализ — это статистический тест, используемый для определения того, существует ли значительная разница между средними значениями трех или более независимых групп.
Вот пример того, когда мы можем использовать однофакторный дисперсионный анализ:
Вы случайным образом делите класс из 90 учеников на три группы по 30 человек. Каждая группа в течение месяца использует разные методы обучения для подготовки к экзамену. В конце месяца все студенты сдают один и тот же экзамен.
Вы хотите знать, влияет ли техника обучения на результаты экзаменов. Итак, вы выполняете однофакторный дисперсионный анализ , чтобы определить, существует ли статистически значимая разница между средними баллами трех групп.
Прежде чем мы сможем выполнить однофакторный дисперсионный анализ, мы должны сначала убедиться, что выполняются три предположения.
1. Нормальность . Каждая выборка была взята из нормально распределенной популяции.
2. Равные дисперсии . Дисперсии совокупностей, из которых взяты выборки, равны.
3. Независимость . Наблюдения внутри каждой группы независимы друг от друга, а наблюдения внутри групп были получены методом случайной выборки.
Если эти предположения не выполняются, результаты нашего однофакторного дисперсионного анализа могут быть ненадежными.
В этой статье мы объясним, как проверить эти предположения и что делать, если какое-либо из них нарушено.
Предположение №1: нормальность
ANOVA предполагает, что каждая выборка была взята из нормально распределенной популяции.
Как проверить эту гипотезу в R:
Для проверки этой гипотезы мы можем использовать два подхода:
- Визуально проверьте гипотезу с помощью гистограмм или графиков QQ .
- Проверьте гипотезу, используя формальные статистические тесты, такие как Шапиро-Уилк, Колмогоров-Смиронов, Жарк-Барре или Д’Агостино-Пирсон.
Например, предположим, что мы набираем 90 человек для участия в эксперименте по снижению веса, в котором мы случайным образом назначаем 30 человек следовать программе А, программе Б или программе С в течение одного месяца. Чтобы увидеть, влияет ли программа на потерю веса, мы хотим выполнить однофакторный дисперсионный анализ. Следующий код демонстрирует, как проверить предположение о нормальности с помощью гистограмм, графиков QQ и теста Шапиро-Уилка.
1. Подберите модель ANOVA.
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. Создайте гистограмму значений ответа.
#create histogram
hist(data$weight_loss)
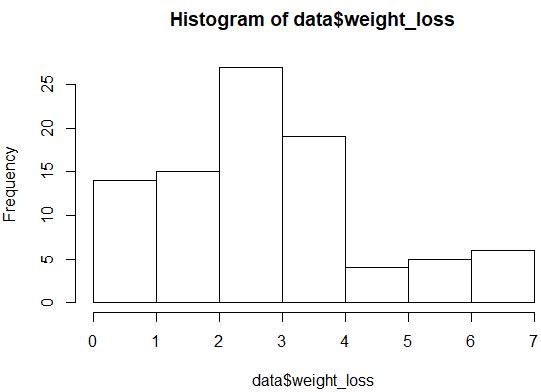
Распределение выглядит не совсем нормально (например, оно не имеет колоколообразной формы), но мы также можем создать график QQ, чтобы еще раз взглянуть на распределение.
3. Создайте график остатков QQ.
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

В общем, если точки данных лежат вдоль прямой диагональной линии на графике QQ, то набор данных, скорее всего, соответствует нормальному распределению. В этом случае мы видим заметное отклонение от линии по концам, что может указывать на неправильное распределение данных.
4. Выполните тест Шапиро-Уилка на нормальность.
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
Тест Шапиро-Уилка проверяет нулевую гипотезу о том, что выборки происходят из нормального распределения, против альтернативной гипотезы о том, что выборки не происходят из нормального распределения. В этом случае значение p теста составляет 0,005999 , что ниже уровня альфа 0,05. Это говорит о том, что выборки не подчиняются нормальному распределению.
Что делать, если это предположение не соблюдается:
В общем, однофакторный дисперсионный анализ считается достаточно устойчивым к нарушениям предположения о нормальности, если размеры выборки достаточно велики.
Кроме того, если у вас очень большие выборки, статистические тесты, такие как тест Шапиро-Уилка, почти всегда покажут вам, что ваши данные ненормальны. По этой причине зачастую лучше всего визуально проверять данные с помощью диаграмм, таких как гистограммы и графики QQ. Просто взглянув на графики, можно получить довольно хорошее представление о том, нормально ли распределяются данные или нет.
Если предположение о нормальности серьезно нарушено или вы просто хотите быть очень консервативным, у вас есть два варианта:
(1) Преобразуйте значения ответа ваших данных так, чтобы распределения распределялись более нормально.
(2) Выполните эквивалентный непараметрический тест, такой как тест Крускала-Уоллиса , который не требует предположения о нормальности.
Предположение № 2: равная дисперсия
ANOVA предполагает, что дисперсии совокупностей, из которых взяты выборки, равны.
Как проверить эту гипотезу в R:
Мы можем проверить эту гипотезу в R, используя два подхода:
- Визуально проверьте гипотезу, используя коробчатые диаграммы.
- Проверьте гипотезу, используя формальные статистические тесты, такие как тест Бартлетта.
Следующий код демонстрирует, как это сделать, используя тот же фальшивый набор данных о потере веса, который мы создали ранее.
1. Создайте коробчатые диаграммы.
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
Разницу в потере веса в каждой группе можно наблюдать по длине каждой коробчатой диаграммы. Чем длиннее поле, тем выше дисперсия. Например, мы видим, что дисперсия немного выше для участников программы C по сравнению с программой A и программой B.
2. Выполните тест Бартлетта.
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
Тест Бартлетта проверяет нулевую гипотезу о том, что выборки имеют равные дисперсии, против альтернативной гипотезы о том, что выборки не имеют равных дисперсий. В этом случае значение p теста составляет 0,01599 , что ниже уровня альфа 0,05. Это говорит о том, что не все выборки имеют одинаковую дисперсию.
Что делать, если это предположение не соблюдается:
В целом однофакторный дисперсионный анализ считается достаточно устойчивым к нарушениям предположения о равных дисперсиях, если каждая группа имеет одинаковый размер выборки.
Однако, если размеры выборки не одинаковы и это предположение серьезно нарушается, вместо этого вы можете запустить тест Крускала-Уоллиса , который представляет собой непараметрическую версию однофакторного дисперсионного анализа.
Предположение №3: Независимость
ANOVA предполагает:
- Наблюдения каждой группы независимы от наблюдений всех других групп.
- Наблюдения внутри каждой группы были получены методом случайной выборки.
Как проверить эту гипотезу:
Не существует формального теста, который можно использовать для проверки того, что наблюдения в каждой группе независимы и что они были получены путем случайной выборки. Единственный способ удовлетворить это предположение — использовать рандомизированный план.
Что делать, если это предположение не соблюдается:
К сожалению, вы мало что сможете сделать, если это предположение не выполняется. Проще говоря, если данные были собраны таким образом, что наблюдения в каждой группе не были независимыми от наблюдений в других группах, или если наблюдения внутри каждой группы не были получены с помощью рандомизированного процесса, результаты ANOVA не будут надежными. .
Если это предположение не выполняется, лучше всего воссоздать эксперимент, используя рандомизированный план.
Дальнейшее чтение:
Как выполнить односторонний дисперсионный анализ в R
Как выполнить однофакторный дисперсионный анализ в Excel
