Пять гипотез корреляции пирсона

Коэффициент корреляции Пирсона (также известный как «коэффициент корреляции момента продукта») измеряет линейную связь между двумя переменными.

Он всегда принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
• 0 указывает на отсутствие линейной корреляции между двумя переменными.
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Однако прежде чем рассчитывать коэффициент корреляции Пирсона между двумя переменными, мы должны убедиться, что выполняются пять допущений:

1. Уровень измерения: обе переменные следует измерять на уровне интервала или отношения .

2. Линейная связь: между двумя переменными должна существовать линейная связь.

3. Нормальность: обе переменные должны иметь примерно нормальное распределение.

4. Связанные пары. Каждое наблюдение в наборе данных должно иметь пару значений.

5. Никаких выбросов. В наборе данных не должно быть резких выбросов.

В этой статье мы даем объяснение каждому предположению, а также то, как определить, выполняется ли это предположение.

Гипотеза 1: Уровень измерения

Чтобы рассчитать коэффициент корреляции Пирсона между двумя переменными, обе переменные должны быть измерены на уровне интервала или отношения .

На следующем рисунке представлено краткое объяснение четырех уровней, на которых можно измерять переменные:

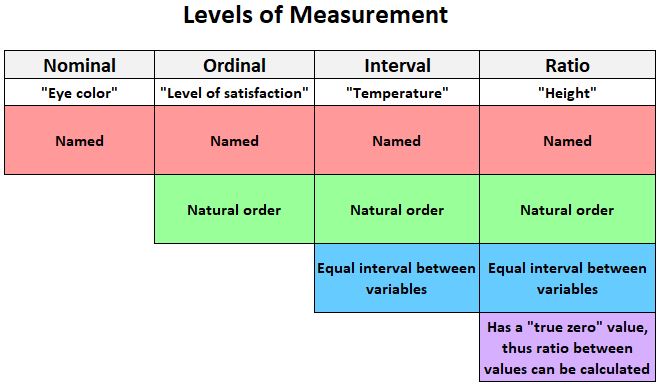
Вот несколько примеров переменных, которые можно измерить по интервальной шкале:

• Температура: Измеряется в градусах Фаренгейта или Цельсия.
• Кредитный рейтинг: измеряется от 300 до 850.
• Баллы SAT: измеряются от 400 до 1600.

Вот несколько примеров переменных, которые можно измерить по шкале отношений :

• Рост: Измеряется в сантиметрах, дюймах, футах и т. д.
• Вес: измеряется в килограммах, фунтах и т. д.
• Длина: Измеряется в сантиметрах, дюймах, футах и т. д.

Если переменные измеряются на порядковом уровне, то между ними необходимо рассчитать коэффициент корреляции Спирмена .

Связано: Уровни измерения: номинальный, порядковый, интервальный и коэффициент.

Гипотеза 2: Линейная зависимость

Чтобы рассчитать коэффициент корреляции Пирсона между двумя переменными, между двумя переменными должна существовать линейная связь.

Самый простой способ проверить эту гипотезу — просто создать диаграмму рассеяния двух переменных. Если точки на графике следуют примерно по прямой линии, то существует линейная зависимость:

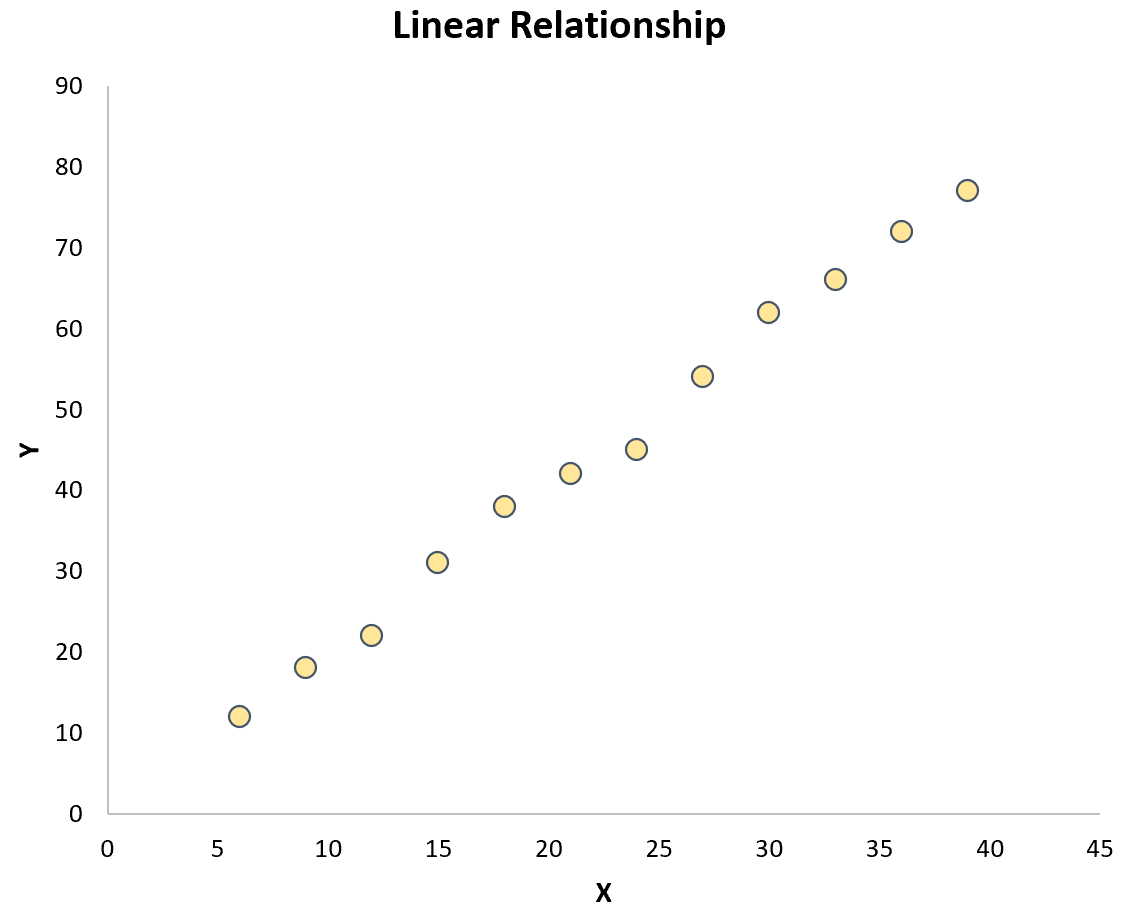
Однако если точки случайным образом разбросаны по графику или имеют какой-либо другой тип отношений (например, квадратичный), то между переменными не существует линейной зависимости:

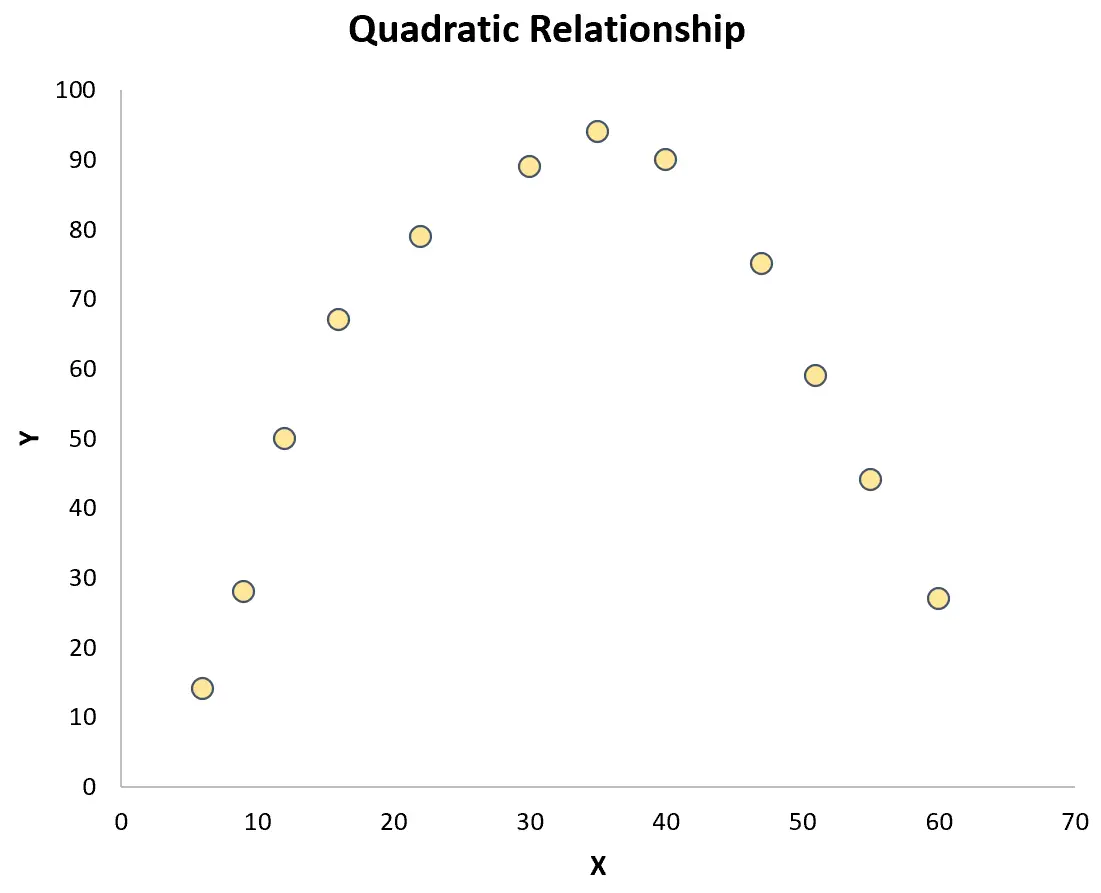
В этом случае коэффициент корреляции Пирсона не сможет адекватно отразить взаимосвязь между переменными.

Гипотеза 3: нормальность

Коэффициент корреляции Пирсона также предполагает, что две переменные примерно нормально распределены .

Вы можете проверить это предположение визуально, создав гистограмму или график QQ для каждой переменной.

1. Гистограмма

Если гистограмма набора данных имеет примерно колоколообразную форму, вполне вероятно, что данные распределены нормально.

2. QQLand

График QQ, сокращение от «квантиль-квантиль», представляет собой тип графика, который отображает теоретические квантили по оси X (т. е. где были бы ваши данные, если бы они следовали нормальному распределению) и квантили выборок по оси Y. (т.е. где на самом деле находятся ваши данные).

Если значения данных следуют примерно прямой линии, образующей угол 45 градусов, то предполагается, что данные распределены нормально.

Вы также можете выполнить формальный статистический тест, чтобы определить, является ли переменная нормально распределенной.

Если значение p теста ниже определенного уровня значимости (например, α = 0,05), то у вас есть достаточно доказательств, чтобы сказать, что данные не распределены нормально.

Для проверки нормальности обычно используются три статистических теста:

1. Тест Харке-Бера

• Как выполнить тест Жарка-Бера в Excel
• Как выполнить тест Жарка-Бера в R
• Как выполнить тест Жарка-Бера на Python

2. Тест Шапиро-Уилка

• Как выполнить тест Шапиро-Уилка в R
• Как выполнить тест Шапиро-Уилка на Python

3. Тест Колмогорова-Смирнова.

• Как выполнить тест Колмогорова-Смирнова в R
• Как выполнить тест Колмогорова-Смирнова в Python

Гипотеза 4: Родственные пары

Коэффициент корреляции Пирсона также предполагает, что каждое наблюдение в наборе данных должно иметь пару значений.

Эту гипотезу легко проверить. Например, если вы рассчитываете корреляцию между весом и ростом, просто убедитесь, что каждое наблюдение в наборе данных имеет меру веса и меру роста.

Гипотеза 5: Никаких выбросов

Коэффициент корреляции Пирсона также предполагает, что в наборе данных нет экстремальных выбросов, поскольку выбросы сильно влияют на расчет коэффициента корреляции.

Чтобы проиллюстрировать это, рассмотрим следующий набор данных:

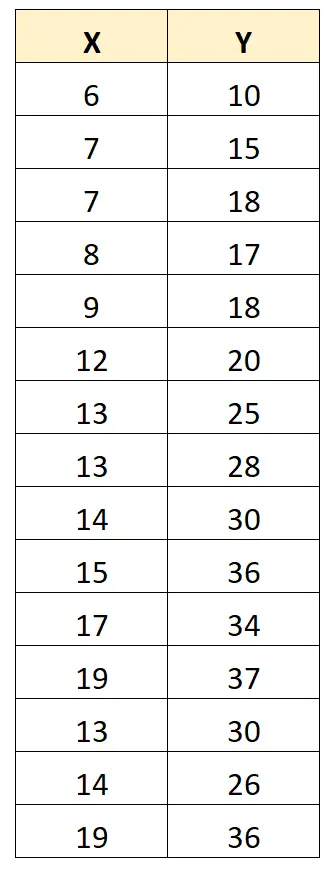
Коэффициент корреляции Пирсона между X и Y составляет 0,949 .

Однако предположим, что у нас есть выброс в наборе данных:

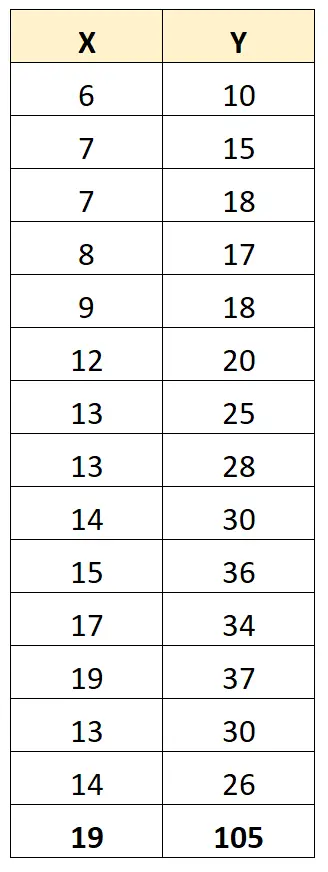
Коэффициент корреляции Пирсона между X и Y теперь составляет 0,711 .

Выброс значительно меняет коэффициент корреляции Пирсона между двумя переменными. В этом случае, возможно, имеет смысл удалить выброс из набора данных.

Связанный: Полное руководство: когда удалять выбросы в данных

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о корреляции Пирсона:

Введение в коэффициент корреляции Пирсона
Как сообщить о корреляции Пирсона в формате APA
Как вручную рассчитать коэффициент корреляции Пирсона