Как создать гистограмму остатков в r
Одним из основных предположений линейной регрессии является нормальное распределение остатков .
Один из способов визуально проверить это предположение — создать гистограмму остатков и наблюдать, соответствует ли распределение «колокольчатой форме», напоминающей нормальное распределение .
В этом руководстве представлен пошаговый пример создания гистограммы остатков для регрессионной модели в R.
Шаг 1. Создайте данные
Во-первых, давайте создадим несколько поддельных данных для работы:
#make this example reproducible set.seed(0) #createdata x1 <- rnorm(n=100, 2, 1) x2 <- rnorm(100, 4, 3) y <- rnorm(100, 2, 3) data <- data.frame(x1, x2, y) #view first six rows of data head(data) x1 x2 y 1 3.262954 6.3455776 -1.1371530 2 1.673767 1.6696701 -0.6886338 3 3.329799 2.1520303 5.8081615 4 3.272429 4.1397409 3.7815228 5 2.414641 0.6088427 4.3269030 6 0.460050 5.7301563 6.6721111
Шаг 2. Подберите регрессионную модель
Далее мы подгоним к данным модель множественной линейной регрессии :
#fit multiple linear regression model
model <- lm(y ~ x1 + x2, data=data)
Шаг 3. Создайте гистограмму остатков
Наконец, мы воспользуемся пакетом визуализации ggplot для создания гистограммы остатков модели:
#load ggplot2
library (ggplot2)
#create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
geom_histogram(fill = ' steelblue ', color = ' black ') +
labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ')
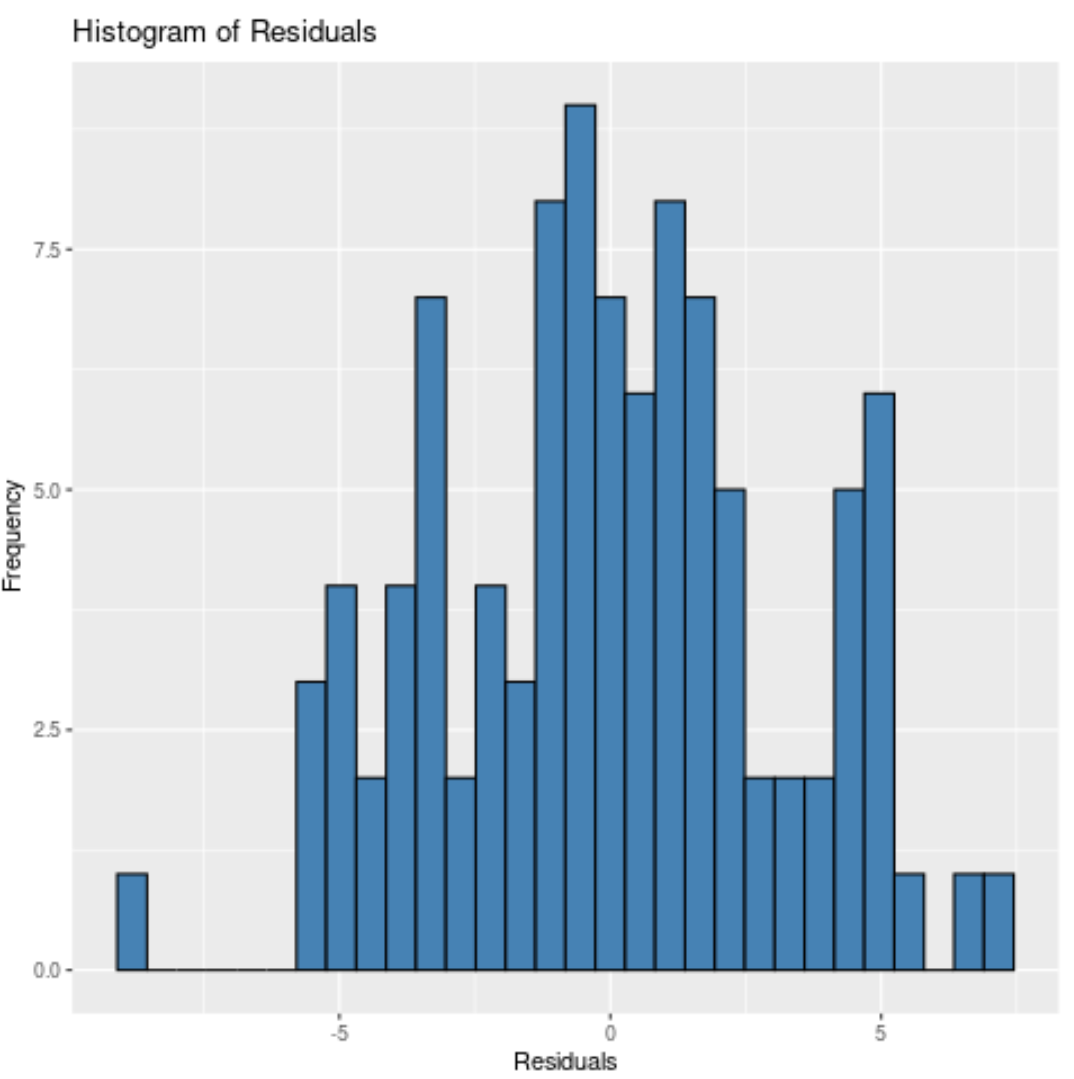
Обратите внимание, что мы также можем указать количество ячеек для размещения остатков, используя аргумент bin .
Чем меньше ячеек, тем шире будут столбцы на гистограмме. Например, мы могли бы указать 20 ячеек :
#create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
geom_histogram(bins = 20 , fill = ' steelblue ', color = ' black ') +
labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ')
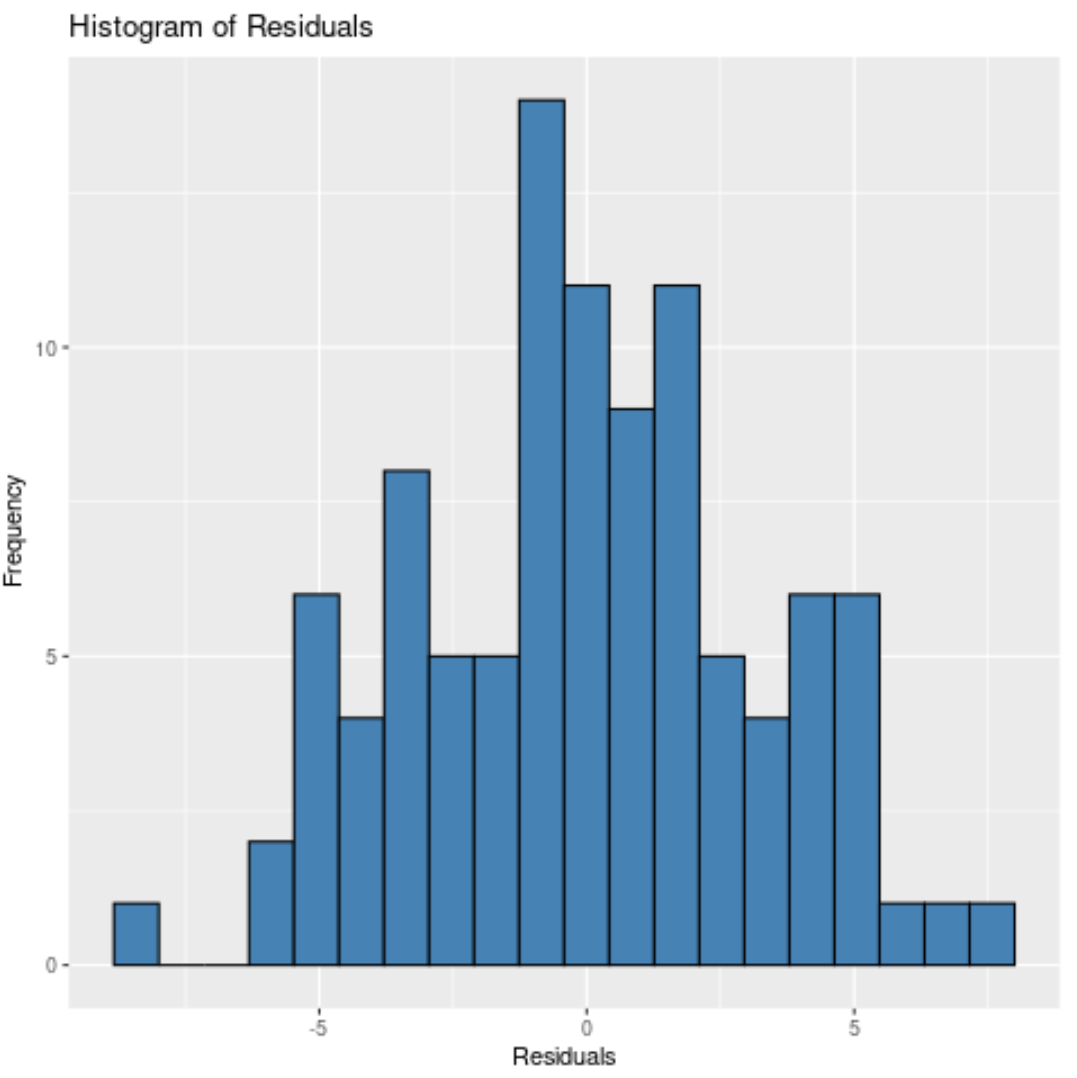
Или мы могли бы указать 10 ячеек :
#create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
geom_histogram(bins = 10 , fill = ' steelblue ', color = ' black ') +
labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ')
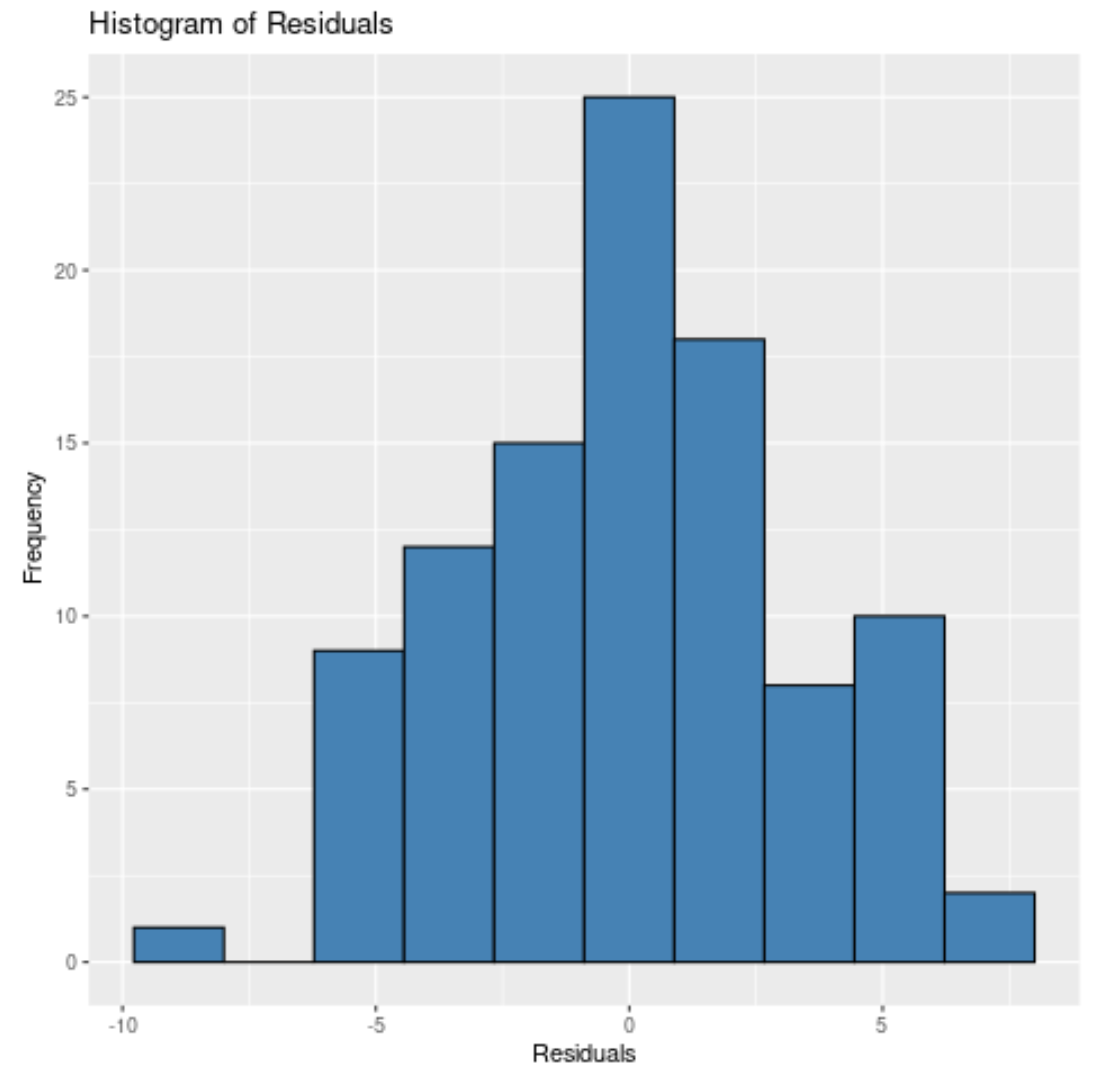
Независимо от того, сколько ящиков мы укажем, мы увидим, что остатки распределены примерно по нормальному закону.
Мы также могли бы провести формальный статистический тест, такой как Шапиро-Уилк, Колмогоров-Смирнов или Жарке-Бера, чтобы проверить нормальность.
Однако имейте в виду, что эти тесты чувствительны к большим размерам выборки – то есть они часто приходят к выводу, что остатки не являются нормальными, когда размер выборки велик.
По этой причине зачастую легче оценить нормальность, создав гистограмму остатков.