Как создать график qq в ggplot2 (с примером)

График QQ, сокращенно от «квантиль-квантиль», используется для оценки того, потенциально ли набор данных является результатом теоретического распределения.

В большинстве случаев этот тип графика используется для определения того, соответствует ли набор данных нормальному распределению.

Если данные распределены нормально, точки на графике QQ будут лежать на прямой диагональной линии.

И наоборот, если точки значительно отклоняются от прямой диагональной линии, то вероятность нормального распределения данных снижается.

Чтобы создать график QQ в ggplot2, вы можете использовать функции stat_qq() и stat_qq_line() следующим образом:

 library (ggplot2)

ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

В следующих примерах показано, как использовать этот синтаксис для создания графика QQ в двух разных сценариях.

Пример 1: График QQ для нормальных данных

Следующий код показывает, как сгенерировать нормально распределенный набор данных с 200 наблюдениями и создать график QQ для набора данных в R:

 library (ggplot2)

#make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
df <- data. frame (y=rnorm(200))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

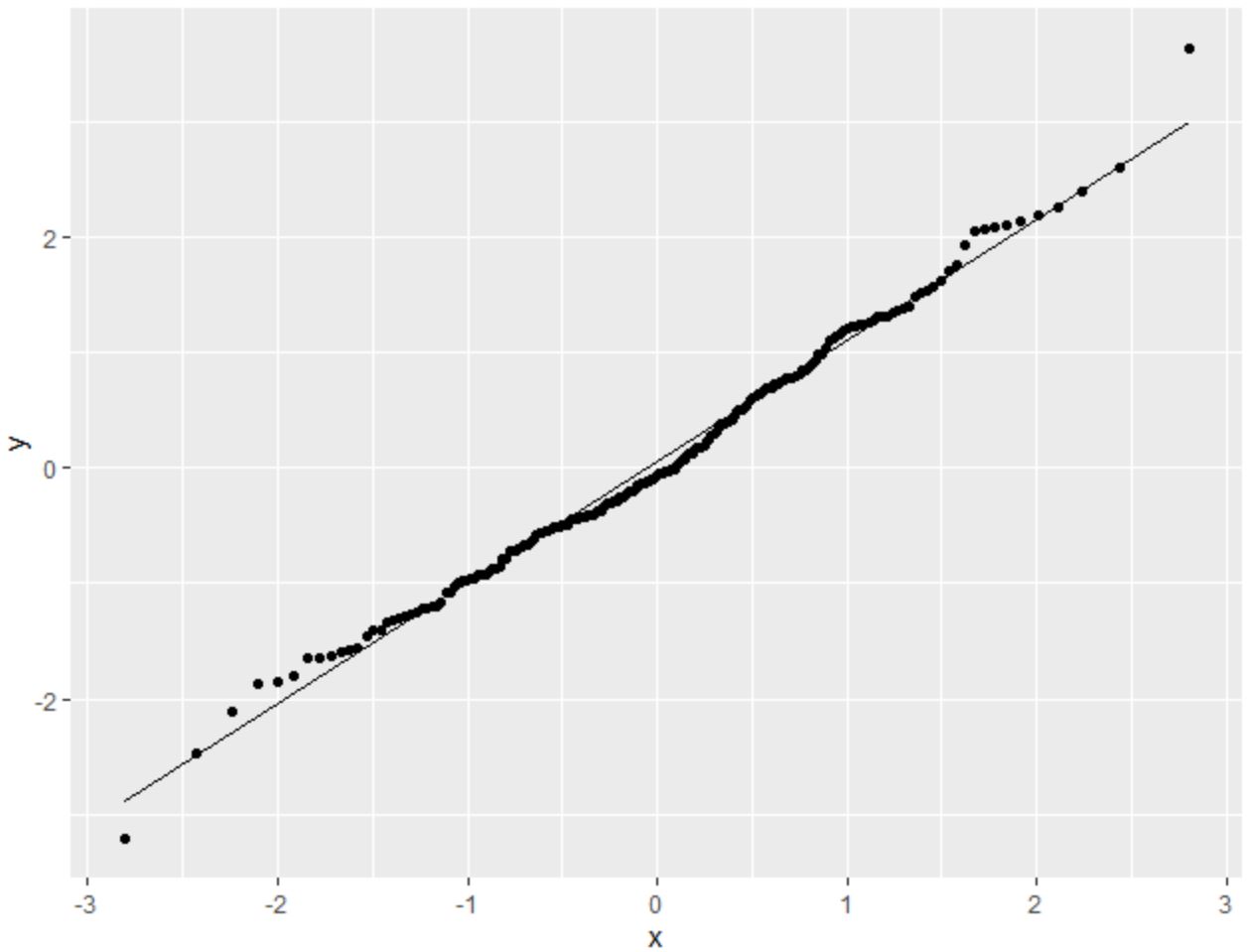
Мы видим, что точки лежат преимущественно вдоль прямой диагональной линии с небольшими отклонениями вдоль каждого из хвостов.

Основываясь на этом графике, мы можем предположить, что этот набор данных нормально распределен.

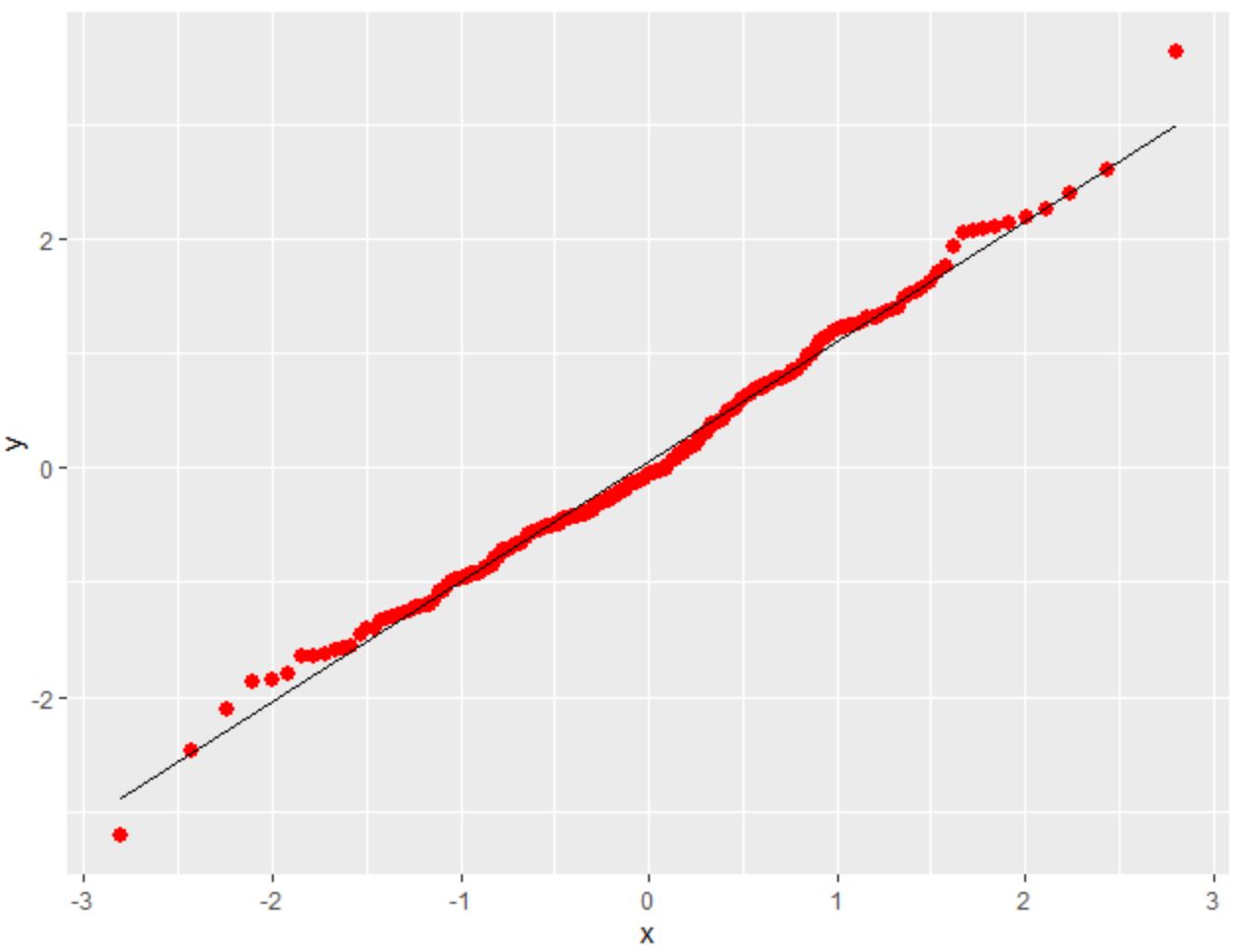
Обратите внимание, что мы также можем использовать аргументы цвета и размера, чтобы изменить цвет и размер точек на графике, если захотим:

 library (ggplot2)

#make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
df <- data. frame (y=rnorm(200))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq(size= 2.5 , color=' red ') + 
  stat_qq_line() 

Пример 2: График QQ для ненормальных данных

Следующий код показывает, как создать график QQ для набора данных, который соответствует экспоненциальному распределению с 200 наблюдениями:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
df <- data. frame (y=rexp( 200 , rate= 3 ))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

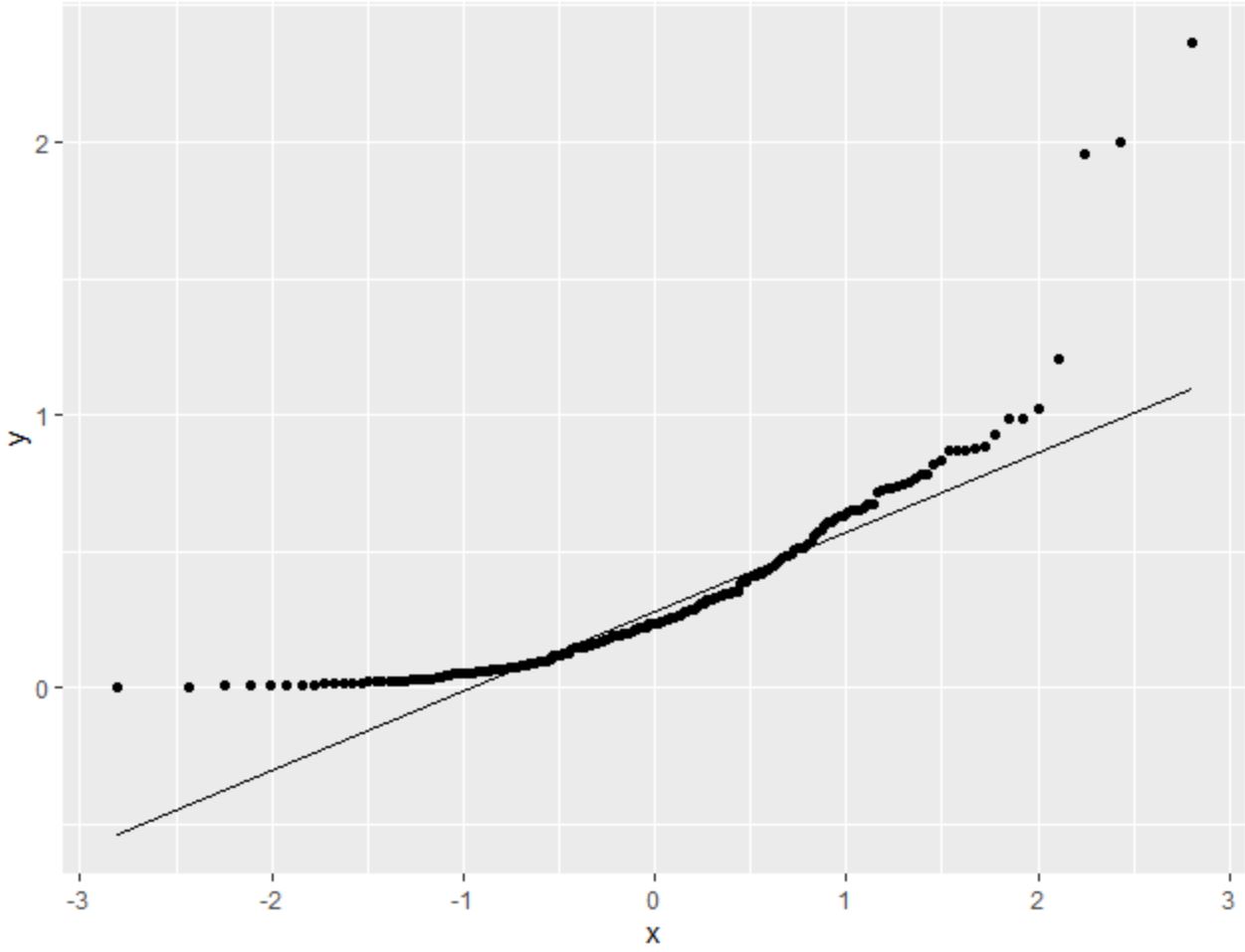
Мы видим, что точки значительно отклоняются от диагональной линии. Это ясно указывает на то, что набор данных обычно не распределяется.

Это должно иметь смысл, учитывая, что мы указали, что данные должны следовать экспоненциальному распределению.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в ggplot2:

Как построить несколько строк в ggplot2
Как построить среднее и стандартное отклонение в ggplot2
Как изменить цвет линий в ggplot2