Как выполнить t-тест для двух выборок в stata

Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей или нет.

В этом руководстве объясняется, как выполнить t-тест для двух выборок в Stata.

Пример: двухвыборочный t-критерий в Stata

Исследователи хотят знать, вызывает ли новая обработка топлива изменение среднего расхода топлива на галлон определенного автомобиля. Чтобы проверить это, они проводят эксперимент, в ходе которого 12 автомобилей получают новое топливо, а 12 — нет.

Выполните следующие шаги, чтобы выполнить t-критерий с двумя выборками, чтобы определить, существует ли разница в среднем расходе миль на галлон между этими двумя группами.

Шаг 1: Загрузите данные.

Сначала загрузите данные, набрав use https://www.stata-press.com/data/r13/fuel3 в командном поле и нажав Enter.

Шаг 2: Просмотрите необработанные данные.

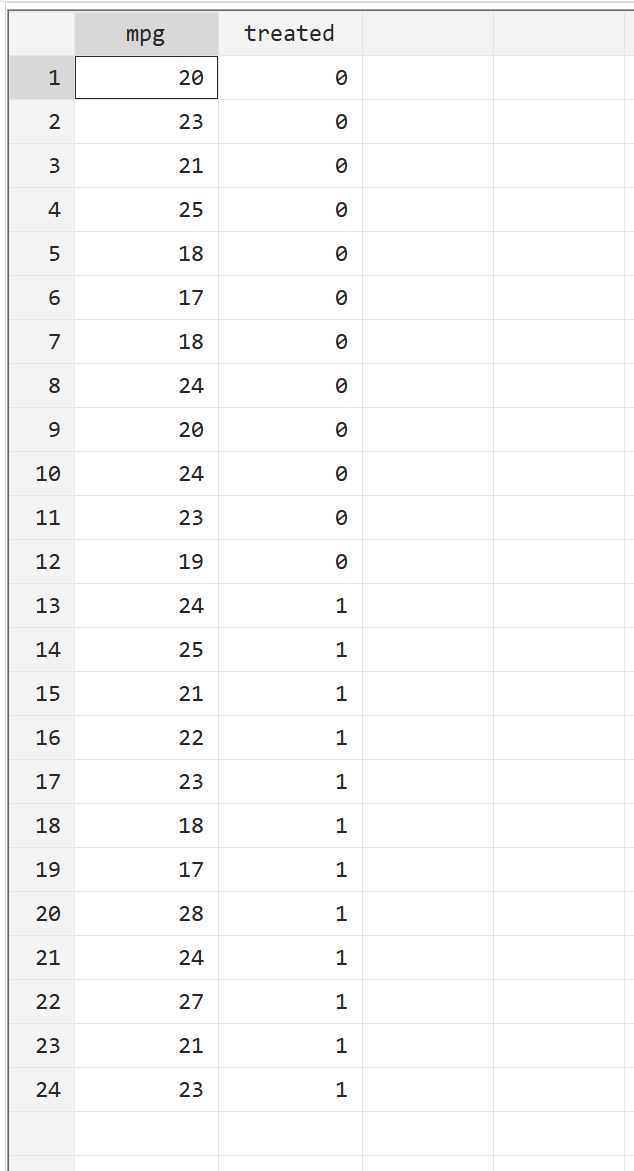
Прежде чем проводить t-критерий с двумя выборками, давайте сначала посмотрим на необработанные данные. В верхней строке меню выберите «Данные» > «Редактор данных» > «Редактор данных (Обзор)» . В первом столбце, mpg , отображается расход топлива для данного автомобиля. Второй столбец, обработанный , указывает, прошел ли автомобиль обработку топливом (0 = нет, 1 = да).

Шаг 3: Визуализируйте данные.

Далее давайте визуализируем данные. Мы создадим коробчатые диаграммы для отображения распределения значений миль на галлон для каждой группы.

В верхней строке меню выберите «Диаграммы» > «Ящики» . В разделе переменных выберите mpg :

Затем в подзаголовке «Категории» в разделе «Переменная группировки» выберите «Обработано» :

Нажмите ОК . Автоматически отобразится диаграмма с двумя коробчатыми диаграммами:

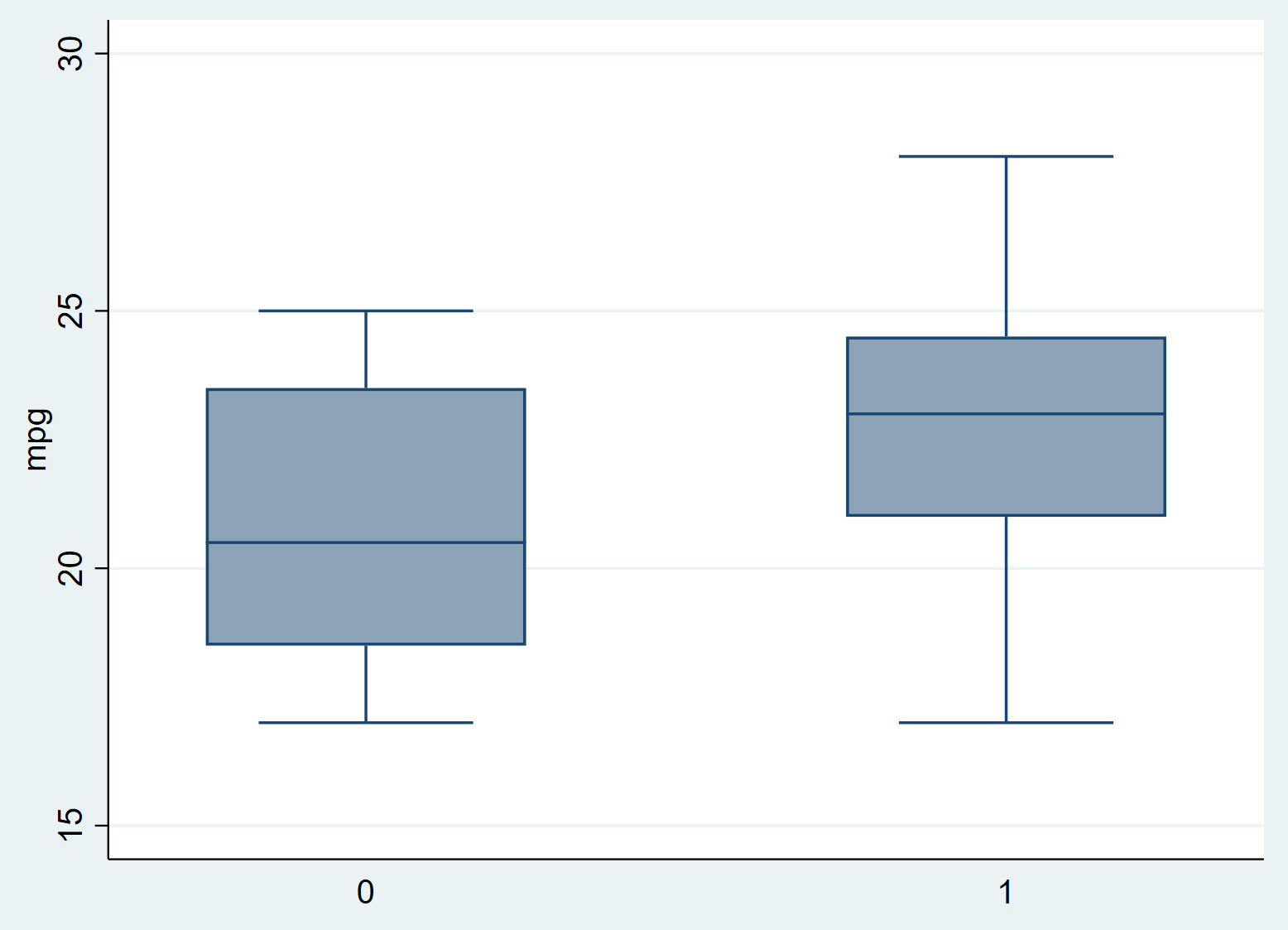
Мы сразу видим, что расход миль на галлон выше в группе, получавшей лечение (1), по сравнению с группой, не получавшей лечения (0), но нам необходимо провести t-тест для двух выборок, чтобы увидеть, являются ли эти различия статистически значимыми. .

Шаг 4. Выполните t-тест для двух выборок.

В верхней строке меню выберите «Статистика» > «Сводки, таблицы и тесты» > «Классические проверки гипотез» > «t-тест» (проверка сравнения средних) .

Выберите «Два образца с использованием групп» . В качестве имени переменной выберите mpg . В поле «Имя групповой переменной» выберите «Обработано» . В разделе «Уровень уверенности» выберите нужный уровень. Значение 95 соответствует уровню значимости 0,05. Мы оставим значение 95. Наконец, нажмите «ОК» .

Будут отображены результаты двух выборочных t-тестов:

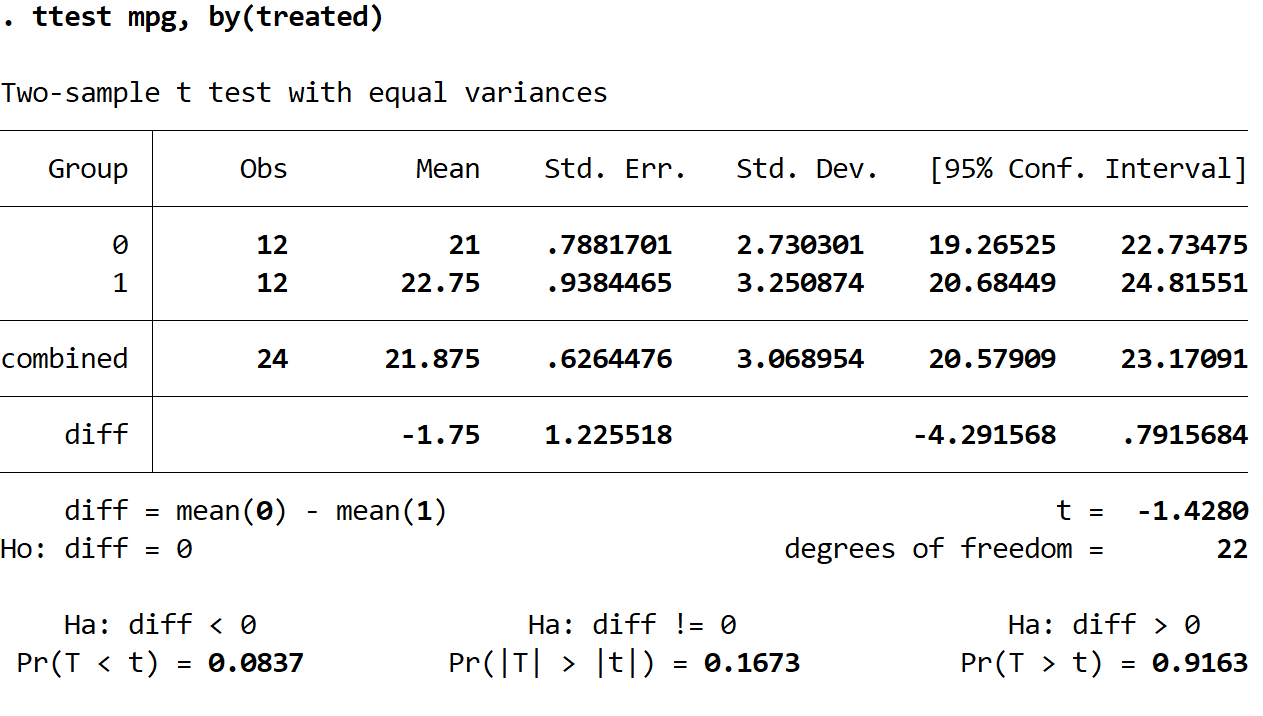
По каждой группе мы получаем следующую информацию:

Obs: Количество наблюдений. В каждой группе по 12 наблюдений.

Среднее: Среднее количество миль на галлон. В группе 0 средний показатель равен 21. В группе 1 средний показатель составляет 22,75.

Стандарт. Err: стандартная ошибка, рассчитываемая как σ / √ n

Стандарт. Dev: стандартное отклонение миль на галлон.

95% Конф. Диапазон: 95% доверительный интервал для истинного среднего показателя по популяции в милях на галлон.

t: тестовая статистика двухвыборочного t-критерия.

степени свободы: степени свободы, используемые для теста, рассчитываются как n-2 = 24-2 = 22.

Значения p для трех разных двухвыборочных t-тестов показаны внизу результатов. Поскольку мы хотим понять, отличается ли средний расход миль на галлон между двумя группами, мы посмотрим на результаты промежуточного теста (в котором альтернативной гипотезой является Ha:diff !=0), значение p которого равно 0,1673. .

Поскольку это значение не ниже нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу. У нас недостаточно доказательств, чтобы сказать, что истинное среднее количество миль на галлон в этих двух группах различается.

Шаг 5: Сообщите о результатах.

Наконец, мы сообщим о результатах наших двух выборочных t-тестов. Вот пример того, как это сделать:

На 24 автомобилях был проведен Т-тест с двумя выборками, чтобы определить, вызвала ли новая обработка топлива разницу в среднем пробеге на галлон. В каждой группе было по 12 машин.

Результаты показали, что средний расход миль на галлон не различался между двумя группами (t = -1,428 с df = 22, p = 0,1673) при уровне значимости 0,05.

95% доверительный интервал для истинной разницы в средних значениях популяции дал интервал (-4,29, 0,79).