Как выполнить t-тест для двух выборок в excel
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей или нет.
В этом руководстве объясняется, как выполнить t-тест для двух выборок в Excel.
Как выполнить t-тест для двух выборок в Excel
Предположим, исследователи хотят знать, имеют ли два разных вида растений в данной стране одинаковую среднюю высоту. Поскольку обход и измерение каждого растения занял бы слишком много времени, они решили взять по 20 образцов каждого вида.
На следующем изображении показана высота (в дюймах) каждого растения в каждом образце:
Мы можем выполнить t-критерий с двумя выборками, чтобы определить, имеют ли два вида одинаковый средний рост, выполнив следующие шаги:
Шаг 1: Определите, равны ли дисперсии генеральной совокупности .
Когда мы выполняем t-тест для двух выборок, мы должны сначала решить, будем ли мы предполагать, что две совокупности имеют равные или неравные дисперсии. Как правило, мы можем предположить, что популяции имеют равные дисперсии, если отношение наибольшей выборочной дисперсии к наименьшей выборочной дисперсии меньше 4:1.
Мы можем найти дисперсию для каждого образца, используя функцию Excel =VAR.S(Диапазон ячеек) , как показано на следующем изображении:
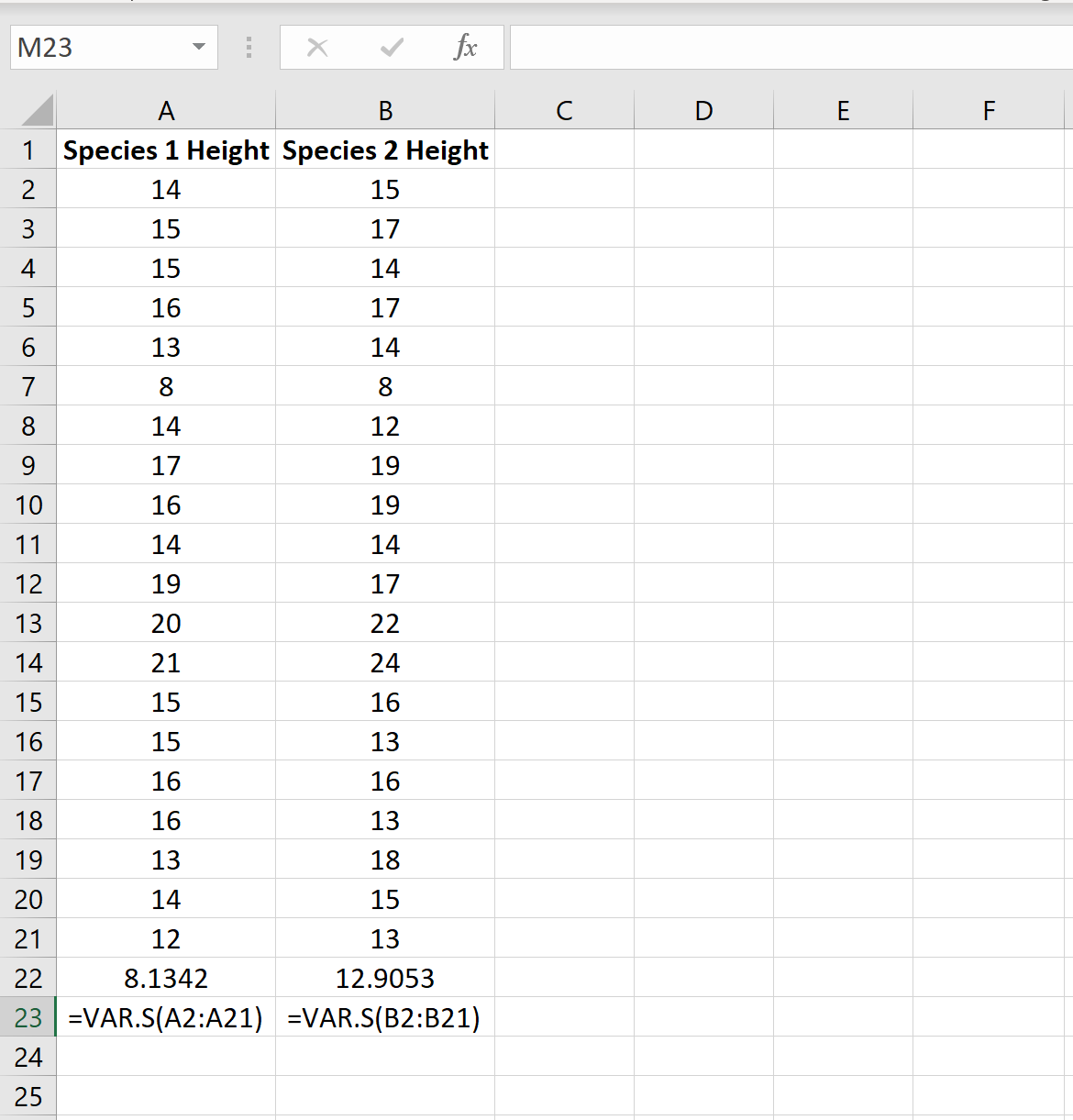
Отношение наибольшей выборочной дисперсии к наименьшей выборочной дисперсии составляет 12,9053/8,1342 = 1,586 , что меньше 4. Это означает, что мы можем предположить, что генеральные дисперсии равны.
Шаг 2. Откройте пакет инструментов анализа .
На вкладке «Данные» верхней ленты нажмите «Анализ данных».
Если вы не видите эту опцию, вам сначала необходимо загрузить Analysis ToolPak , который совершенно бесплатен.
Шаг 3: Выберите подходящий тест для использования.
Выберите вариант с надписью t-test: две выборки с одинаковыми дисперсиями , а затем нажмите «ОК».
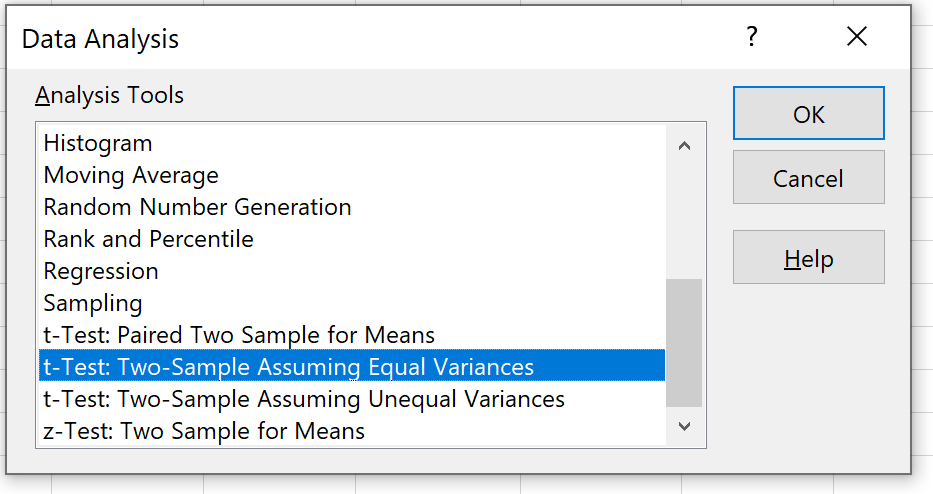
Шаг 4: Введите необходимую информацию .
Введите диапазон значений для переменной 1 (наша первая выборка), переменной 2 (наша вторая выборка), гипотетической средней разницы (в данном случае мы ставим «0», потому что хотим знать, равна ли истинная средняя разница в популяции 0) и выходной диапазон, в котором мы хотели бы видеть результаты t-теста. Затем нажмите ОК.
Шаг 5: Интерпретируйте результаты .
После того, как вы нажмете «ОК» на предыдущем шаге, отобразятся результаты t-теста.
Вот как интерпретировать результаты:
Среднее: это среднее значение каждого образца. Образец 1 имеет среднюю высоту 15,15 , а образец 2 — среднюю высоту 15,8 .
Дисперсия: это дисперсия для каждого образца. Выборка 1 имеет дисперсию 8,13 , а выборка 2 — 12,90 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки содержат по 20 наблюдений (например, по 20 отдельных растений в каждой выборке).
Объединенная дисперсия: число, рассчитанное путем «объединения» дисперсий каждой выборки по формуле s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 — 2), что оказывается 10,51974 . Это число затем используется при расчете статистики t -теста.
Гипотетическая средняя разница: число, о котором мы «выдвигаем гипотезу», представляет собой разницу между средними значениями двух совокупностей. В данном случае мы выбрали 0, потому что хотим проверить, равна ли разница между средними значениями двух совокупностей 0, например, нет ли разницы.
df: Степени свободы для t-критерия, рассчитанные как n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: статистика теста t , рассчитываемая как t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
В этом случае t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
Двусторонний P(T<=t): значение p для двустороннего t-критерия. В этом случае р = 0,530047 . Это намного больше, чем альфа = 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что средства двух популяций различны.
t Двусторонний критический критерий: это критическое значение теста, определяемое путем определения значения в таблице t-распределения, которое соответствует двустороннему критерию с альфа = 0,05 и df = 38. Оно оказывается равным 2, 024394 . Поскольку наша статистика t- теста меньше этого значения, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что средства двух популяций различны.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие типы t-тестов в Excel:
Как выполнить t-критерий для одной выборки в Excel
Как выполнить t-критерий для парных выборок в Excel
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше