Как выполнить t-тест для двух выборок в spss

Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей или нет.

В этом руководстве объясняется, как выполнить t-тест для двух выборок в SPSS.

Пример: двухвыборочный t-критерий в SPSS

Исследователи хотят знать, вызывает ли новая обработка топлива изменение среднего пробега на галлон данного автомобиля. Чтобы проверить это, они проводят эксперимент, в ходе которого 12 автомобилей получают новое топливо, а 12 — нет.

На следующем снимке экрана показано количество миль на галлон каждого автомобиля вместе с группой, к которой он принадлежит (0 = без обработки топлива, 1 = обработка топлива):

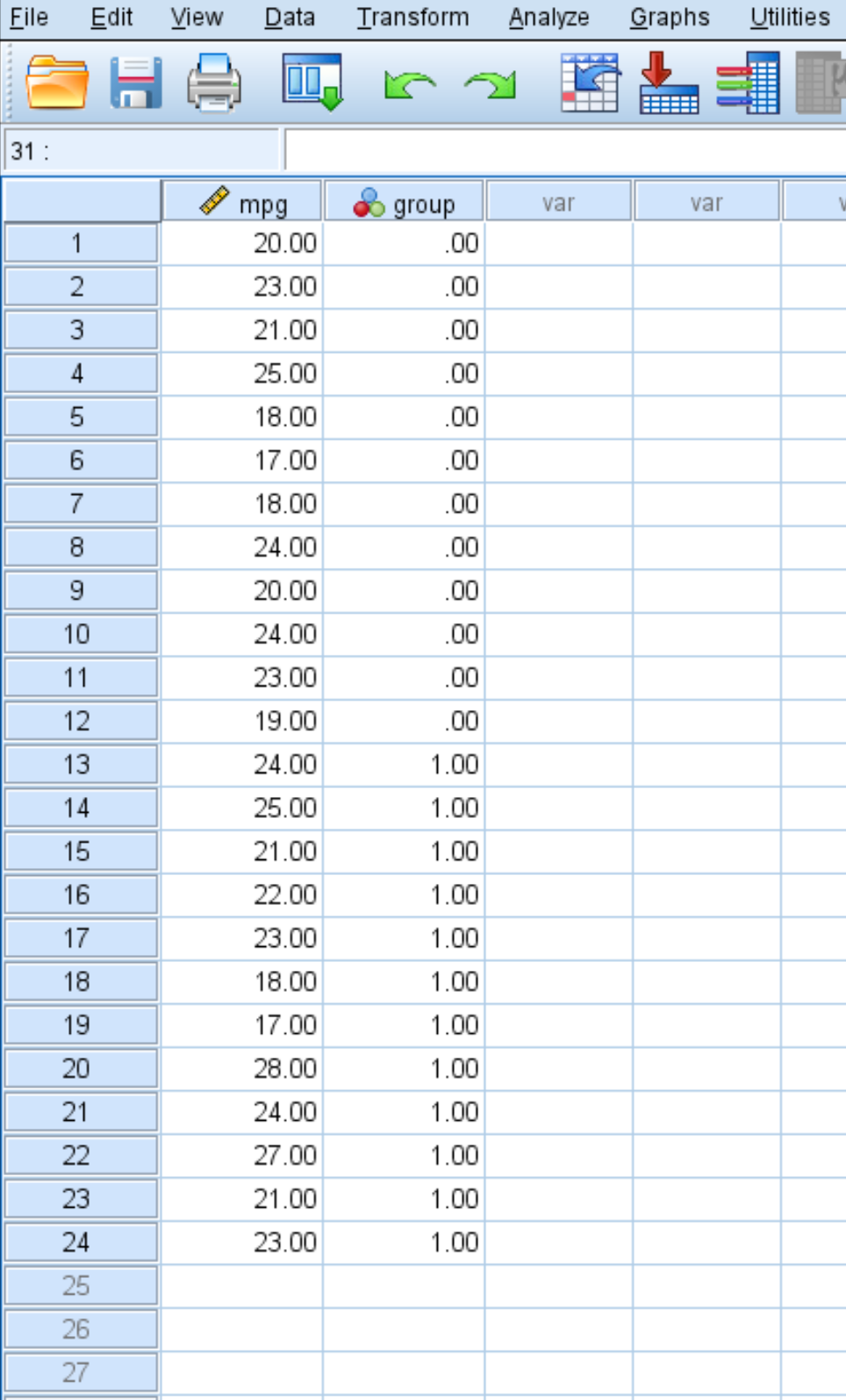
Используйте следующие шаги, чтобы выполнить двухвыборочный t-критерий, чтобы определить, существует ли разница в среднем расходе миль на галлон между этими двумя группами, на основе следующих нулевых и альтернативных гипотез:

• H ₀ : μ ₁ = μ ₂ (среднее количество миль на галлон между двумя популяциями одинаково)
• H ₁ : μ ₁ ≠ μ ₂ (средний расход миль на галлон между двумя популяциями не равен)

Используйте уровень значимости α = 0,05.

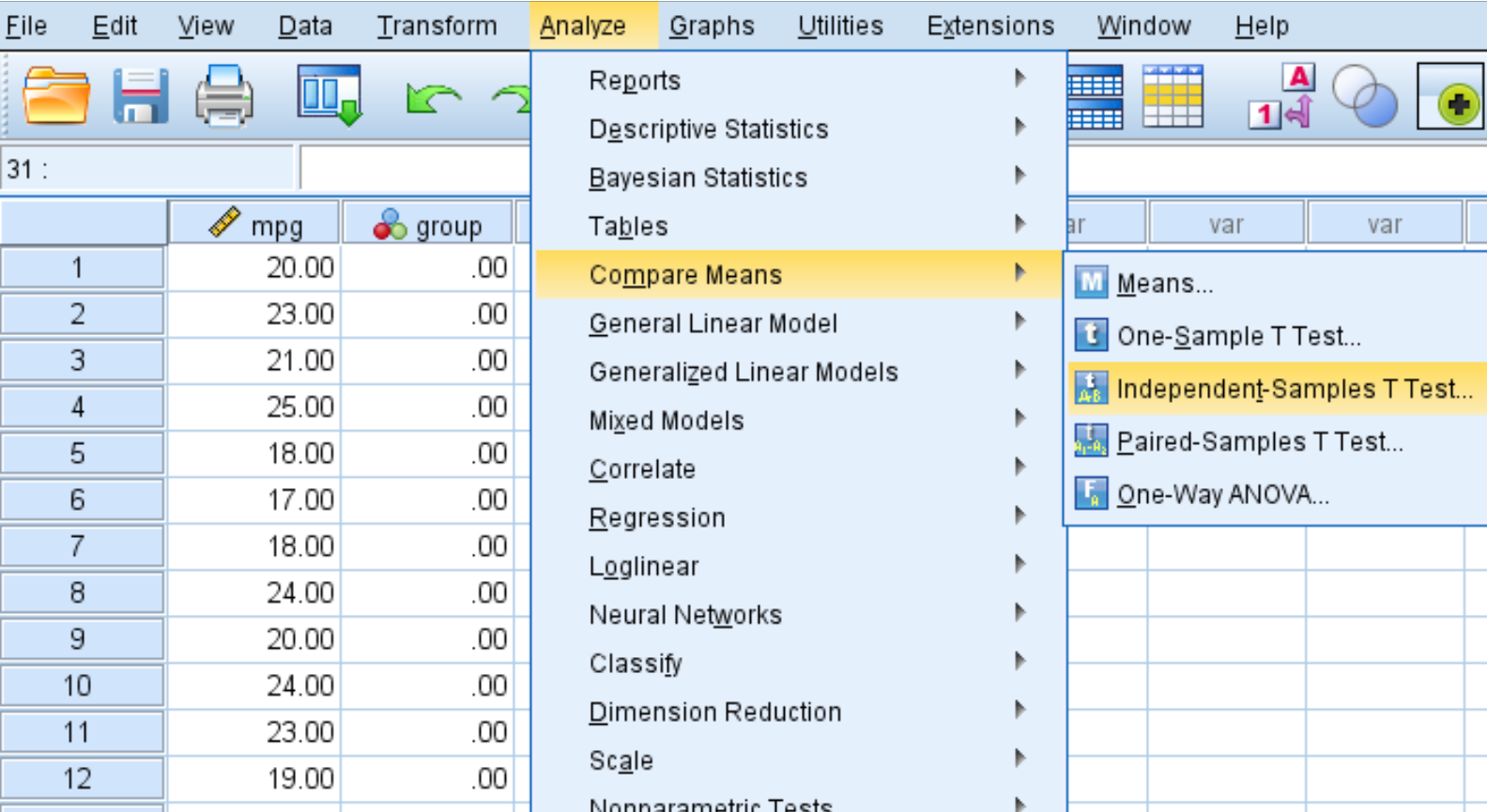
Шаг 1. Выберите опцию T-тест для независимых образцов.

Перейдите на вкладку «Анализ» , затем «Сравнить средние» , затем «Т-критерий независимых выборок »:

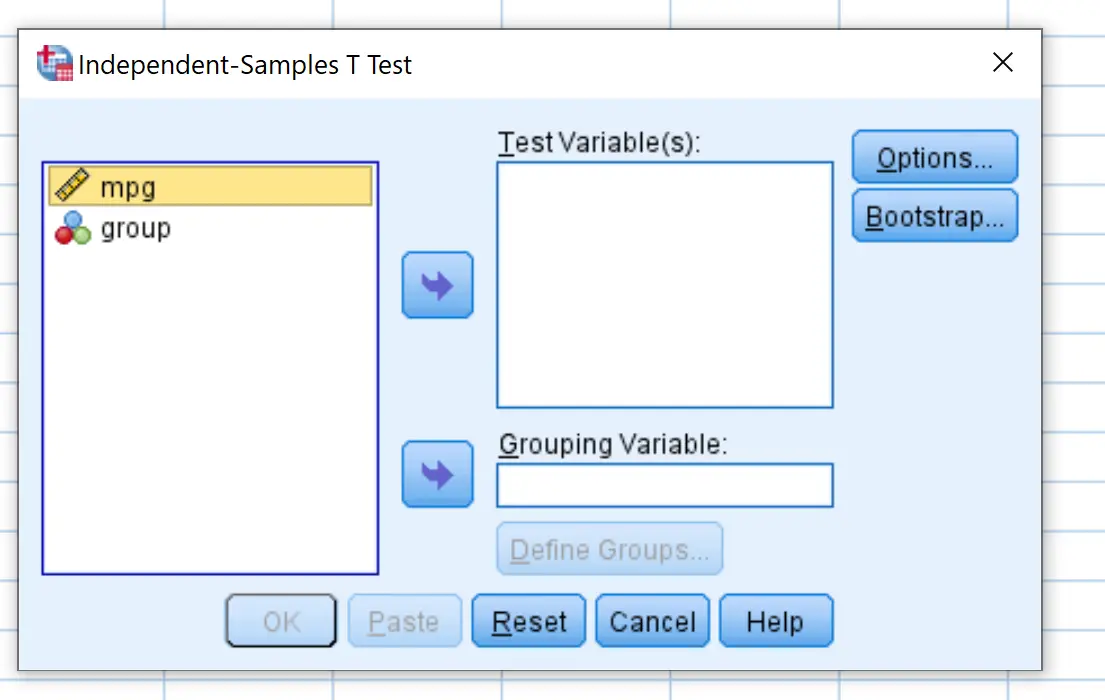
Шаг 2. Введите значения, необходимые для выполнения двухвыборочного t-теста.

После того, как вы нажмете T-тест для независимых выборок , появится следующее окно:

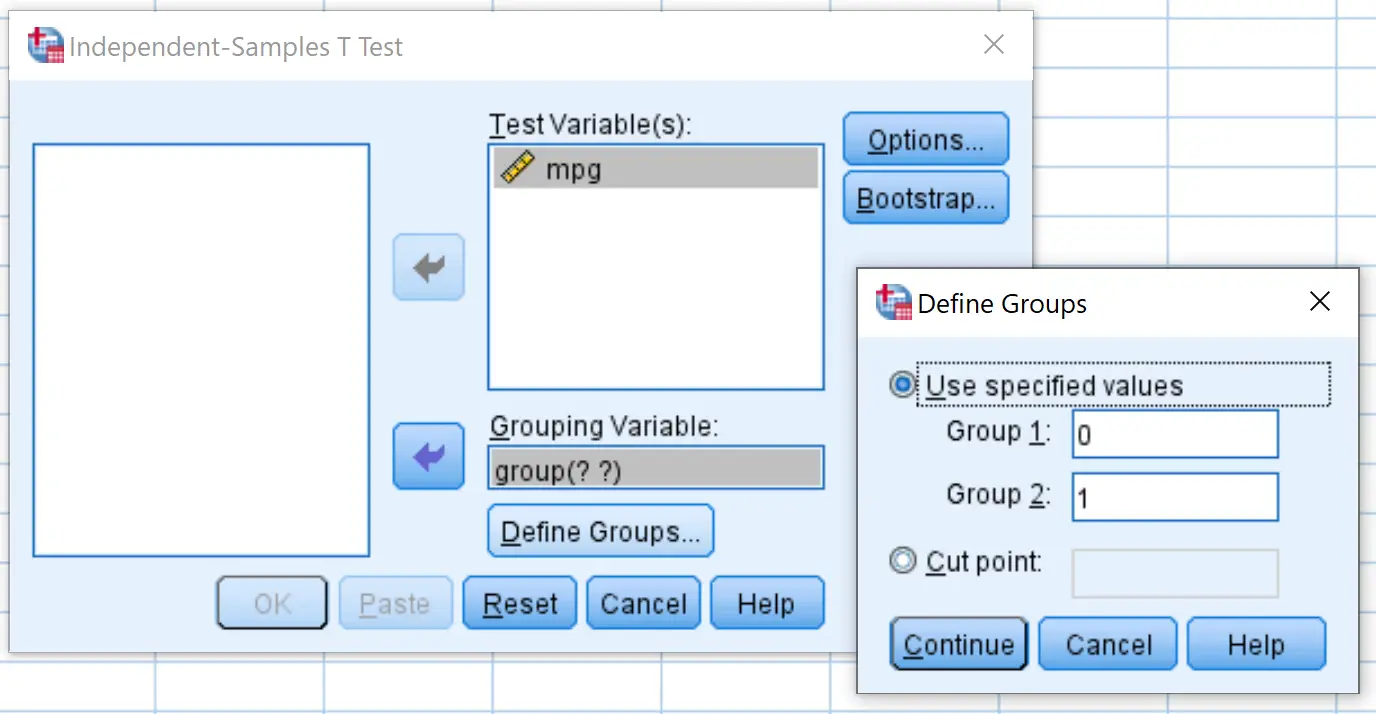
Перетащите расход топлива на галлон в поле « Тестовые переменные» и сгруппируйте его в поле « Переменная группировки» . Затем нажмите «Определить группы» и определите группу 1 как строки со значением 0, а группу 2 — как строки со значением 1. Затем нажмите «ОК» .

Шаг 3: Интерпретируйте результаты.

Как только вы нажмете «ОК» , отобразятся результаты двух выборочных t-тестов:

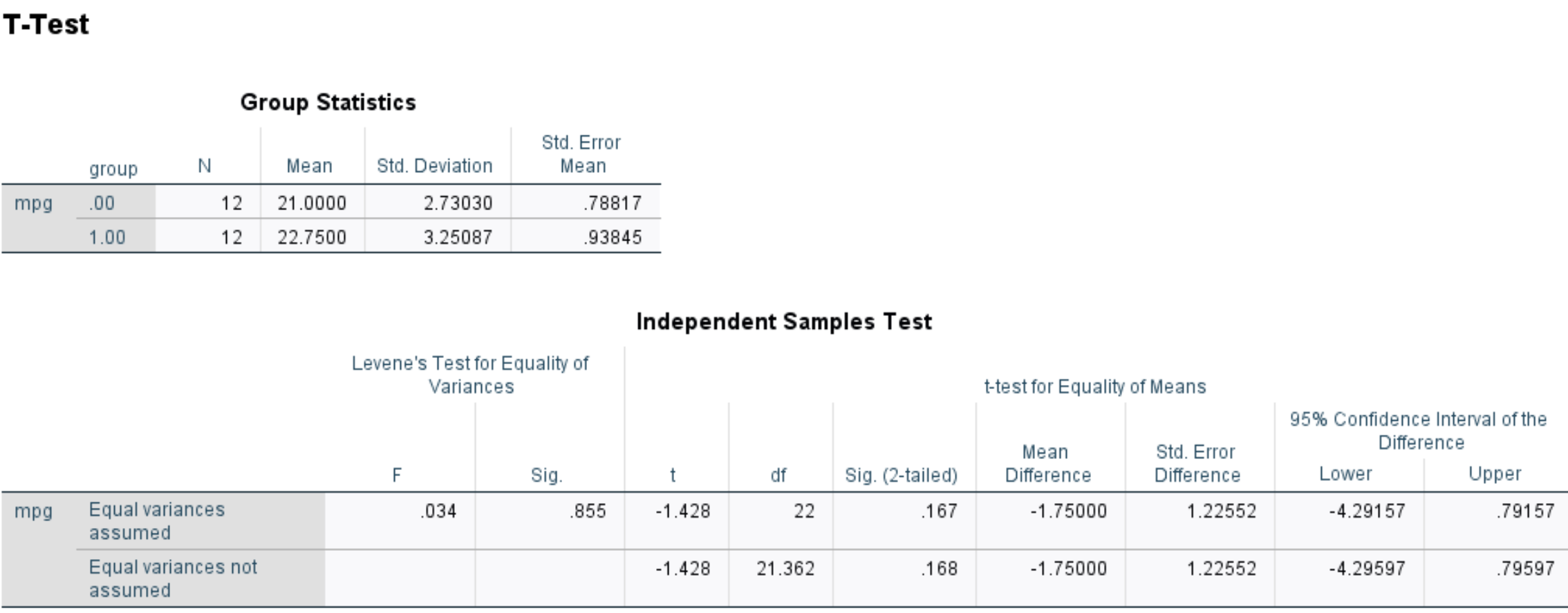
В первой таблице отображена следующая сводная статистика для двух групп:

• N: Размер выборки
• Среднее: средний расход автомобилей в каждой группе.
• Стандарт. Отклонение: стандартное отклонение расхода миль на галлон автомобилей в каждой группе.
• Стандарт. Средняя ошибка: стандартная ошибка среднего значения миль на галлон, рассчитанная в с/√n.

Во второй таблице показаны результаты двухвыборочного t-критерия. В первой строке показаны результаты теста, если предположить, что дисперсия между двумя группами одинакова. Вторая строка показывает результаты теста, если вы не делаете этого предположения.

При этом обе версии теста дают практически одинаковые результаты. Итак, мы просто будем ссылаться на результаты первой строки:

• t: Статистика теста равна -1,428.
• df: Степени свободы, рассчитанные как n ₁ + n ₂ -2 = 12+12-2 = 22.
• Сиг. (двусторонний): двустороннее значение p, которое соответствует значению -1,428 с df=22.
• Средняя разница: разница между двумя выборками означает
• Стандарт. Ошибка разности: стандартная ошибка средней разницы.
• 95% ДИ разницы: 95% доверительный интервал для истинной разницы между средними значениями двух популяций.

Поскольку значение p теста (0,167) не менее 0,05, мы не можем отвергнуть нулевую гипотезу. У нас недостаточно доказательств, чтобы сказать, что истинный средний расход миль на галлон различается между автомобилями, прошедшими лечение, и автомобилями, которые этого не делают.