Как выполнить двумерный анализ в python: с примерами

Термин двумерный анализ относится к анализу двух переменных. Вы можете это запомнить, потому что приставка «би» означает «два».

Цель двумерного анализа — понять взаимосвязь между двумя переменными.

Существует три распространенных способа выполнения двумерного анализа:

1. Облака точек

2. Коэффициенты корреляции

3. Простая линейная регрессия

В следующем примере показано, как выполнить каждый из этих типов двумерного анализа в Python, используя следующий DataFrame pandas, который содержит информацию о двух переменных: (1) часах, потраченных на обучение, и (2) баллах на экзамене, полученных 20 разными студентами:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Облака точек

Мы можем использовать следующий синтаксис, чтобы создать диаграмму рассеяния учебных часов и результатов экзамена:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

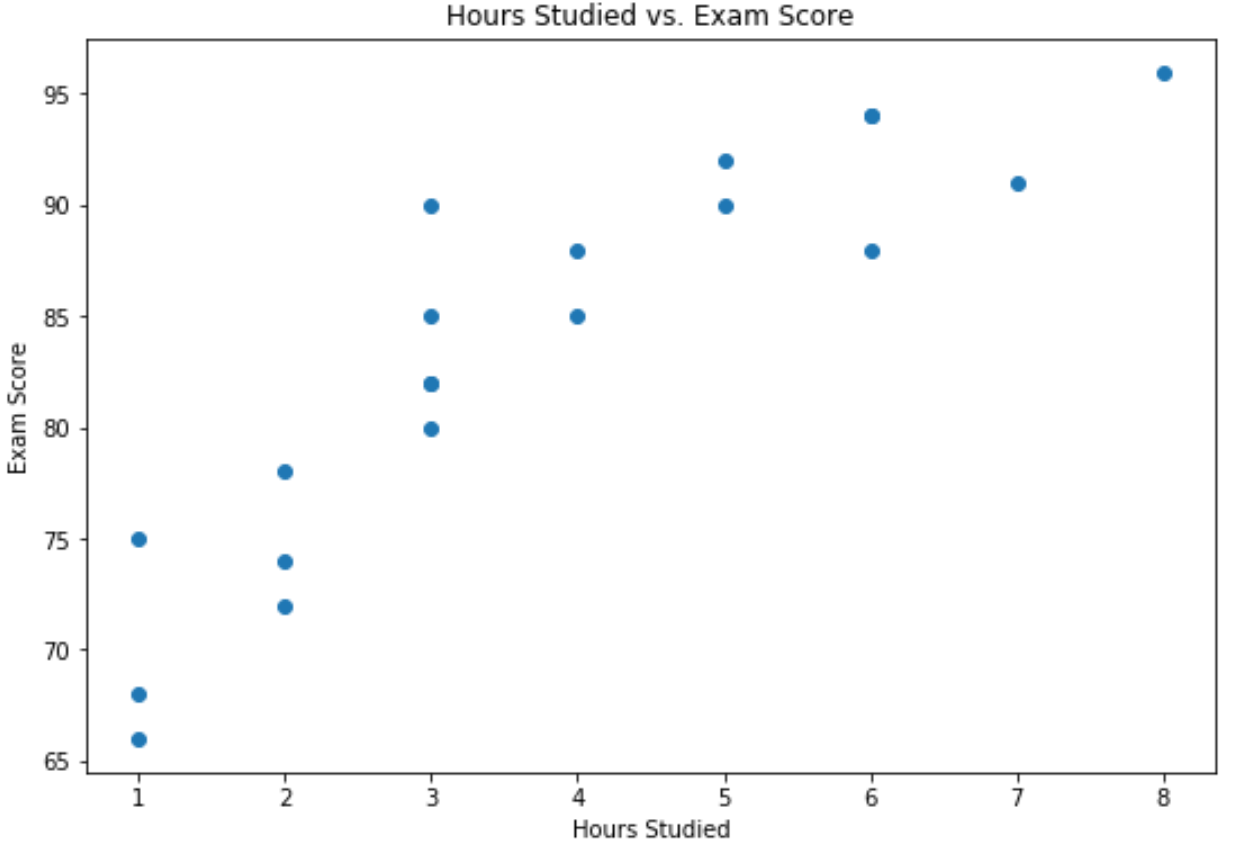
По оси X показано количество учебных часов, а по оси Y — оценка, полученная на экзамене.

График показывает, что между двумя переменными существует положительная связь: по мере увеличения количества учебных часов результаты экзаменов также имеют тенденцию к увеличению.

2. Коэффициенты корреляции

Коэффициент корреляции Пирсона — это способ количественной оценки линейной зависимости между двумя переменными.

Мы можем использовать функцию corr() в pandas для создания корреляционной матрицы:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

Коэффициент корреляции оказывается равным 0,891 . Это указывает на сильную положительную корреляцию между количеством учебных часов и оценкой на экзамене.

3. Простая линейная регрессия

Простая линейная регрессия — это статистический метод, который мы можем использовать для количественной оценки связи между двумя переменными.

Мы можем использовать функцию OLS() из пакета statsmodels, чтобы быстро подобрать простую модель линейной регрессии для изученных часов и полученных результатов экзамена:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

Подобранное уравнение регрессии имеет вид:

Оценка за экзамен = 69,0734 + 3,8471*(учебные часы)

Это говорит нам о том, что каждый дополнительный час обучения связан со средним увеличением экзаменационной оценки на 3,8471 .

Мы также можем использовать подобранное уравнение регрессии, чтобы спрогнозировать оценку, которую получит студент, исходя из общего количества изученных часов.

Например, студент, который учится 3 часа, должен получить балл 81,6147 :

• Оценка за экзамен = 69,0734 + 3,8471*(учебные часы)
• Оценка экзамена = 69,0734 + 3,8471*(3)
• Результат экзамена = 81,6147

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию о двумерном анализе:

Введение в двумерный анализ
5 примеров двумерных данных в реальной жизни
Введение в простую линейную регрессию
Введение в коэффициент корреляции Пирсона