Как выполнить двумерный анализ в r (с примерами)

Термин двумерный анализ относится к анализу двух переменных. Вы можете это запомнить, потому что приставка «би» означает «два».

Цель двумерного анализа — понять взаимосвязь между двумя переменными.

Существует три распространенных способа выполнения двумерного анализа:

1. Облака точек

2. Коэффициенты корреляции

3. Простая линейная регрессия

В следующем примере показано, как выполнить каждый из этих типов двумерного анализа, используя следующий набор данных, содержащий информацию о двух переменных: (1) часы, потраченные на обучение, и (2) результаты тестов, полученные 20 разными студентами:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Облака точек

Мы можем использовать следующий синтаксис, чтобы создать диаграмму рассеяния количества изученных часов в зависимости от оценки за экзамен в R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

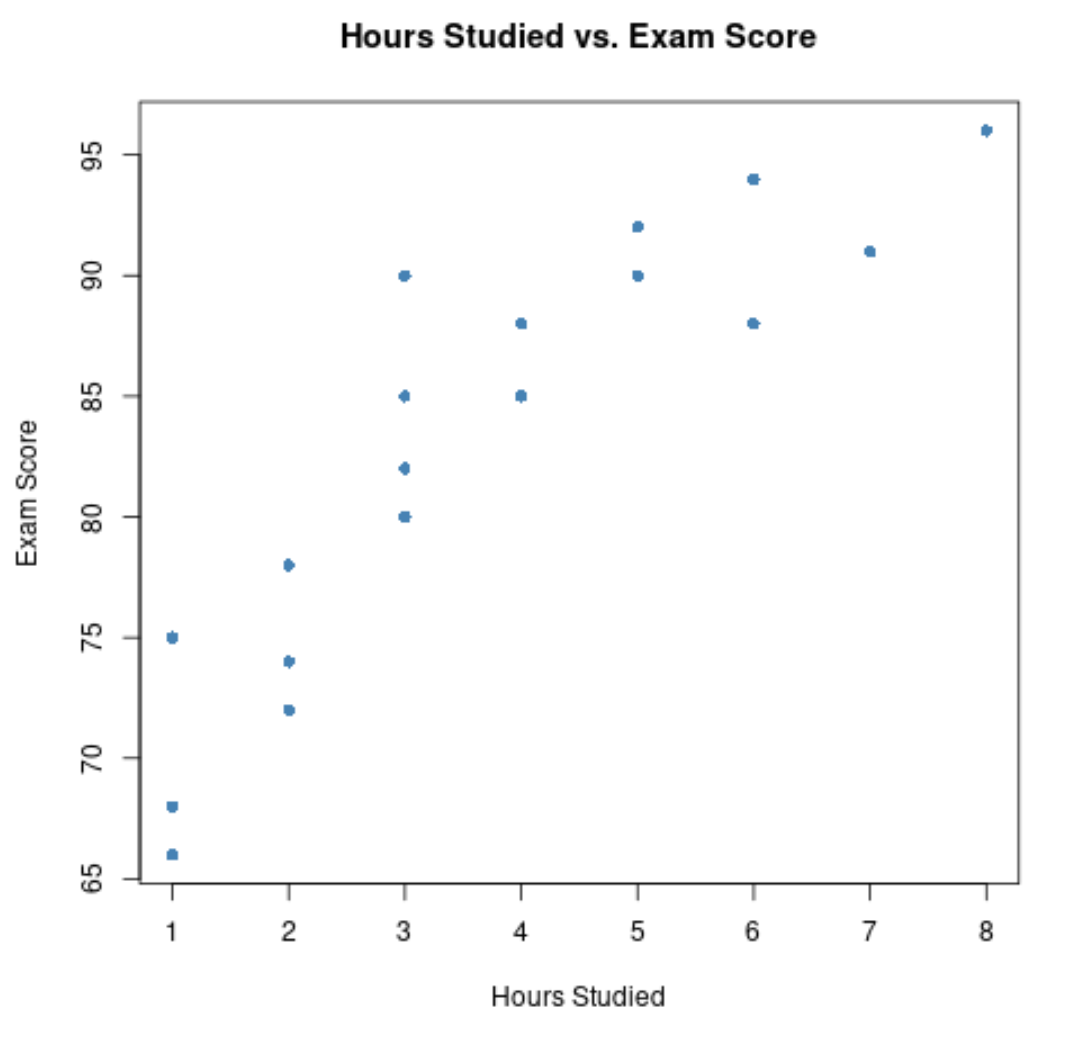
По оси X показано количество учебных часов, а по оси Y — оценка, полученная на экзамене.

График показывает, что между двумя переменными существует положительная связь: по мере увеличения количества учебных часов результаты экзаменов также имеют тенденцию к увеличению.

2. Коэффициенты корреляции

Коэффициент корреляции Пирсона — это способ количественной оценки линейной зависимости между двумя переменными.

Мы можем использовать функцию cor() в R для расчета коэффициента корреляции Пирсона между двумя переменными:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Коэффициент корреляции оказывается равным 0,891 .

Это значение близко к 1, что указывает на сильную положительную корреляцию между количеством учебных часов и оценкой на экзамене.

3. Простая линейная регрессия

Простая линейная регрессия — это статистический метод, который мы можем использовать, чтобы найти уравнение линии, которое лучше всего «соответствует» набору данных, которое мы затем можем использовать, чтобы понять точную взаимосвязь между двумя переменными.

Мы можем использовать функцию lm() в R, чтобы подогнать простую модель линейной регрессии к изученным часам и полученным результатам экзамена:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

Подобранное уравнение регрессии имеет вид:

Оценка за экзамен = 69,0734 + 3,8471*(учебные часы)

Это говорит нам о том, что каждый дополнительный час обучения связан со средним увеличением экзаменационной оценки на 3,8471 .

Мы также можем использовать подобранное уравнение регрессии, чтобы спрогнозировать оценку, которую получит студент, исходя из общего количества изученных часов.

Например, студент, который учится 3 часа, должен получить балл 81,6147 :

• Оценка за экзамен = 69,0734 + 3,8471*(учебные часы)
• Оценка экзамена = 69,0734 + 3,8471*(3)
• Результат экзамена = 81,6147

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию о двумерном анализе:

Введение в двумерный анализ
5 примеров двумерных данных в реальной жизни
Введение в простую линейную регрессию