Как вручную выполнить двусторонний дисперсионный анализ

Двусторонний дисперсионный анализ используется для определения того, существует ли статистически значимая разница между средними значениями трех или более независимых групп, которые были разделены по двум факторам.

В этом руководстве объясняется, как вручную выполнить двусторонний дисперсионный анализ.

Пример: ручной двуфакторный дисперсионный анализ.

Предположим, ботаник хочет знать, влияют ли на рост растений воздействие солнечного света и частота полива. Она сажает 40 семян и дает им расти в течение месяца при различных условиях солнечного света и частоты полива.

Через месяц она записывает высоту каждого растения. Результаты показаны ниже:

В таблице выше мы видим, что в каждой комбинации условий выращивалось по пять растений.

Например, пять растений выращивались при ежедневном поливе и без солнечного света, а их высота через два месяца составила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма и 4,4 дюйма:

Мы можем использовать следующие шаги для выполнения двустороннего дисперсионного анализа:

Шаг 1: Рассчитайте сумму квадратов для первого фактора (частоты полива).

Сначала мы рассчитаем общую среднюю высоту 40 растений:

Общий средний балл = (4,8 + 5 + 6,4 + 6,3 +… + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525.

Далее посчитаем среднюю высоту всех растений, поливаемых ежедневно:

Среднесуточное значение = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8)/20 = 5,155

Далее посчитаем среднюю высоту всех растений, которые поливают каждую неделю:

Среднее значение за неделю = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5)/20 = 5,15.

Далее рассчитаем сумму квадратов коэффициента «частота полива» по следующей формуле:

Σn(X _j – X ..) ²

Золото:

• n : размер выборки группы j
• Σ : греческий символ, означающий «сумма».
• X _j : среднее значение группы j
• X .. : великий средний

В нашем примере мы вычисляем сумму квадратов коэффициента «частота полива» следующим образом: 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Шаг 2. Рассчитайте сумму квадратов второго фактора (воздействие солнца).

Сначала мы рассчитаем общую среднюю высоту 40 растений:

Общий средний балл = (4,8 + 5 + 6,4 + 6,3 +… + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525.

Далее посчитаем среднюю высоту всех растений, не подвергающихся воздействию солнца:

Среднее значение без солнца = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07.

Мы повторим этот расчет, чтобы найти среднюю высоту растений, подвергающихся различному солнечному воздействию:

• Среднее количество солнечного света = 5,1.
• Средний средний солнечный свет = 5,89
• Среднее количество яркого солнечного света = 5,55.

Далее мы рассчитаем сумму квадратов коэффициента «солнечного воздействия» по следующей формуле:

Σn(X _j – X ..) ²

Золото:

• n : размер выборки группы j
• Σ : греческий символ, означающий «сумма».
• X _j : среднее значение группы j
• X .. : великий средний

В нашем примере мы вычисляем сумму квадратов фактора «воздействие солнца» следующим образом: 10(4,07-5,1525) ² + 10(5,1-5,1525) ² + 10(5,89-5,1525) ² + 10(5,55-5,1525) ² = 18,76475

Шаг 3: Вычислить сумму квадратов внутри (ошибка)

Далее мы рассчитаем сумму квадратов, взяв сумму квадратов разностей между каждой комбинацией факторов и высотой отдельных растений.

Например, средняя высота всех растений, ежедневно поливаемых без воздействия солнечного света, составляет 4,14. Затем мы можем вычислить сумму квадратов разностей для каждого из этих отдельных растений следующим образом:

• СС для ежедневного полива и без солнца: (4,8-4,14) ²⁺ (4,4-4,14) ²⁺ (3,2-4,14) ²⁺ (3,9-4,14) ²⁺ (4,4-4,14) ² = 1,512

Мы можем повторить этот процесс для каждой комбинации факторов:

• SS для ежедневного полива и слабого солнечного света: 0,928.
• SS при ежедневном поливе и среднем солнечном свете: 1788.
• СС для ежедневного полива и сильного солнечного света: 1,648.
• СС для еженедельного полива без солнца: 0,34.
• SS для еженедельного полива и слабого солнечного света: 0,548.
• SS для еженедельного полива и среднего солнечного света: 0,652.
• СС для еженедельного полива и сильного солнечного света: 1268.

Затем мы можем взять сумму всех этих значений, чтобы найти сумму квадратов внутри (ошибка):

Суммы квадратов в пределах = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684.

Шаг 4. Подсчитайте общую сумму квадратов.

Затем мы можем вычислить общую сумму квадратов, взяв сумму разностей между высотой каждого растения и средним значением:

Общая сумма квадратов = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Шаг 5: Рассчитайте сумму квадратов взаимодействия

Далее мы рассчитаем сумму взаимодействия квадратов по следующей формуле:

• Взаимодействие SS = Всего SS – Фактор SS 1 – Фактор SS 2 – Внутренняя часть SS
• Взаимодействие СС = 28,45975 – 0,00025 – 18,76475 – 8,684
• Взаимодействие СС = 1,01075

Шаг 6. Заполните таблицу ANOVA.

Наконец, мы заполним значения из двусторонней таблицы ANOVA:

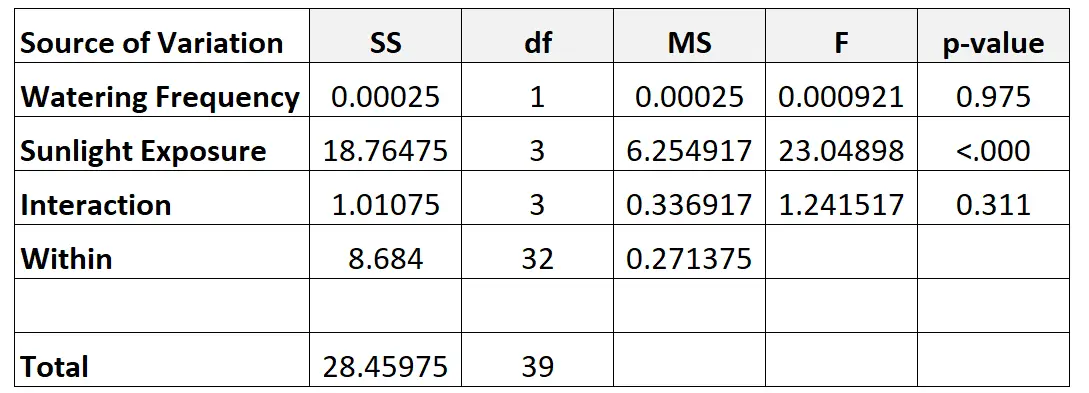
Вот как мы рассчитали разные числа в таблице:

• df Частота полива: d-1 = 2-1 = 1
• df Воздействие солнца: k-1 = 4-1 = 3
• dfInteraction : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• общая df: n-1 = 40-1 = 39
• МС: СС/ДФ
• Частота полива F : частота полива MS/MS в помещении.
• F Воздействие солнечного света : MS/MS воздействие солнечного света в помещении
• Взаимодействие F : Взаимодействие MS/MS внутри
• Частота полива с значением p : значение p, которое соответствует значению F 0,000921 с числителем df = 1 и знаменателем df = 32.
• Значение p воздействия солнца : значение p, которое соответствует значению F 23,04898 с числителем df = 3 и знаменателем df = 32.
• Взаимодействие p-значения : значение p, соответствующее значению F 1,241517 с числителем df = 3 и знаменателем df = 32.

Примечание №1: n = общее количество наблюдений, j = количество уровней частоты полива, k = количество уровней воздействия солнца.

Примечание №2 : Значения p, соответствующие значению F, были рассчитаны с использованием калькулятора F-распределения.

Шаг 7: Интерпретируйте результаты

Из таблицы ANOVA мы можем наблюдать следующее:

• Значение p для взаимодействия между частотой полива и пребыванием на солнце составило 0,311 . Это не является статистически значимым при α = 0,05.
• Значение p для частоты полива составило 0,975 . Это не является статистически значимым при α = 0,05.
• Значение p для пребывания на солнце составляло <0,000 . Это статистически значимо при α = 0,05.

Эти результаты показывают, что воздействие солнца является единственным фактором, статистически значимо влияющим на высоту растений.

А поскольку эффекта взаимодействия нет, эффект воздействия солнца одинаков на каждом уровне частоты полива.

Проще говоря, то, поливают ли растение ежедневно или еженедельно, не влияет на то, как солнце влияет на растение.

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию о ANOVA:

Как вручную выполнить однофакторный дисперсионный анализ
Как вручную выполнить повторные измерения ANOVA
Полное руководство: Как сообщить о результатах двустороннего дисперсионного анализа