Введение в деревья классификации и регрессии
Когда взаимосвязь между набором переменных-предикторов и переменной отклика является линейной, такие методы, как множественная линейная регрессия, могут создавать точные прогностические модели.
Однако, когда взаимосвязь между набором предикторов и ответом сильно нелинейна и сложна, нелинейные методы могут работать лучше.
Примером нелинейного метода являются деревья классификации и регрессии , часто сокращенно CART .
Как следует из названия, модели CART используют набор переменных-предсказателей для создания деревьев решений , которые прогнозируют значение переменной ответа.
Например, предположим, что у нас есть набор данных, содержащий переменные-предсказатели « Сыгранные годы » и «Средние хоум-раны» , а также переменную ответа « Годовая зарплата» для сотен профессиональных бейсболистов.
Вот как может выглядеть дерево регрессии для этого набора данных:
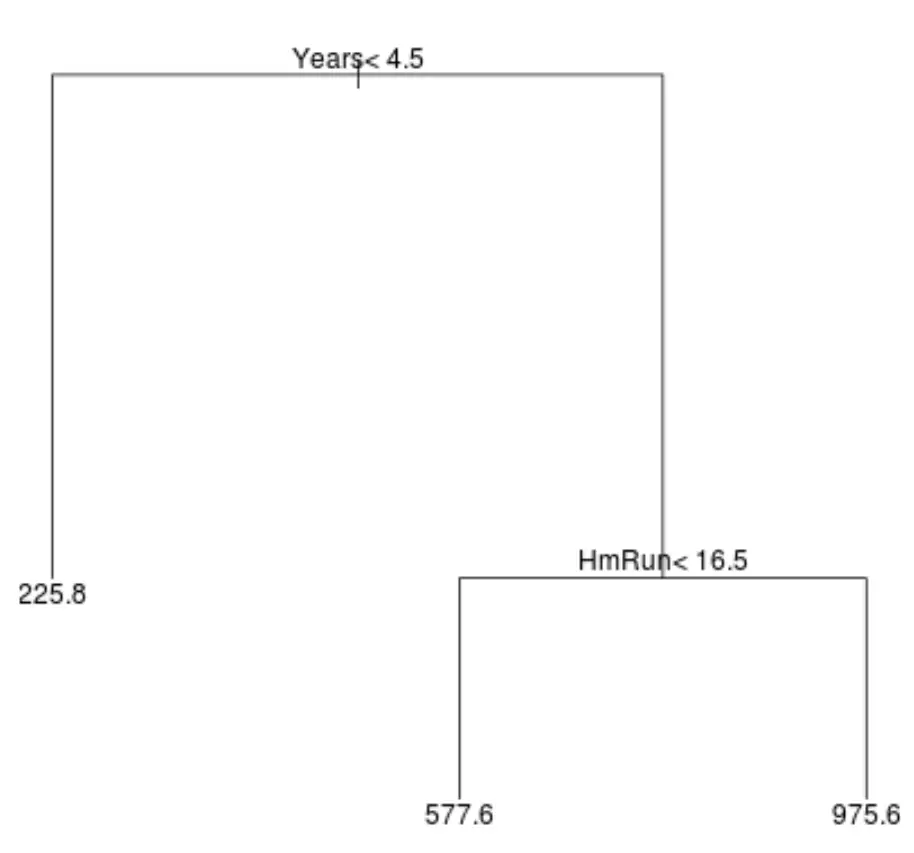
Способ интерпретации дерева следующий:
- Прогнозируемая зарплата игроков, играющих менее 4,5 лет, составит 225,8 тысяч долларов.
- Игроки, которые играли более 4,5 лет и более и совершали менее 16,5 хоум-ранов, в среднем имеют прогнозируемую зарплату в размере 577,6 тысяч долларов.
- Игроки с игровым опытом 4,5 и более лет и в среднем 16,5 хоум-ранов и более имеют ожидаемую зарплату в размере 975,6 тысяч долларов.
Результаты этой модели должны интуитивно иметь смысл: игроки с большим опытом и более средними хоум-ранами, как правило, получают более высокие зарплаты.
Затем мы можем использовать эту модель для прогнозирования зарплаты нового игрока.
Например, предположим, что данный игрок играл 8 лет и в среднем совершал 10 хоумранов в год. Согласно нашей модели, мы прогнозируем, что годовая зарплата этого игрока составит 577,6 тысяч долларов.
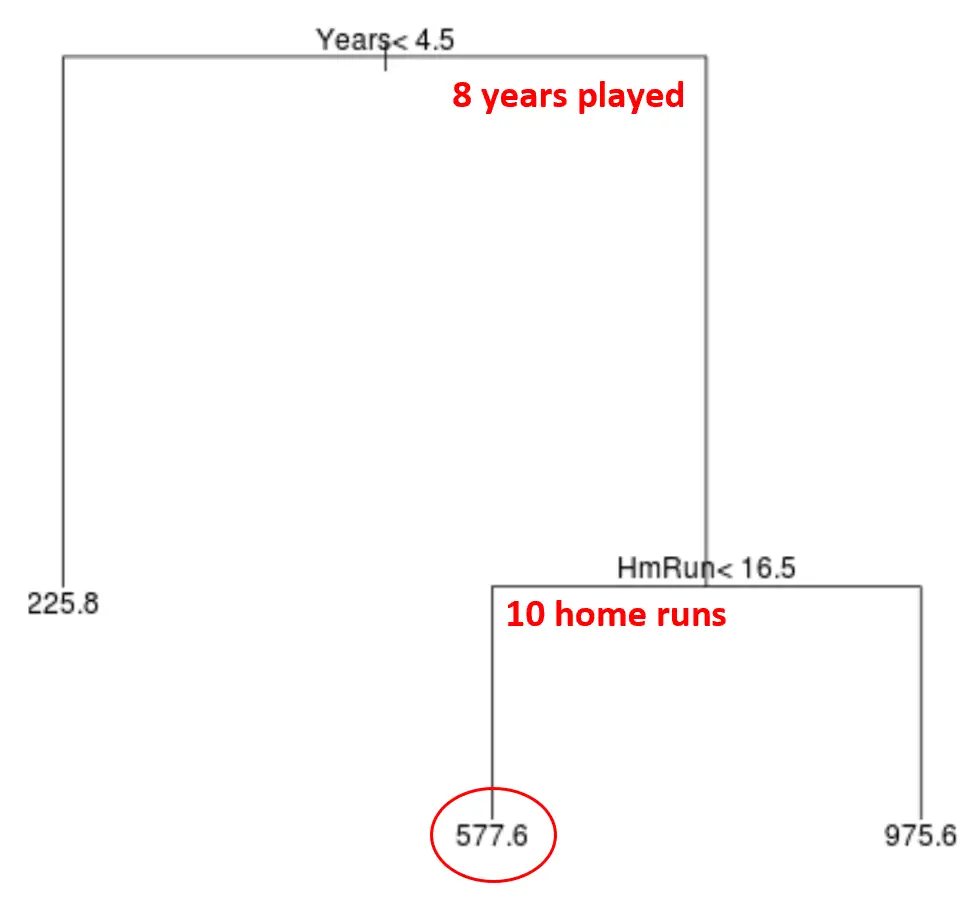
Несколько замечаний по дереву:
- Первая прогнозируемая переменная, расположенная наверху дерева, является наиболее важной, то есть той, которая больше всего влияет на прогноз значения переменной отклика. В этом случае сыгранные годы предсказывают зарплату лучше, чем средний показатель по трассам .
- Области в нижней части дерева называются листовыми узлами . Это конкретное дерево имеет три конечных узла.
Шаги по созданию моделей CART
Мы можем использовать следующие шаги для создания модели CART для данного набора данных:
Шаг 1. Используйте рекурсивное двоичное разбиение, чтобы вырастить большое дерево на основе обучающих данных.
Во-первых, мы используем жадный алгоритм, называемый рекурсивным двоичным разделением, для выращивания дерева регрессии, используя следующий метод:
- Считайте, что все переменные-предикторы X 1 , X 2 , … , остаточная стандартная ошибка) являются наименьшими. .
- Для деревьев классификации мы выбираем предиктор и точку отсечения так, чтобы полученное дерево имело наименьший уровень ошибок классификации.
- Повторите этот процесс, останавливаясь только тогда, когда каждый конечный узел имеет меньше определенного минимального количества наблюдений.
Этот алгоритм является жадным , поскольку на каждом этапе процесса построения дерева он определяет наилучшее разбиение, основываясь только на этом шаге, вместо того, чтобы заглядывать в будущее и выбирать разбиение, которое приведет к лучшему глобальному дереву на будущем этапе.
Шаг 2. Примените сокращение сложности стоимости к большому дереву, чтобы получить последовательность лучших деревьев на основе α.
После того, как мы вырастили большое дерево, нам нужно его обрезать , используя метод, известный как комплексная обрезка, который работает следующим образом:
- Для каждого возможного дерева с T терминальными узлами найдите дерево, которое минимизирует RSS + α|T|.
- Обратите внимание: когда мы увеличиваем значение α, штрафуются деревья с большим количеством конечных узлов. Это гарантирует, что дерево не станет слишком сложным.
В результате этого процесса получается последовательность лучших деревьев для каждого значения α.
Шаг 3: Используйте k-кратную перекрестную проверку, чтобы выбрать α.
Как только мы найдем лучшее дерево для каждого значения α, мы сможем применить k-кратную перекрестную проверку , чтобы выбрать значение α, которое минимизирует ошибку тестирования.
Шаг 4: Выберите окончательный шаблон.
Наконец, мы выбираем окончательную модель как ту, которая соответствует выбранному значению α.
Преимущества и недостатки моделей CART
Модели CART обладают следующими преимуществами :
- Их легко интерпретировать.
- Их легко объяснить.
- Их легко визуализировать.
- Их можно применять как к задачам регрессии, так и к задачам классификации .
Однако модели CART имеют следующие недостатки:
- Они, как правило, не имеют такой точности прогнозирования, как другие алгоритмы нелинейного машинного обучения. Однако за счет кластеризации множества деревьев решений с помощью таких методов, как пакетирование, повышение и случайный лес, можно повысить точность их прогнозирования.
Связанный: Как подогнать деревья классификации и регрессии в R