Как подогнать деревья классификации и регрессии в r

Когда связь между набором переменных-предикторов и переменной отклика является линейной, такие методы, как множественная линейная регрессия, могут создавать точные прогностические модели.

Однако когда взаимосвязь между набором предикторов и ответом более сложна, нелинейные методы часто могут создавать более точные модели.

Одним из таких методов является дерево классификации и регрессии (CART), которое использует набор переменных-предикторов для создания деревьев решений, прогнозирующих значение переменной ответа.

Если переменная ответа является непрерывной, мы можем построить деревья регрессии, а если переменная ответа является категориальной, мы можем построить деревья классификации.

В этом руководстве объясняется, как создавать деревья регрессии и классификации в R.

Пример 1. Построение дерева регрессии в R

В этом примере мы будем использовать набор данных Hitters из пакета ISLR , который содержит различную информацию о 263 профессиональных бейсболистах.

Мы будем использовать этот набор данных для построения дерева регрессии, которое использует переменные-предсказатели хоум-ранов и сыгранных лет для прогнозирования зарплаты данного игрока.

Используйте следующие шаги, чтобы создать это дерево регрессии.

Шаг 1: Загрузите необходимые пакеты.

Сначала мы загрузим необходимые пакеты для этого примера:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Шаг 2. Постройте исходное дерево регрессии.

Сначала мы построим большое исходное дерево регрессии. Мы можем гарантировать, что дерево большое, используя небольшое значение для cp , что означает «параметр сложности».

Это означает, что мы будем выполнять дальнейшее разбиение дерева регрессии до тех пор, пока общий R-квадрат модели увеличится как минимум на значение, указанное cp.

Затем мы воспользуемся функцией printcp() для печати результатов модели:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Шаг 3: Обрежьте дерево.

Далее мы сократим дерево регрессии, чтобы найти оптимальное значение для cp (параметра сложности), которое приводит к наименьшей ошибке теста.

Обратите внимание, что оптимальным значением cp является то, которое приводит к наименьшей x-ошибке в предыдущем выходе, что представляет собой ошибку наблюдений на основе данных перекрестной проверки.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

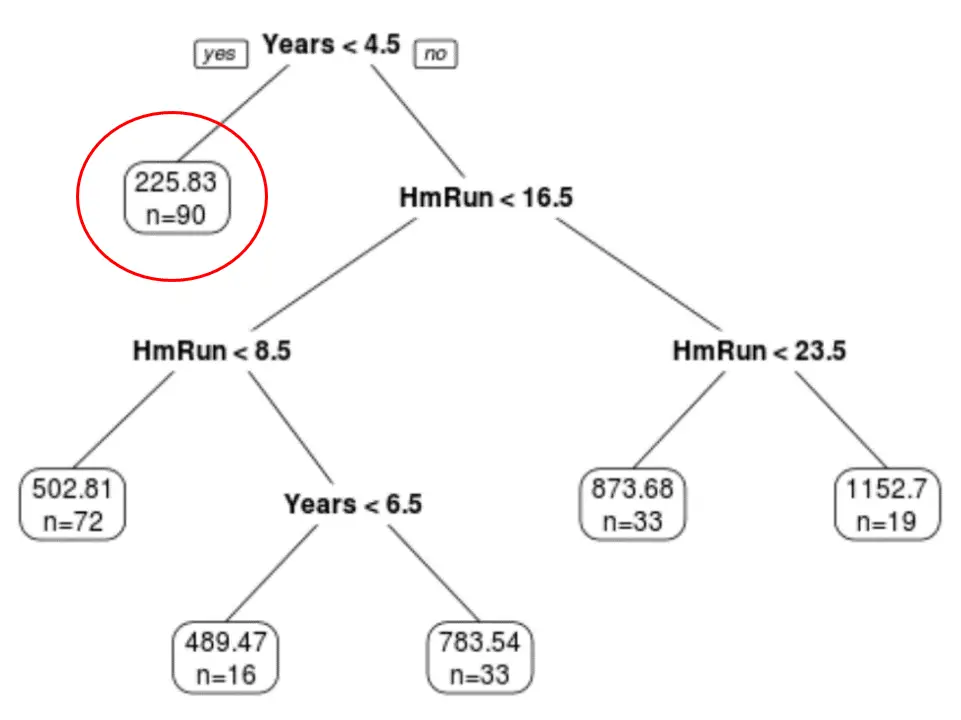
Мы видим, что окончательное обрезанное дерево имеет шесть конечных узлов. Каждый листовой узел отображает прогнозируемую зарплату игроков в этом узле, а также количество наблюдений из исходного набора данных, принадлежащих этому классу.

Например, мы видим, что в исходном наборе данных было 90 игроков со стажем менее 4,5 лет, а их средняя зарплата составляла 225,83 тысячи долларов.

Шаг 4. Используйте дерево для прогнозирования.

Мы можем использовать последнее обрезанное дерево, чтобы спрогнозировать зарплату конкретного игрока, основываясь на его многолетнем опыте и средних хоум-ранах.

Например, игрок, имеющий 7 лет опыта и в среднем 4 хоумрана, имеет ожидаемую зарплату в размере 502,81 тыс. долларов .

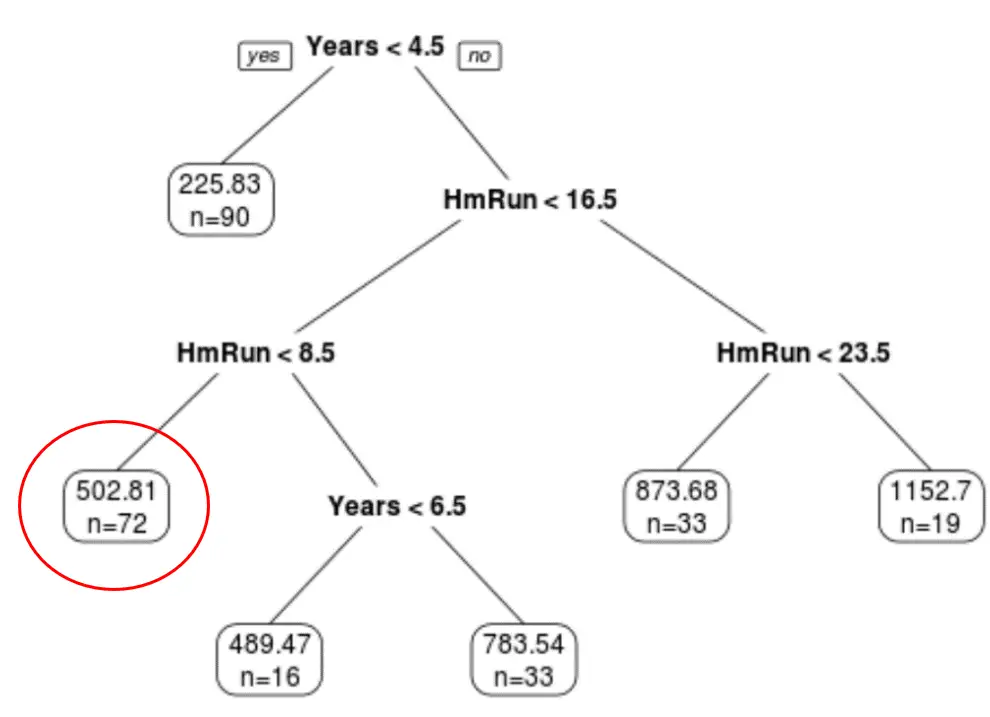
Мы можем использовать функцию Predict() в R, чтобы подтвердить это:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Пример 2. Построение дерева классификации в R

В этом примере мы будем использовать набор данных ptitanic из пакета rpart.plot , который содержит различную информацию о пассажирах на борту Титаника.

Мы будем использовать этот набор данных для создания дерева классификации, которое использует переменные-предикторы class , пол и возраст , чтобы предсказать, выжил ли данный пассажир или нет.

Используйте следующие шаги, чтобы создать это дерево классификации.

Шаг 1: Загрузите необходимые пакеты.

Сначала мы загрузим необходимые пакеты для этого примера:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Шаг 2: Постройте исходное дерево классификации.

Сначала мы построим большое исходное дерево классификации. Мы можем гарантировать, что дерево большое, используя небольшое значение для cp , что означает «параметр сложности».

Это означает, что мы будем выполнять дальнейшее разбиение дерева классификации до тех пор, пока общее соответствие модели увеличится как минимум на значение, указанное cp.

Затем мы воспользуемся функцией printcp() для печати результатов модели:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Шаг 3: Обрежьте дерево.

Далее мы сократим дерево регрессии, чтобы найти оптимальное значение для cp (параметра сложности), которое приводит к наименьшей ошибке теста.

Обратите внимание, что оптимальным значением cp является то, которое приводит к наименьшей x-ошибке в предыдущем выходе, что представляет собой ошибку наблюдений на основе данных перекрестной проверки.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

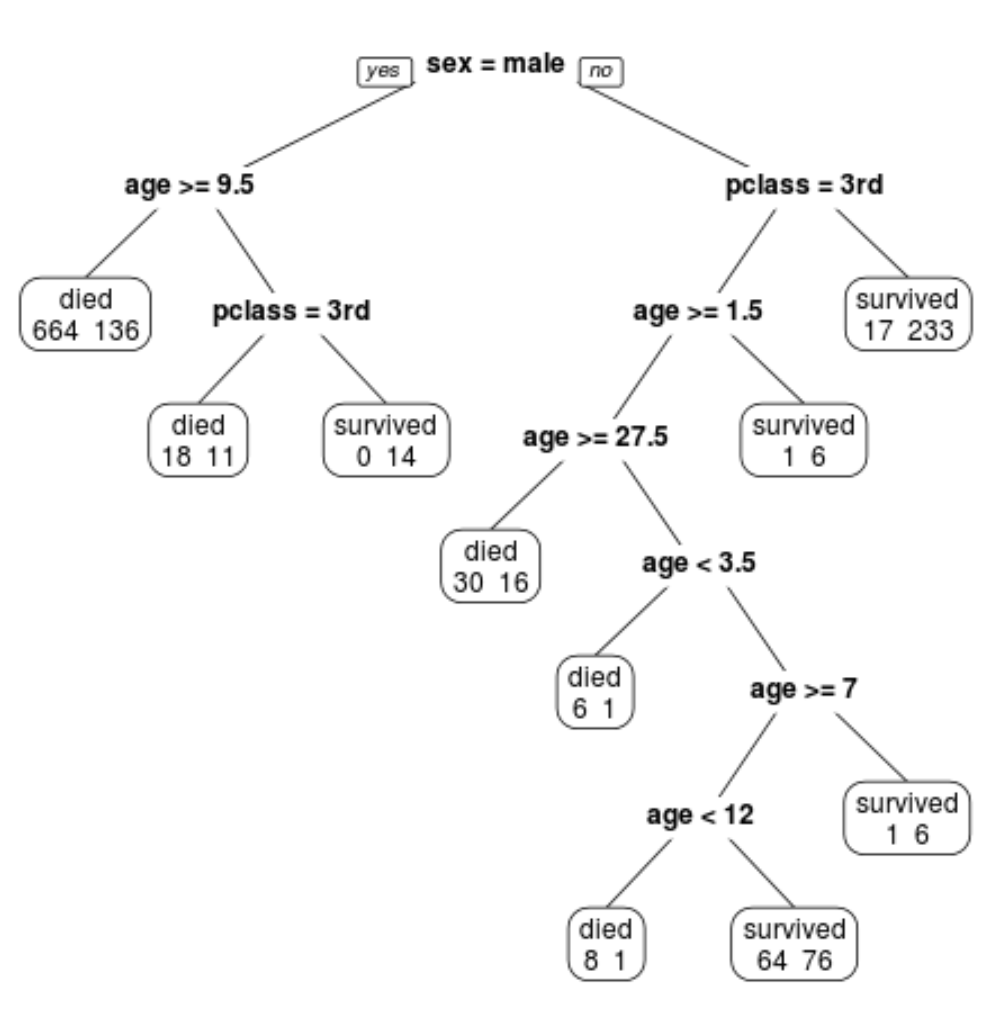
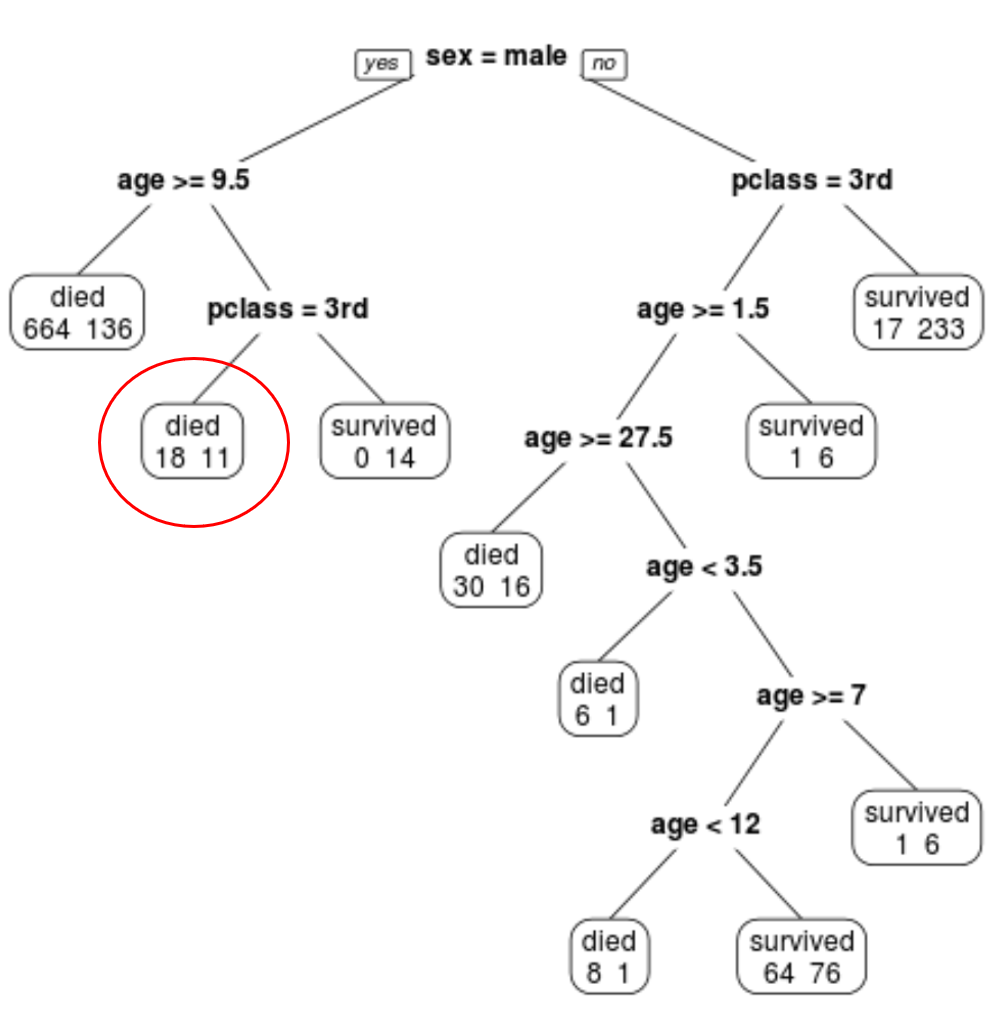
Мы видим, что окончательное обрезанное дерево имеет 10 конечных узлов. На каждом конечном узле указано количество погибших пассажиров, а также количество выживших.

Например, в крайнем левом узле мы видим, что 664 пассажира погибли и 136 выжили.

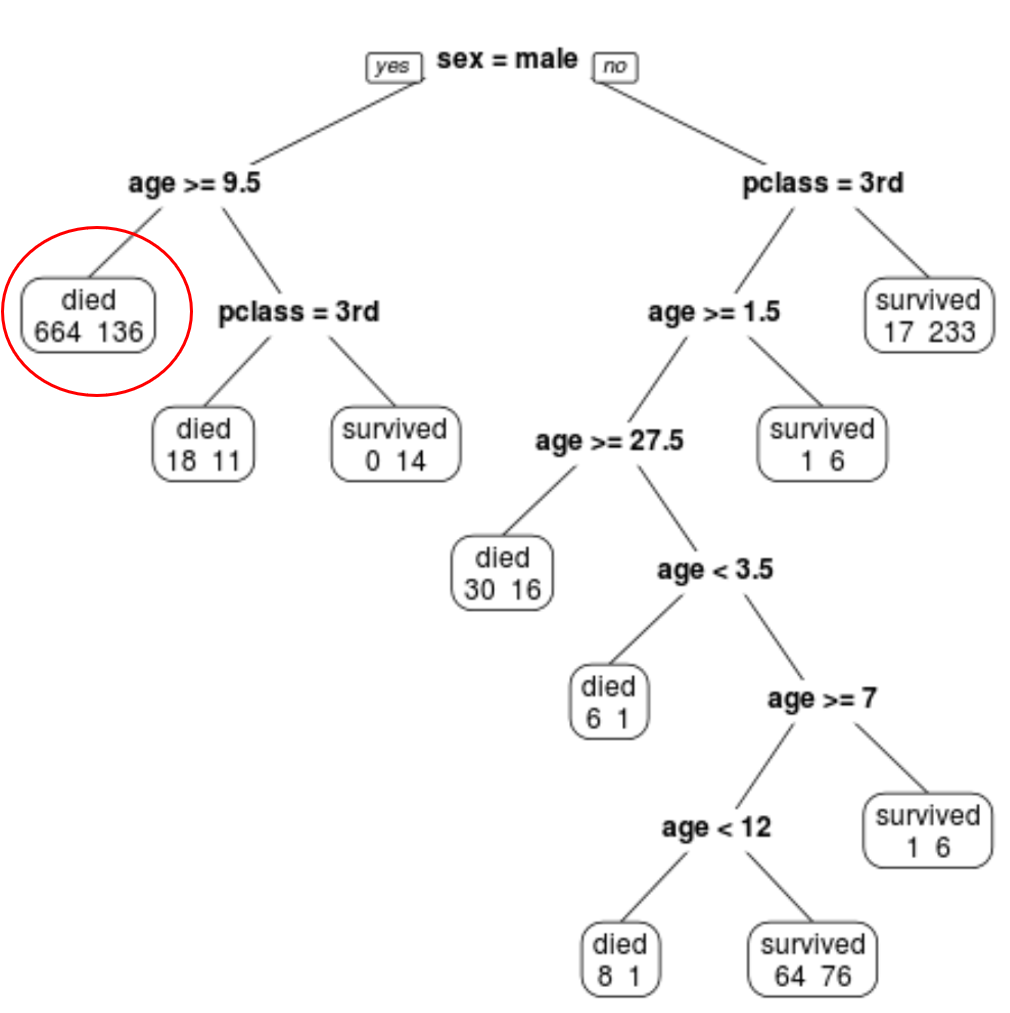
Шаг 4. Используйте дерево для прогнозирования.

Мы можем использовать окончательное обрезанное дерево, чтобы предсказать вероятность выживания конкретного пассажира в зависимости от его класса, возраста и пола.

Например, для пассажира мужского пола в возрасте 8 лет, учащегося в 1-м классе, вероятность выживания составляет 11/29 = 37,9%.

Полный код R, использованный в этих примерах, вы можете найти здесь .