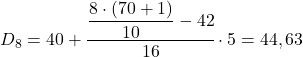Децили
В этой статье мы объясним, что такое децили и как они рассчитываются. Вы также найдете несколько решенных пошаговых примеров расчета децилей и, кроме того, сможете посчитать децили любой статистической выборки с помощью онлайн-калькулятора.
Что такое децили?
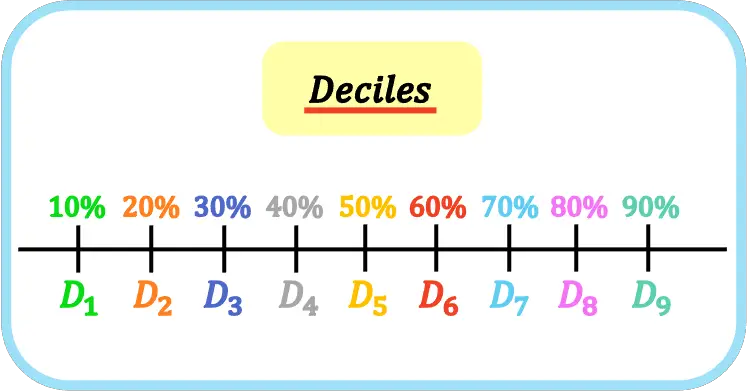
В статистике децили — это девять величин, которые делят набор упорядоченных данных на десять равных частей. Таким образом, первый, второй, третий… дециль представляет 10%, 20%, 30%… выборки или совокупности.
Например, значение четвертого дециля выше 40% данных, но ниже остальных данных.
Децили обозначаются заглавной буквой Д и децильным индексом, то есть первый дециль — Д 1 , второй дециль — Д 2 , третий дециль — Д 3 и т. д.
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать децили для любого набора данных.
Следует отметить, что децили являются мерой нецентрального положения так же, как квартили, квинтили и процентили. Вы можете проверить значение каждого из этих типов квантилей на нашем сайте.
Кроме того, пятый дециль эквивалентен медиане и второму квартилю, поскольку они делят весь набор данных на две равные части.
Как посчитать децили
Чтобы вычислить децильную позицию ряда статистических данных, умножьте число децилей на сумму общего количества данных плюс один и разделите результат на десять.
Таким образом, формула дециля имеет вид:
![]()
Обратите внимание: эта формула сообщает нам положение дециля, а не его значение. Децилем будут данные, расположенные в позиции, полученной по формуле.
Однако иногда результат этой формулы дает нам десятичное число, поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:
- Если результатом формулы является число без десятичной части , децилем являются данные, расположенные в позиции, указанной в формуле выше.
- Если результатом формулы является число с десятичной частью , значение дециля рассчитывается по следующей формуле:
![]()
Где x i и x i+1 — номера позиций, между которыми находится число, полученное по первой формуле, а d — десятичная часть числа, полученного по первой формуле.
Вы можете подумать, что получить децили статистической выборки сложно, но на практике это довольно просто. Если вы прочитаете следующие два примера, вы наверняка поймете это гораздо лучше.
Примечание . В научном сообществе нет единого мнения о том, как рассчитывать децили, поэтому вы можете найти книги по статистике, которые объясняют это немного по-другому.
Пример расчета дециля
Как вы видели выше, расчет децилей зависит от того, является ли число, которое дает нам первая формула, десятичным или нет, поэтому ниже мы подготовили два решенных примера, по одному для каждого случая. В любом случае помните, что если у вас есть вопросы по составу децилей, вы можете задать их в комментариях.
Пример 1
- Учитывая следующие данные, от меньшего к большему, найдите первый, третий и восьмой дециль выборки.

Данные в этом упражнении уже отсортированы, поэтому нет необходимости менять порядок, иначе нам пришлось бы сначала сортировать данные от наименьшего к наибольшему.
Как объяснялось выше, формула, позволяющая найти положения децилей, выглядит следующим образом:
![]()
Размер выборки для этого упражнения составляет 29 наблюдений, поэтому для расчета положения первого дециля вы должны заменить n 29 и k 1:
![]()
Результат формулы — 3, поэтому первый дециль будет находиться на третьей позиции упорядоченного списка, и это значение соответствует 85.
Теперь повторим ту же процедуру, но уже с третьим децилем. Мы используем формулу, заменяя k на 3:
![]()
Таким образом, третий дециль будет элементом на девятой позиции, т.е. 97.
Наконец, мы проделываем тот же процесс, но ставим 8 в формулу, чтобы определить восьмой дециль:
![]()
Восьмой дециль будет номером в позиции 24 упорядоченного списка данных, поэтому восьмой дециль равен 131.
Пример 2
- По данным следующей таблицы рассчитайте децили 4, 7 и 9.

Как и в предыдущем примере, для получения позиций децилей необходимо использовать следующую формулу:
![]()
В данном случае размер выборки равен 42, поэтому, чтобы найти положение четвертого дециля, необходимо заменить параметр n на 42, а параметр k на 4:
![]()
Но на этот раз из формулы мы получили десятичное число, поэтому для расчета точного дециля нам нужно применить следующую формулу:
![]()
Число, полученное по первой формуле, равно 17,2, поэтому четвертый дециль находится между семнадцатым и восемнадцатым заданными, что составляет 109 и 112 соответственно. Следовательно, x i равно 109, x i+ 1 равно 112, а d — десятичная часть. полученного числа, т.е. 0,2.
![]()
Мы повторяем тот же процесс, чтобы найти седьмой дециль. Сначала вычисляем положение дециля:
![]()
Из формулы мы получили число 30,1, что означает, что дециль будет находиться между позициями 30 и 31, значения которых равны 154 и 159. Таким образом, расчет точного дециля таков:
![]()
Наконец, мы применяем тот же метод еще раз, чтобы получить девятый дециль. Определяем положение дециля:
![]()
Полученное число является десятичным и находится между 38 и 39, позиции которых соответствуют значениям 189 и 196. Таким образом, расчет дециля 9 выглядит следующим образом:
![]()
Децильный калькулятор
Подключите набор статистических данных к калькулятору ниже, чтобы рассчитать децили. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Децили в сгруппированных данных
Чтобы рассчитать децили, когда данные сгруппированы в интервалы , нам сначала нужно найти интервал или интервал, в который попадает дециль, используя следующую формулу:
![]()
Таким образом, дециль будет находиться в интервале, абсолютная частота которого непосредственно больше числа, полученного в предыдущем выражении.
И как только мы уже знаем интервал, к которому принадлежит дециль, мы должны применить следующую формулу, чтобы найти точное значение дециля:
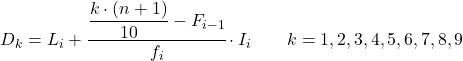
Золото:
- Li – нижняя граница интервала, в котором находится дециль.
- n — общее количество статистических данных.
- F i-1 представляет собой совокупную абсолютную частоту предыдущего интервала.
- f i — абсолютная частота интервала, в котором находится дециль.
- I i – ширина децильного интервала.
Чтобы вы могли увидеть, как это делается, ниже представлено выполненное упражнение, в котором рассчитываются децили 3, 5 и 8 следующих данных, сгруппированных по интервалам.
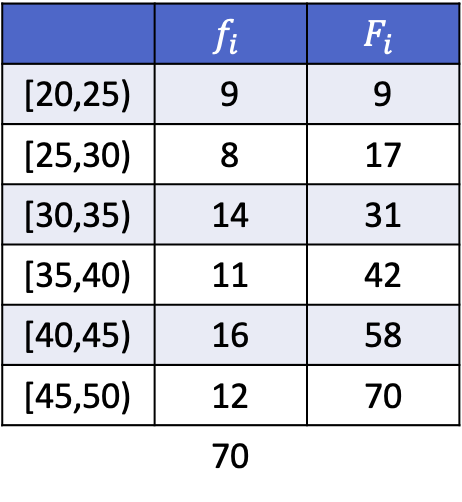
Поскольку данные сгруппированы, расчет каждого дециля состоит из двух этапов: сначала находят интервал, в который попадает дециль, затем вычисляют точное значение дециля. Таким образом, находим интервал третьего дециля:
![]()
![]()
Децильным интервалом будет тот, чья абсолютная кумулятивная частота сразу превышает 21,3, и в данном случае это интервал [30.35), чья абсолютная кумулятивная частота равна 31. Теперь, когда мы знаем децильный интервал, мы применим следующую формулу, чтобы найти точное значение дециля:
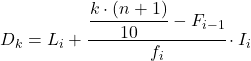
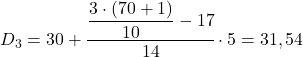
Теперь мы должны повторно применить этот метод, чтобы получить пятый дециль. Сначала определим интервал, в котором он лежит:
![]()
Результат 35 означает, что он находится в интервале [35,40), но не потому, что в выражении интервала есть 35, а потому, что его накопленная абсолютная частота (42) является самой высокой. И как только интервал определен, применяем вторую формулу процесса:
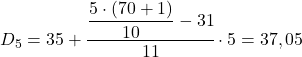
Наконец, находим восьмой дециль. Для этого сначала рассчитаем его интервал:
![]()
Совокупная абсолютная частота непосредственно выше 56,8 равна 58, поэтому диапазон восьмого дециля равен [40,45). Поэтому достаточно определить точное значение дециля: