Может ли дисперсия быть отрицательной?
В статистике термин «дисперсия» относится к тому, как значения распределяются в данном наборе данных.
Обычный вопрос, который студенты задают по поводу дисперсии:
Может ли дисперсия быть отрицательной?
Ответ: Нет, дисперсия не может быть отрицательной. Наименьшее значение, которое оно может принять, равно нулю.
Чтобы понять, почему это так, нам нужно понять, как на самом деле рассчитывается дисперсия.
Как рассчитать зазор
Формула для нахождения дисперсии выборки (обозначенной s 2 ):
s 2 = Σ (x i – x ) 2 / (n-1)
Золото:
- x : Образец означает
- x i : i- е наблюдение в выборке
- N : Размер выборки
- Σ : греческий символ, означающий «сумма».
Например, предположим, что у нас есть следующий набор данных с 10 значениями:
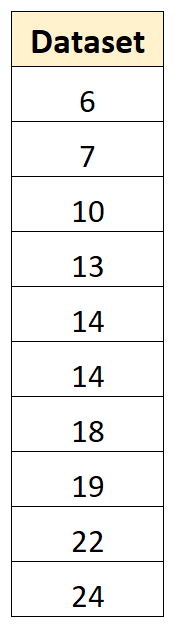
Для расчета дисперсии этой выборки мы можем использовать следующие шаги:
Шаг 1: Найдите среднее значение
Среднее – это просто среднее. Оказывается, это 14,7 .
Шаг 2: Найдите квадраты отклонений
Затем мы можем вычислить квадратическое отклонение каждого отдельного значения от среднего значения.
Например, первое квадратическое отклонение рассчитывается как (6-14,7) 2 = 75,69.
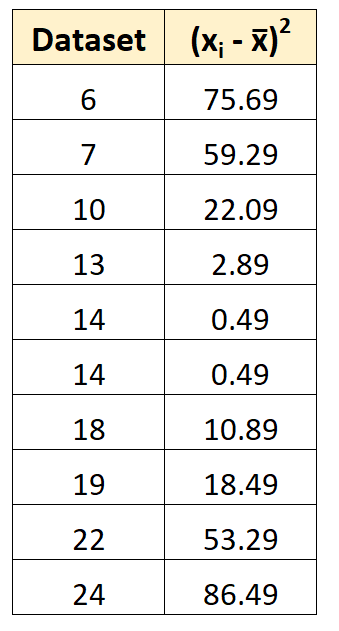
Шаг 3. Найдите сумму квадратов отклонений.
Тогда мы можем просуммировать все квадраты отклонений:
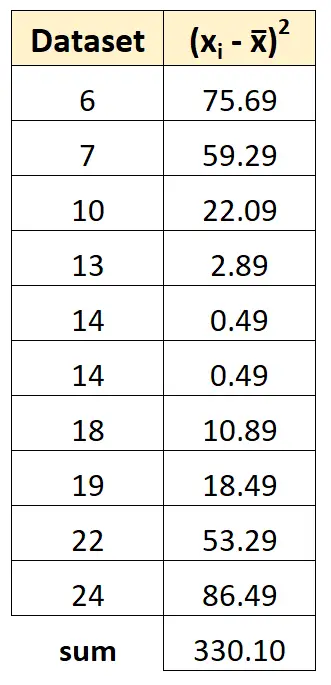
Шаг 4. Рассчитайте выборочную дисперсию
Наконец, мы можем рассчитать выборочную дисперсию как сумму квадратов отклонений, деленную на (n-1):
с 2 = 330,1/(10-1) = 330,1/9 = 36,678
Выборочная дисперсия оказывается равной 36 678 .
Пример нулевой дисперсии
Единственный способ добиться того, чтобы набор данных имел нулевую дисперсию, — это если все значения в наборе данных одинаковы .
Например, следующий набор данных имеет выборочную дисперсию, равную нулю:
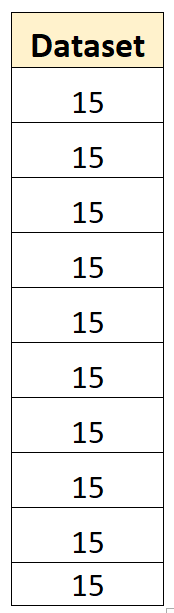
Среднее значение набора данных равно 15, и ни одно из отдельных значений не отличается от среднего. Таким образом, сумма квадратов отклонений будет равна нулю, а выборочная дисперсия будет просто равна нулю.
Может ли стандартное отклонение быть отрицательным?
Более распространенный способ измерения распределения значений в наборе данных — использование стандартного отклонения, которое представляет собой просто квадратный корень из дисперсии.
Например, если дисперсия данной выборки равна s2 = 36,678 , то стандартное отклонение (обозначается s ) рассчитывается следующим образом:
s = √ s2 = √ 36,678 = 6,056
Поскольку мы уже знаем, что дисперсия всегда равна нулю или положительному числу, это означает, что стандартное отклонение никогда не может быть отрицательным, поскольку квадратный корень из нуля или положительного числа не может быть отрицательным.
Дополнительные ресурсы
Меры центральной тенденции: определение и примеры
Меры дисперсии: определение и примеры