Excel: рассчитать доверительный интервал для коэффициента регрессии

В модели линейной регрессии коэффициент регрессии сообщает нам среднее изменение переменной ответа , связанное с увеличением на одну единицу переменной-предиктора.

Мы можем использовать следующую формулу для расчета доверительного интервала для коэффициента регрессии:

Доверительный интервал для β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

Золото:

•   b ₁ = коэффициент регрессии, указанный в таблице регрессии.
• t _{1-∝/2, n-2} = критическое значение t для уровня достоверности 1-∝ с n-2 степенями свободы, где n — общее количество наблюдений в нашем наборе данных.
• se(b ₁ ) = стандартная ошибка b ₁ , показанная в таблице регрессии.

В следующем примере показано, как рассчитать доверительный интервал для коэффициента регрессии в Excel.

Пример: доверительный интервал для коэффициента регрессии в Excel

Предположим, мы хотим подогнать простую модель линейной регрессии, используя часы обучения в качестве предикторной переменной и результаты экзаменов в качестве переменной ответа для 15 учеников в определенном классе:

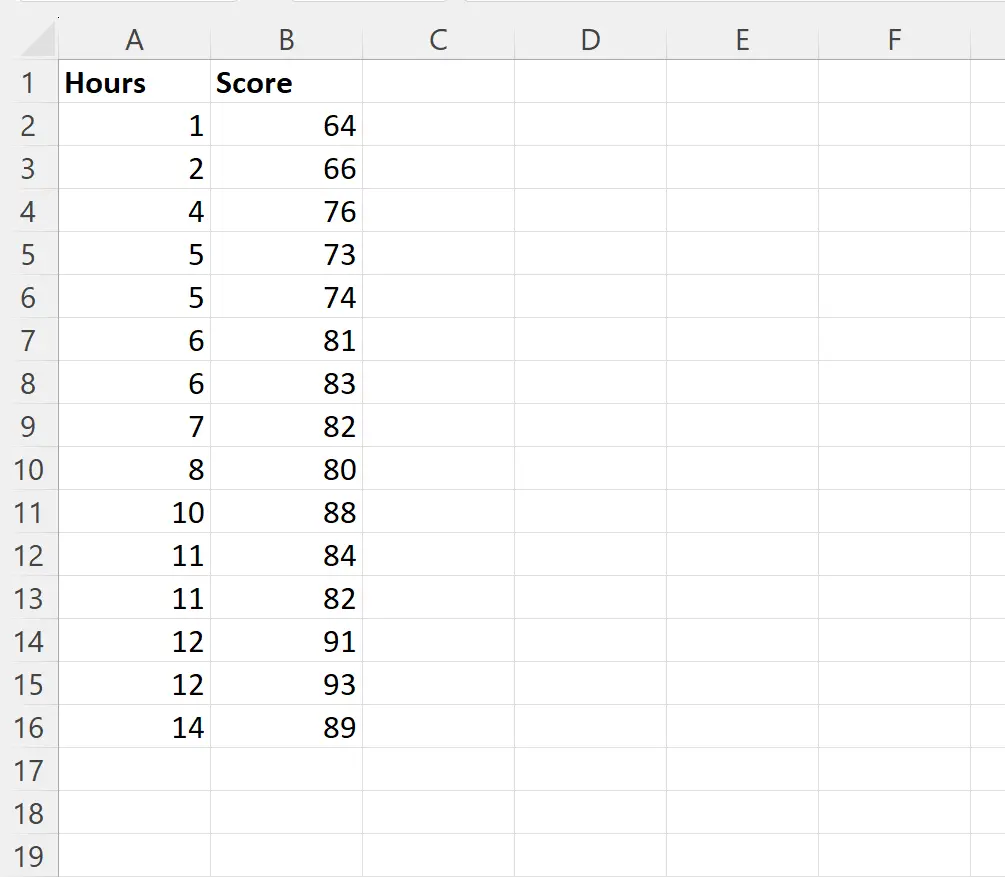
Мы можем ввести следующую формулу в ячейку D2, чтобы выполнить простую линейную регрессию, используя значения в столбце « Часы» в качестве переменной-предиктора, а значения в столбце « Оценка» в качестве переменной ответа:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

Обратите внимание, что первый аргумент TRUE сообщает Excel, что нужно вычислить отрезок уравнения регрессии в обычном режиме, не принуждая его равняться нулю.

Второй аргумент TRUE указывает Excel, что в дополнение к коэффициентам необходимо создать дополнительную статистику регрессии.

На следующем снимке экрана показан результат этой формулы (мы объясняем, что представляет собой каждое выходное значение, в красном тексте под выходными данными):

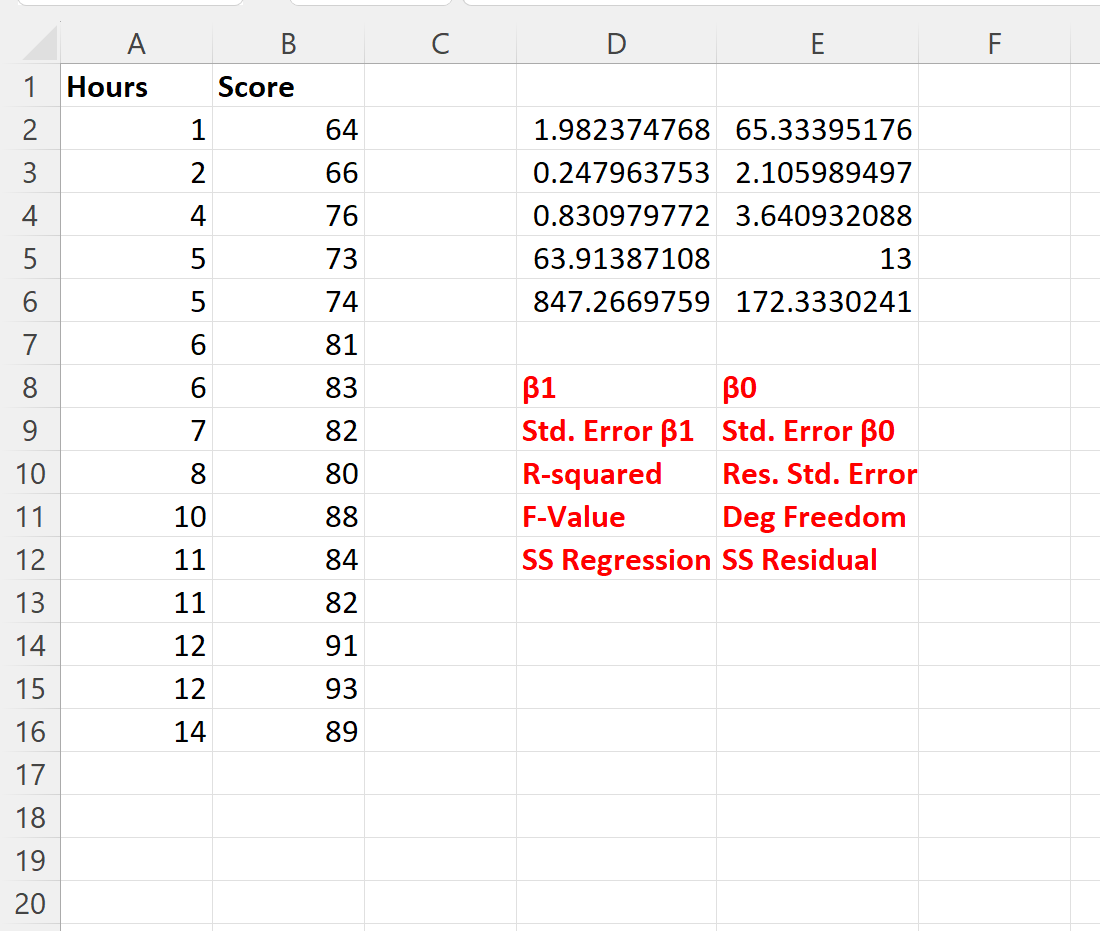
Используя коэффициенты регрессии, мы можем записать подобранное уравнение регрессии следующим образом:

Оценка = 65,334 + 1,982*(Часы обучения)

Обратите внимание, что коэффициент регрессии для часов равен 1,982 .

Это говорит нам о том, что каждый дополнительный час учебного времени связан со средним увеличением экзаменационной оценки на 1982 балла.

Чтобы рассчитать 95% доверительный интервал для коэффициента регрессии, мы можем ввести следующие формулы в ячейки H2 и H3:

• H2: = D2 – T.ОБР.2T(0,05, E5)*D3
• H3: = D2 + T.ОБР.2T(0,05, E5)*D3

На следующем снимке экрана показано, как использовать эти формулы на практике:

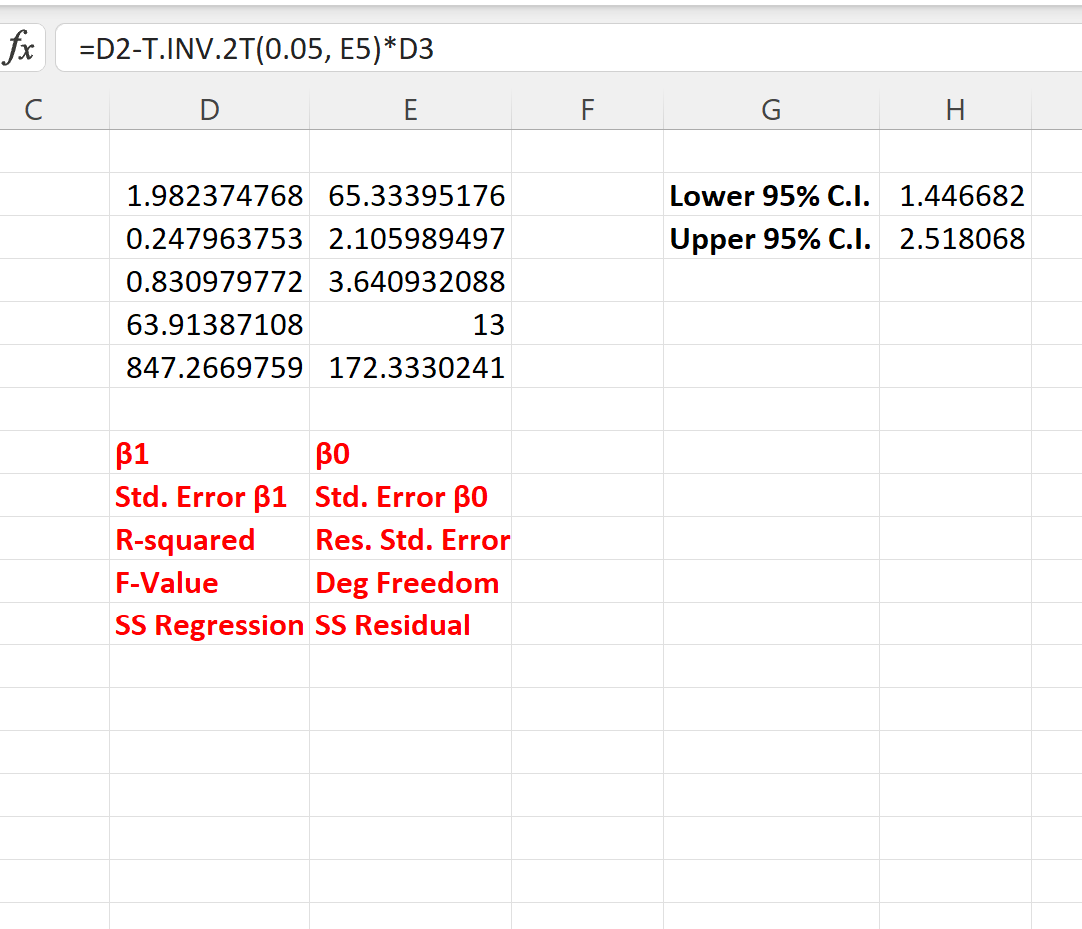
95% доверительный интервал для коэффициента регрессии составляет [1,446, 2,518] .

Поскольку этот доверительный интервал не содержит значения 0 , мы можем заключить, что существует статистически значимая связь между учебными часами и оценкой на экзамене.

Мы также можем подтвердить, что это правильно, вручную рассчитав 95% доверительный интервал для коэффициента регрессии:

• 95% ДИ для β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• 95% ДИ для β ₁ : 1,982 ± t _{0,975, 15-2} * 0,248
• 95% ДИ для β ₁ : 1,982 ± 2,1604 * 0,248
• 95% ДИ для β ₁ : [1,446, 2,518]

95% доверительный интервал для коэффициента регрессии составляет [1,446, 2,518] .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:

Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как интерпретировать значения P в выходных данных регрессии в Excel