Логнормальное распределение
В этой статье объясняется, что такое логнормальное распределение в статистике. Итак, вы узнаете, каковы свойства логнормального распределения и график этого типа распределения вероятностей.
Что такое логнормальное распределение?
Логнормальное распределение или логнормальное распределение — это распределение вероятностей, которое определяет случайную величину, логарифм которой соответствует нормальному распределению.
Следовательно, если переменная X имеет нормальное распределение, то показательная функция ex имеет логнормальное распределение.
Обратите внимание, что логнормальное распределение можно использовать только в том случае, если значения переменных положительны, поскольку логарифм — это функция, принимающая только один положительный аргумент.
Среди различных применений логнормального распределения в статистике мы выделяем использование этого распределения для анализа финансовых вложений и проведения анализа надежности.
Логнормальное распределение также известно как распределение Тинаута , иногда его также называют логнормальным распределением или логнормальным распределением .
График логнормального распределения
Теперь, когда мы знаем определение логнормального распределения, в этом разделе мы увидим, как графическое представление логнормального распределения меняется в зависимости от значений его среднего арифметического и стандартного отклонения.
График функции плотности логнормального распределения выглядит следующим образом:
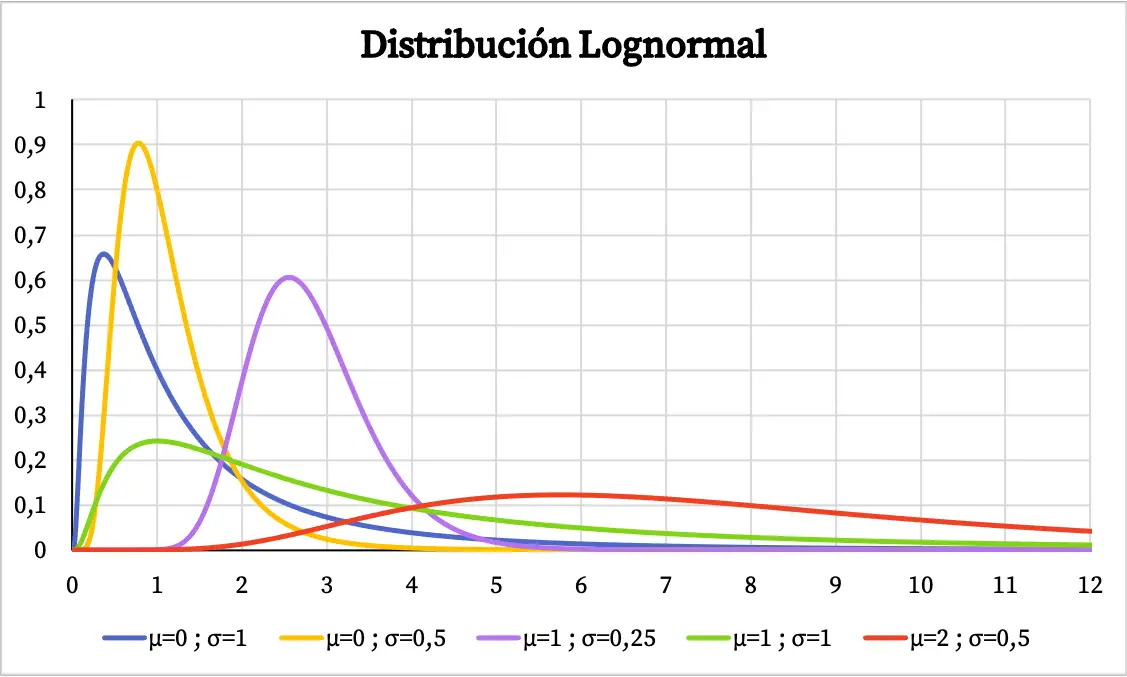
С другой стороны, график кумулятивной вероятности логарифмически нормального распределения выглядит следующим образом:
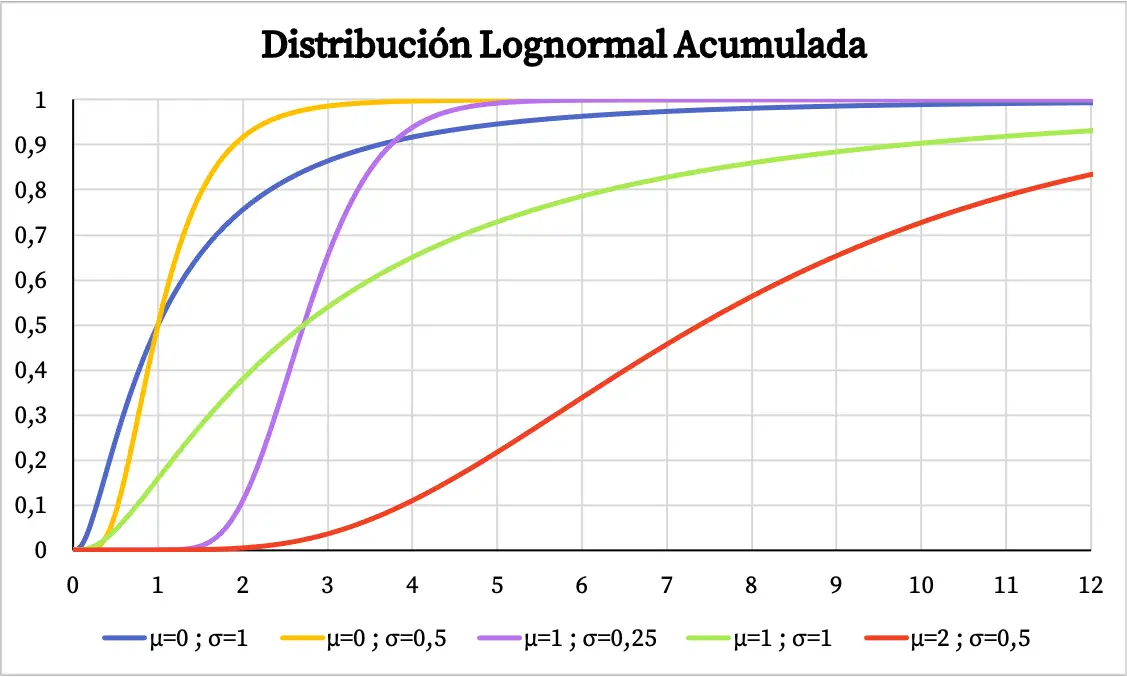
Характеристики логнормального распределения
Логнормальное распределение имеет следующие характеристики:
- Логнормальное распределение определяется значением двух параметров: его среднего арифметического μ и его дисперсии σ 2 .
- Область логнормального распределения состоит из положительных действительных чисел, поскольку логарифм не принимает отрицательные или нулевые значения.
- Ожидание логарифмически нормального распределения равно числу e, возведенному в сумму среднего значения плюс дисперсия, деленная на два.
![\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-109a1024d530b2993db41f1d7a5a24c3_l3.png "Rendered by QuickLaTeX.com")
- С другой стороны, дисперсию логнормального распределения можно рассчитать с помощью следующего выражения:
- Мода логнормального распределения эквивалентна числу e, возведенному в среднее значение распределения.
- Коэффициент асимметрии логнормального распределения можно определить, применив следующую формулу:
- Формула функции плотности логнормального распределения:
![\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-25698732745689402d16ea353a072cc1_l3.png "Rendered by QuickLaTeX.com")
- Формула кумулятивной функции вероятности логнормального распределения:
![\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-59c2474703bad4805a6a44bd05cf92bd_l3.png "Rendered by QuickLaTeX.com")
Золото
— кумулятивная функция вероятности стандартного нормального распределения .
- Среднее арифметическое логнормального распределения больше значения его медианы.
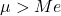
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше