Закон больших чисел: определение + примеры
Закон больших чисел гласит, что по мере увеличения размера выборки среднее значение выборки приближается к ожидаемому значению.
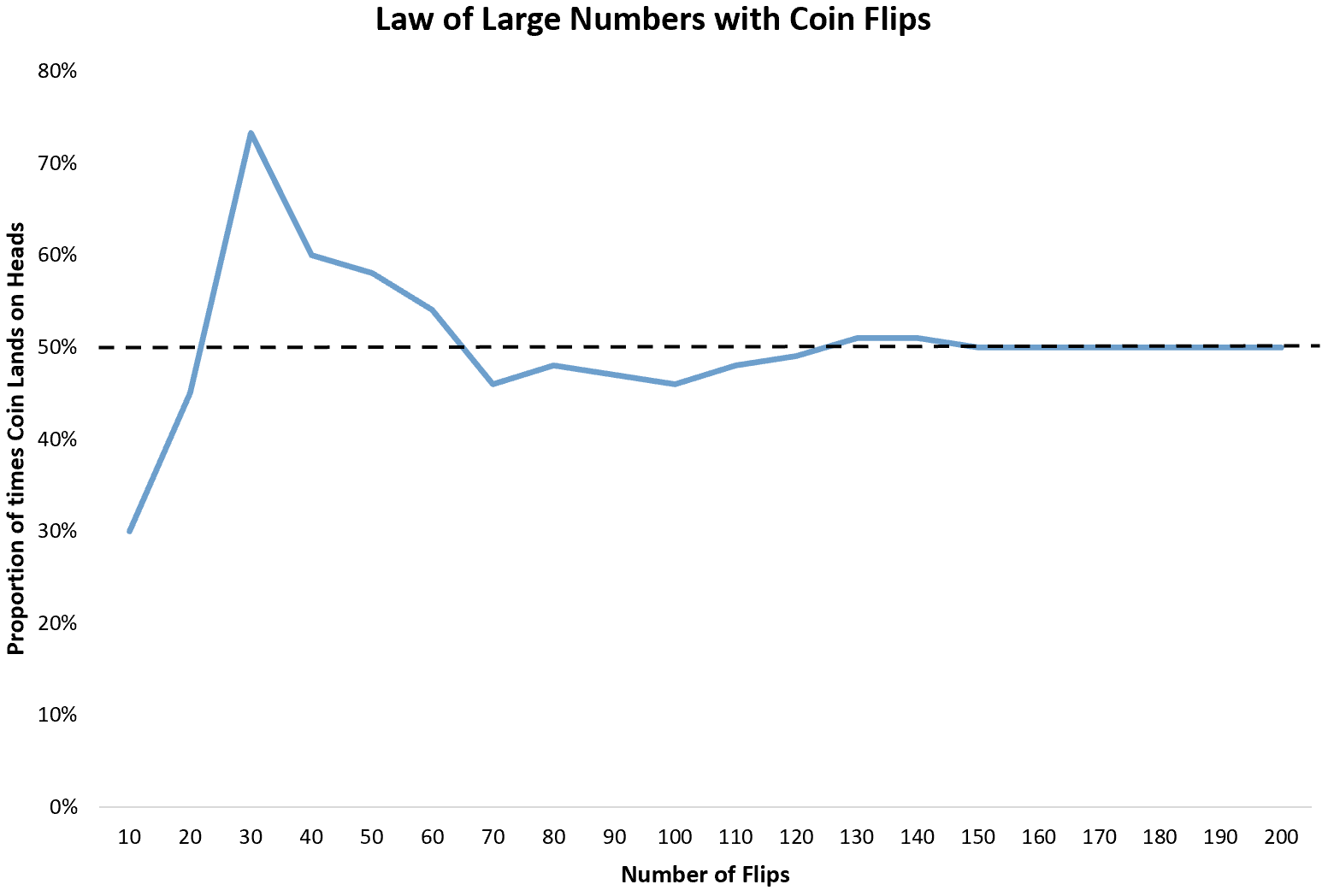
Самый простой пример — подбрасывание монеты. Каждый раз, когда мы подбрасываем монету, вероятность того, что выпадет орел, равна 1/2. Таким образом, ожидаемая доля орлов, которые выпадут при бесконечном количестве бросков, равна 1/2 или 0,5 .
Однако, если мы подбросим монету 10 раз, мы можем обнаружить, что орлом выпадет только 3 раза. Поскольку 10 переворотов — это небольшой размер выборки, нет никакой гарантии, что доля головы будет близка к 0,5 .
Если мы продолжим подбрасывать монету еще 10 раз, мы можем обнаружить, что она упадет орлом в общей сложности 9 раз из 20. Если мы подбросим ее еще 10 раз, мы можем обнаружить, что она выпадет орлом в 22 случаях из 30.
Когда мы подбрасываем монету, доля случаев, когда на ней выпадает орел, будет сходиться к ожидаемой пропорции 0,5 .
Эта простая идея закона больших чисел применяется многими видами бизнеса и отраслей в реальной жизни.
Закон больших чисел в казино
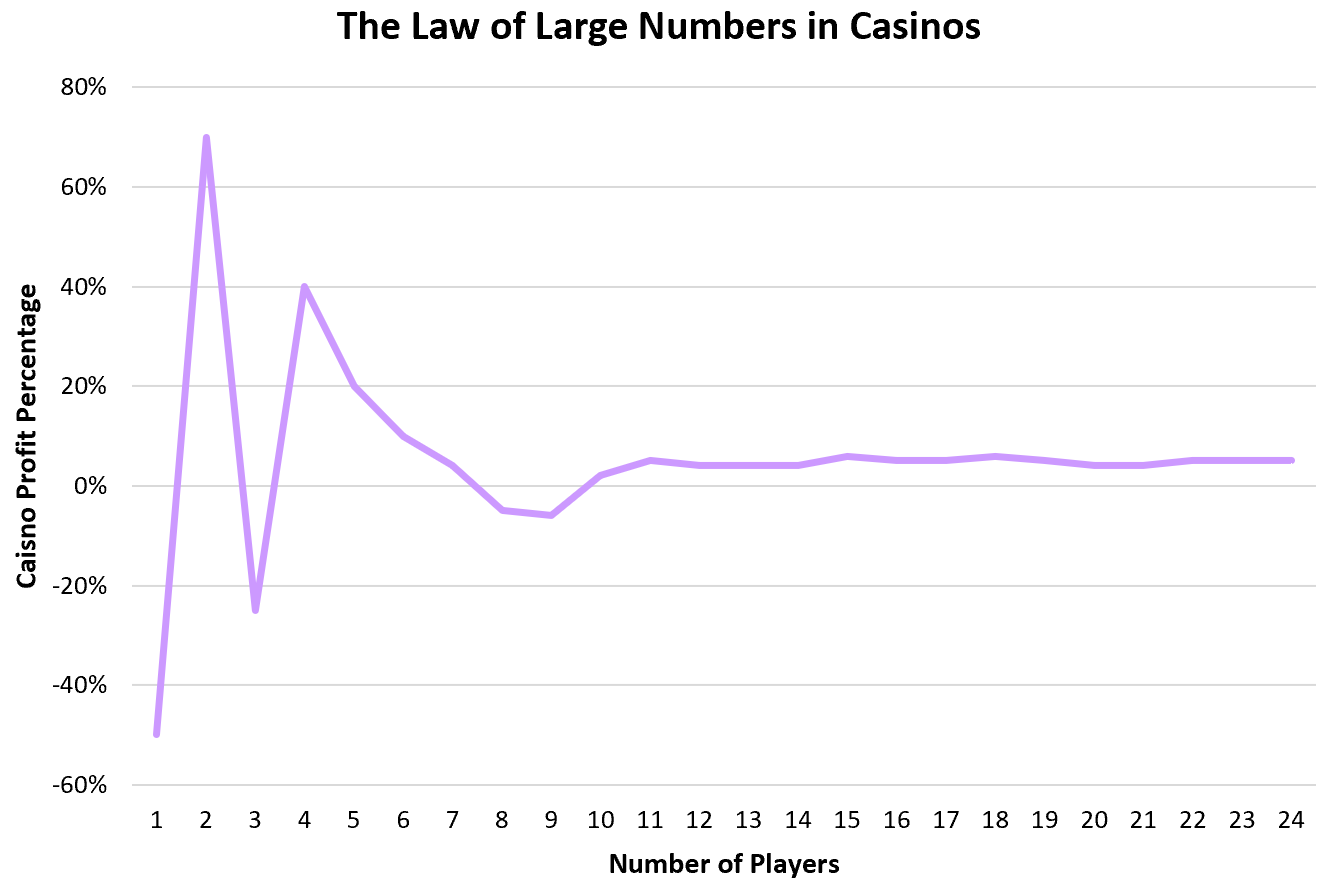
Казино полагаются на закон больших чисел для надежного получения прибыли. В большинстве игр казино выигрывает примерно в 51-55% случаев. Это означает, что отдельным людям может повезти и время от времени выиграть приличную сумму, но из десятков тысяч отдельных игроков казино выиграет ожидаемые 51-55% случаев.
Например, Джессика могла бы сыграть несколько игр в казино и выиграть 50 долларов.
Майк также мог сыграть несколько игр и проиграть 70 долларов.
Джон мог сыграть несколько игр и выиграть 25 долларов.
Сьюзен могла сыграть несколько игр и проиграть 40 долларов.
Некоторые игроки выиграют деньги, а другие проиграют, но благодаря тому, как устроены игры, казино могут быть уверены, что они выиграют у тысяч людей.
Закон больших чисел в страховании
Страховые компании также полагаются на закон больших чисел, чтобы оставаться прибыльными.
Основная идея заключается в том, что тысячи страховых компаний могут обеспечить страхование людей, которые ежемесячно платят определенную премию, и что лишь небольшой процент людей, которых они застрахуют, действительно будет нуждаться в использовании страховки для оплаты крупных непредвиденных расходов.
Например, каждый из 1000 человек может платить по 1000 долларов в год за страхование, что принесет страховой компании прибыль в размере 1 000 000 долларов.
Однако каждому из 90 человек может потребоваться получить от страховой компании по 10 000 долларов США для покрытия непредвиденных расходов, связанных с различными несчастными случаями, что приведет к убыткам страховой компании в размере 900 000 долларов США.
В итоге страховая компания получает прибыль в размере $1 000 000 – $900 000 = $100 000 .
Это означает, что страховая компания может рассчитывать на получение довольно предсказуемой прибыли в среднем от тысяч людей.
Обратите внимание, что эта экономическая модель работает, поскольку страховая компания страхует большое количество людей . Если бы они застраховали только 10 человек, это было бы слишком рискованно, потому что большие неожиданные расходы могли бы уничтожить бизнес.
Таким образом, страховые компании полагаются на закон больших чисел, чтобы прогнозировать свою прибыль.
Закон больших чисел в возобновляемой энергетике
Закон больших чисел также используется компаниями, занимающимися возобновляемой энергетикой.
Основная идея заключается в том, что ветряные турбины и солнечные панели могут питать генераторы для производства электроэнергии в различных частях бизнеса. Однако снаружи нет ветра и солнца, а это означает, что ветряные турбины и солнечные панели не всегда могут надежно обеспечивать электрогенераторы.
Способ, которым компании, занимающиеся возобновляемой энергетикой, решают эту проблему, заключается в подключении десятков тысяч ветряных турбин или солнечных панелей к единой электросети, что значительно повышает вероятность того, что эти источники энергии будут производить надежное количество энергии. энергия для сети.
Также гораздо легче предсказать, сколько энергии будет производиться этими источниками энергии, поскольку инженеры могут просто взять ожидаемое среднее значение для десятков тысяч ветряных турбин или солнечных панелей.
Подробное объяснение этого явления можно найти в статье Scientific American .