Распределение парето
В этой статье объясняется, что такое распределение Парето в статистике и для чего оно используется. Вы также сможете увидеть график распределения Парето и свойства этого типа распределения вероятностей.
Что такое распределение Парето?
Распределение Парето — это непрерывное распределение вероятностей, используемое в статистике для моделирования принципа Парето. Следовательно, распределение Парето — это распределение вероятностей, имеющее несколько значений, вероятность появления которых значительно выше остальных значений.
Помните, что закон Парето, также называемый правилом 80-20, представляет собой статистический принцип, который гласит, что большая часть причин явления связана с небольшой частью населения.
Распределение Парето имеет два характерных параметра: параметр масштаба x m и параметр формы α.
Первоначально распределение Парето использовалось для описания распределения богатства среди населения, поскольку большая его часть принадлежала небольшой части населения. Но в настоящее время распределение Парето имеет множество применений, например, в контроле качества, в экономике, в науке, в социальной сфере и т. д.
Распределение Парето названо в честь экономиста Вильфредо Парето, который сформулировал это распределение. Однако наиболее известен он благодаря диаграмме Парето.
Таблица распределения Парето
Теперь, когда мы знаем определение распределения Парето, давайте посмотрим на несколько примеров распределений Парето, представленных графически.
Итак, ниже вы можете увидеть, как выглядит график функции плотности распределения Парето в зависимости от его характерных значений:
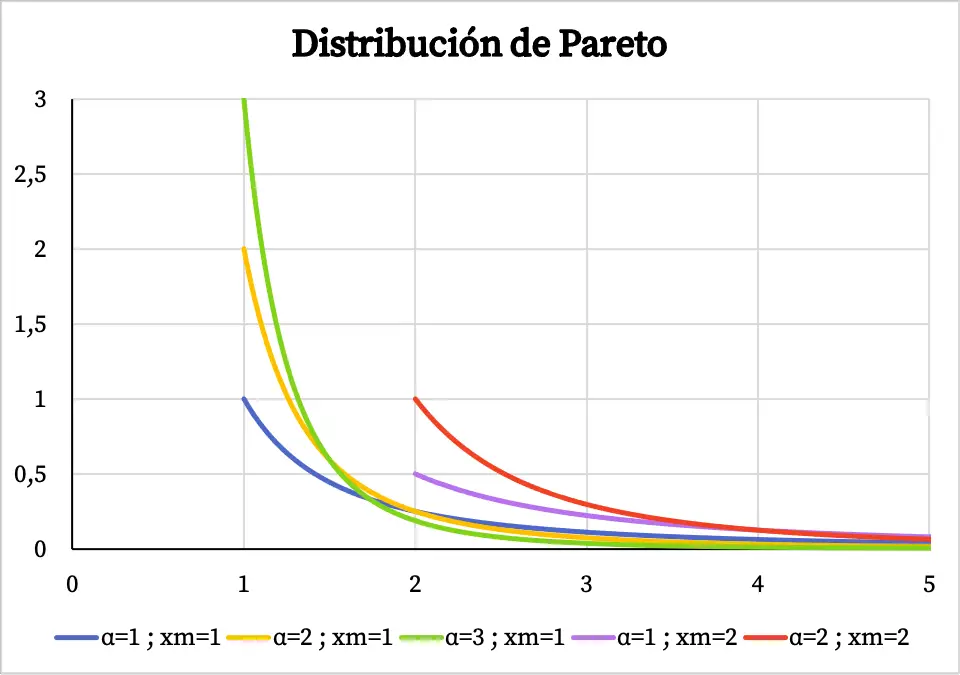
Обратите внимание, что область распределения Парето простирается от значения x m до +∞, поэтому функция плотности не существует до значения x m .
С другой стороны, график кумулятивной функции вероятности распределения Парето выглядит следующим образом:
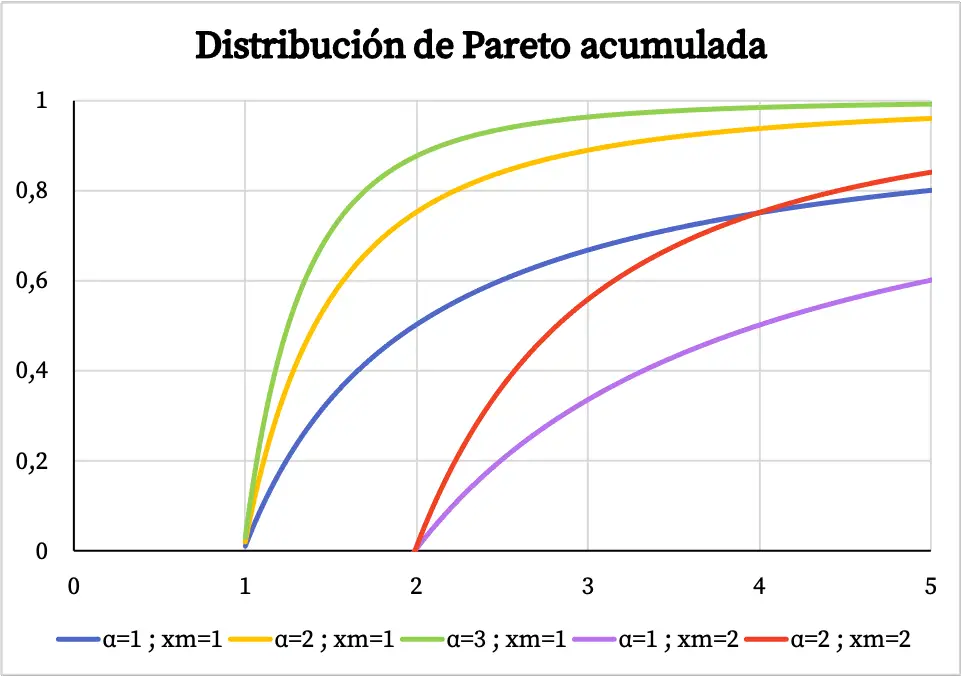
Характеристики распределения Парето
Ниже приведены наиболее важные характеристики распределения Парето, связанные с теорией вероятностей и статистикой.
- Распределение Парето имеет два характерных параметра, определяющих его кривую: параметр масштаба x m и параметр формы α.
- Область распределения Парето состоит из всех действительных чисел от параметра масштаба до плюс бесконечности.
- Если α больше 1, среднее значение распределения Парето равно произведению α, умноженного на x m , и α минус 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=»Rendered by QuickLaTeX.com» height=»34″ width=»214″ style=»vertical-align: -12px;»></p>
</p>
<ul>
<li> Дисперсия распределения Парето зависит от двух характерных параметров распределения и рассчитывается по следующей формуле:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
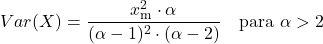
- Мода распределения Парето эквивалентна параметру масштаба x m распределения.
- Формула функции плотности распределения Парето:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- Аналогично, формула для кумулятивной функции вероятности распределения Парето:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- Коэффициент асимметрии распределения Парето зависит только от параметра формы α и его выражение имеет вид:
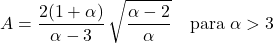
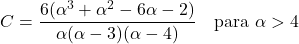
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше