Разница между значениями z и значениями p в статистике
Два термина, которые студенты часто путают в статистике, — это z-значения и p-значения .
Чтобы понять разницу между этими терминами, полезно разобраться с z-тестами .
Существует два распространенных типа z-тестов:
- Одновыборочный z-тест : используется для проверки того, соответствует ли среднее значение совокупности определенному значению.
- Z-тест для двух выборок : используется для проверки равенства двух средних значений генеральной совокупности.
Для выполнения каждого теста мы используем следующие шаги:
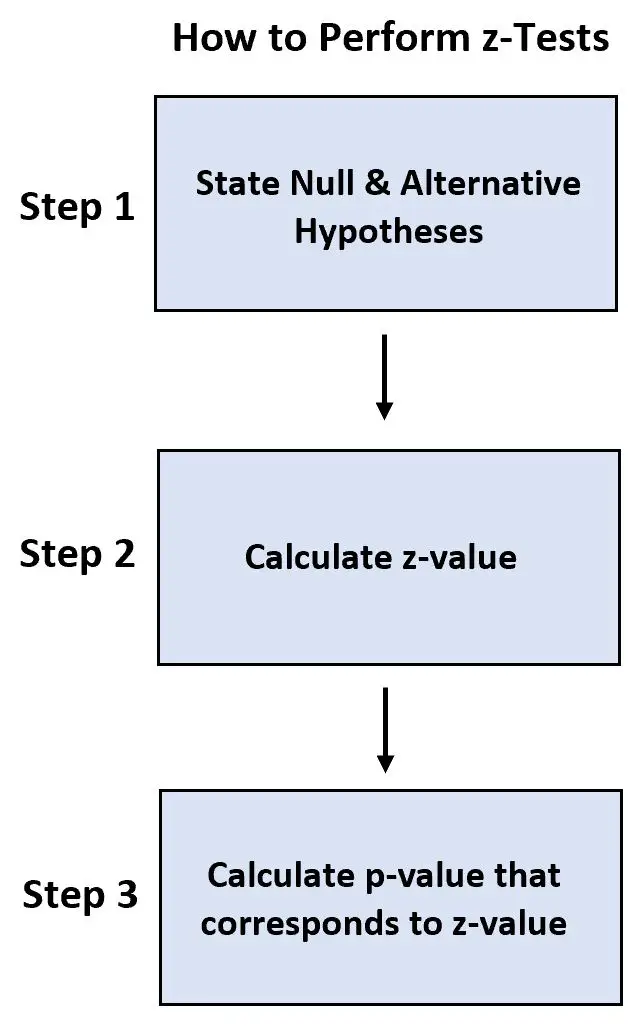
- Шаг 1: Сформулируйте нулевую и альтернативную гипотезы.
- Шаг 2: Рассчитайте значение z.
- Шаг 3: Рассчитайте значение p, соответствующее значению z.
Для каждого теста значение z — это способ количественной оценки разницы между средними значениями генеральной совокупности, а значение p — это вероятность получения значения z с абсолютным значением, по крайней мере, таким же большим, какое мы фактически наблюдали в «выборке». данные, если нулевая гипотеза действительно верна.
Если значение p меньше определенного значения (например, 0,05), мы отвергаем нулевую гипотезу теста.
Для каждого типа z-теста нас интересует значение p , и мы просто используем значение z в качестве промежуточного шага для расчета значения p.
В следующем примере показано, как вычислить и интерпретировать значение z и соответствующее значение p для z-критерия с двумя выборками.
Пример: расчет и интерпретация значений Z и значений P
Предположим, что уровни IQ людей из двух разных городов нормально распределены, каждый со стандартным отклонением населения 15.
Ученый хочет знать, различается ли средний уровень IQ жителей городов А и Б. Поэтому она выбирает простую случайную выборку из 20 человек из каждого города и записывает их уровни IQ:
Город А : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114.
Город Б : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133.
Вот как выполнить z-тест с двумя выборками, используя эти данные:
Шаг 1: Сформулируйте нулевую и альтернативную гипотезы.
Сначала сформулируем нулевую и альтернативную гипотезы:
- H 0 : μ 1 = μ 2 (два средних значения совокупности равны)
- H 1 : μ 1 ≠ μ 2 (два средних значения совокупности не равны)
Шаг 2: Рассчитайте значение z.
Далее мы выполним z-тест для двух выборок в Excel, используя эти данные, и обнаружим, что значение z равно -1,71817 .
Шаг 3: Рассчитайте значение p.
Мы можем использовать калькулятор Z-оценки для значения P, чтобы определить, что значение p, соответствующее значению az -1,71817, составляет 0,08577.
Поскольку это значение p не меньше 0,05, у нас нет достаточных доказательств, чтобы отвергнуть нулевую гипотезу.
Таким образом, мы приходим к выводу, что средний уровень IQ существенно не отличается между двумя городами.
Обратите внимание, что мы просто использовали значение z в качестве промежуточного шага для расчета значения p.
Значение p — это истинное значение, которое нас интересовало, но сначала нам нужно было вычислить значение z.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять z-тесты с использованием различного статистического программного обеспечения:
Как выполнить Z-тесты в Excel
Как выполнить Z-тесты в R
Как выполнить Z-тесты в Python
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше