Как извлечь остатки из функции lm() в r
Вы можете использовать следующий синтаксис для извлечения остатков из функции lm() в R:
fit$residuals
В этом примере предполагается, что мы использовали функцию lm() для подбора модели линейной регрессии и назвали результаты fit .
В следующем примере показано, как использовать этот синтаксис на практике.
Связанный: Как извлечь R-квадрат из функции lm() в R
Пример: как извлечь остатки из lm() в R
Предположим, у нас есть следующий кадр данных в R, который содержит информацию о сыгранных минутах, общем количестве нарушений и общем количестве очков, набранных 10 баскетболистами:
#create data frame df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40), fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1), points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30)) #view data frame df minutes fouls points 1 5 5 6 2 10 5 8 3 13 3 8 4 14 4 7 5 20 2 14 6 22 1 10 7 26 3 22 8 34 2 24 9 38 1 28 10 40 1 30
Предположим, мы хотим подогнать следующую модель множественной линейной регрессии:
очки = β 0 + β 1 (минуты) + β 2 (нарушения)
Мы можем использовать функцию lm() , чтобы соответствовать этой модели регрессии:
#fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)
Затем мы можем ввести fit$residuals , чтобы извлечь остатки из модели:
#extract residuals from model
fit$residuals
1 2 3 4 5 6 7
2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786
8 9 10
-1.7048752 0.5692404 0.6144057
Поскольку всего в нашей базе данных было 10 наблюдений, то и остатков осталось 10 – по одному на каждое наблюдение.
Например:
- Первое наблюдение имеет остаток 2089 .
- Второе наблюдение имеет остаток -0,798 .
- Третье наблюдение имеет остаток 0,637 .
И так далее.
Затем мы можем создать график остатков в зависимости от подобранных значений, если захотим:
#store residuals in variable
res <- fit$residuals
#produce residual vs. fitted plot
plot(fitted(fit), res)
#add a horizontal line at 0
abline(0,0)
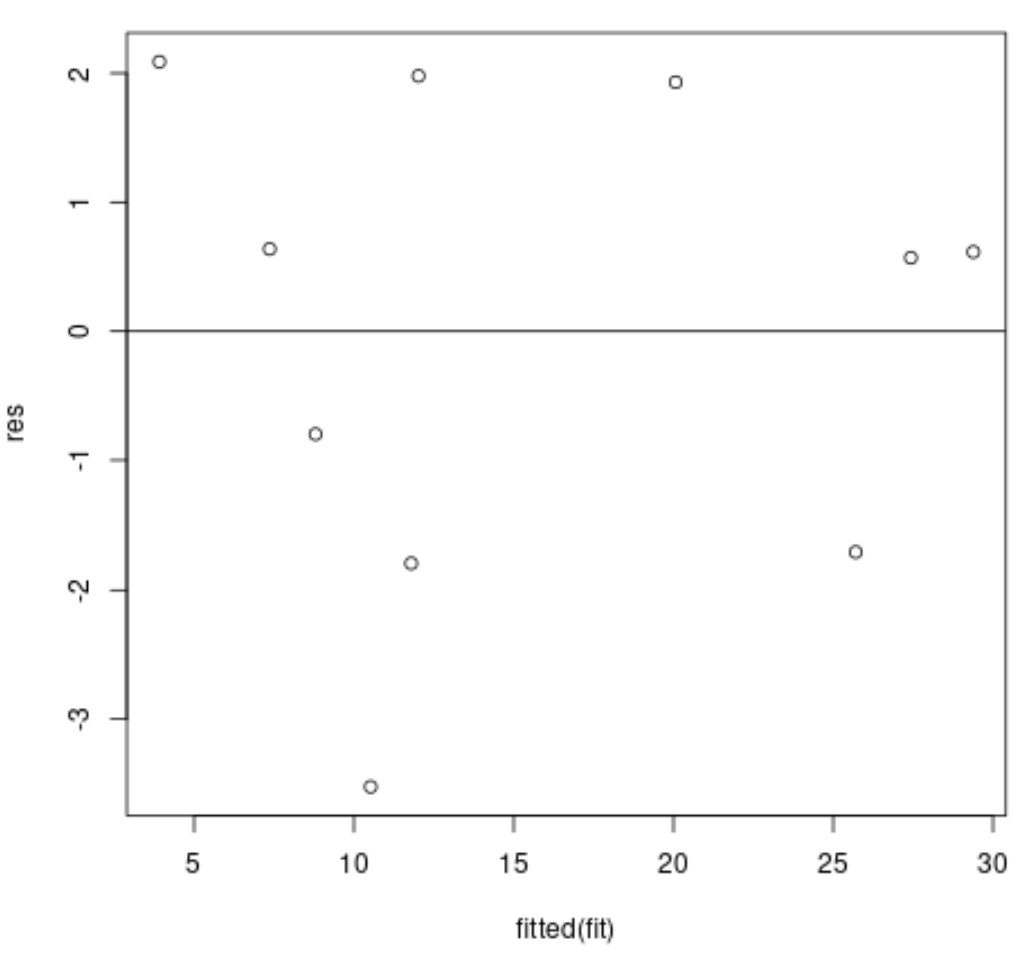
По оси X отображаются подобранные значения, а по оси Y — остатки.
В идеале остатки должны быть случайным образом разбросаны вокруг нуля без четкой закономерности, чтобы гарантировать выполнение предположения о гомоскедастичности .
На приведенном выше графике остатков мы видим, что остатки кажутся случайным образом разбросанными вокруг нуля без четкой закономерности, а это означает, что предположение о гомоскедастичности, вероятно, выполняется.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как создать остаточный график в R